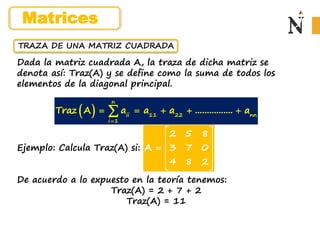
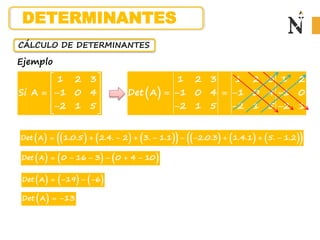
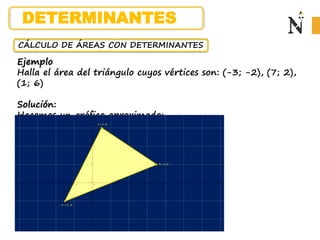
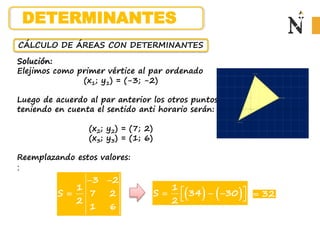
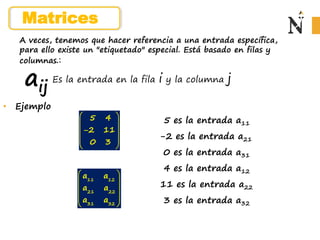
El documento describe cómo un candidato contrató una empresa de relaciones públicas para dar a conocer sus propuestas durante las elecciones municipales en dos distritos a través de llamadas telefónicas, volantes y cartas. Se proporcionan los costos de cada método de contacto en una matriz, así como el número de contactos establecidos en cada distrito en otra matriz. Se piden calcular la cantidad total gastada en cada distrito.

1. MATEMÁTICA BÁSICA
Matrices y Determinantes

2. 2
Para las elecciones municipales de Trujillo, un candidato contrato los servicios
de una empresa de relaciones públicas para dar a conocer sus propuestas y
ganar las elecciones, mediante tres formas: por teléfono, volantes a la casa y
mediante cartas. El costo por cada contacto establecido se obtiene mediante
la matriz:
El número de contactos establecidos en dos distritos, se calcula mediante la
matriz:
a) Halle la cantidad total que se gastó en la ciudad A
b) Halle la cantidad total que se gastó en la ciudad B
$ 0, 40
$ 0,75
$ 0, 25
 
 
 
 
 
Costos por contrato
TELEFONO
VOLANTE
CARTA
200 150 100
140 300 120
 
 
 
TELEFONO VOLANTE CARTA
distrito A
distrito B
CASO APLICATIVO

3. Al finalizar la sesión de aprendizaje,
el estudiante resuelve e interpreta
problemas aplicativos en una hoja
de trabajo vinculados a su carrera
haciendo uso de las operaciones
con Matrices y Determinantes
LOGRO DE LA SESIÓN

4. • Operaciones básicas
• Ecuaciones

5. • MATRICES
• Definición
• Clases
• Operaciones con Matrices
• Problemas con Matrices
• DETERMINANTES
• Definición
• Operaciones

6. Matrices y Determinantes
Las operaciones que uno pueda realizar con la información
depende del campo de aplicación en donde se empleen
matrices; esos campos pueden ser: economía, teoría de juegos,
genética, sociología, estudios sobre flujo de tránsito, modelos de
crecimiento de una población, manejo de información secreta,
etc.
¿EN QUÉ SE APLICA?

7. 7
Matrices
Al realizar el inventario en los tres almacenes de una tienda se obtuvo:
 Almacén 1: 12 computadoras, 8 impresoras
y 5 escáneres.
 Almacén 2: 20 computadoras, 18 impresoras
y 9 escáneres.
 Almacén 3: 2 computadoras, 3 impresoras
y 15 escáneres.
¿Cuántos artículos de cada tipo hay en la tienda?
Organizamos los datos, en filas y
columnas formando un arreglo
rectangular.
La fila indica el almacén y la columna
el artículo.
C I E
Almacén 1 12 8 5
Almacén 2 20 18 9
Almacén 3 2 3 15
Total 34 29 29
En total hay 34 computadoras, 29 impresoras y 29 escáneres.

8. • Se denomina matriz a un arreglo rectangular ordenado de
elementos dispuestos en filas y columnas, que se encierran
entre corchetes o paréntesis. Para representar a una matriz
se utilizan letras mayúsculas. Veamos por ejemplo:
DEFINICIÓN
1 2 3 5
A 4 1 0 9
6 8 1 3
 
 
 
 
 

 
FILA
C
O
L
U
M
N
A
Matrices

9. Forma general de una matriz
Sea A una matriz de m filas y n columnas, es decir A es de orden
m x n, luego ésta se representa así:
a23 representa al elemento que está en la segunda fila (2) y en la
tercera columna (3).
11 12 13 1n
21 22 23 2n
31 32 33 3n
m1 m2 m3 mn
a a a ......... a
a a a ......... a
a a a ......... a
A
..... ...... ....... ......... ......
..... ...... ....... ......... ......
a a a ......... a
 
 
 
 
 

 
 
 
 
 
a23
Matrices

10. • Ejemplo
A veces, tenemos que hacer referencia a una entrada específica,
para ello existe un "etiquetado" especial. Está basado en filas y
columnas.:
Es la entrada en la fila i y la columna j
aij
5 4
2 11
0 3
 
 

 
 
 
11 12
21 22
31 32
a a
a a
a a
 
 
 
 
 
5 es la entrada a11
-2 es la entrada a21
0 es la entrada a31
4 es la entrada a12
11 es la entrada a22
3 es la entrada a32
Matrices

11. 3 8 3 8
A 2 a ; B 2 7
b 6 5 6
   
   
 
   
   
   
• Igualdad de matrices
• Dos o más matrices son iguales si y sólo si son del mismo
orden, siendo todos sus elementos correspondientes iguales
Para que las matrices A y B sean iguales, se tiene que
cumplir que a = 7 y b = 5.
Matrices

12. 01. Escribe una matriz 3x1 tal que aij = i2 - j
02. Escribe una matriz 3x3 tal que aij = 2i - 3j
03. Escribe una matriz 4x3 tal que
04. Dadas las matrices:
A = (aij)2x2 / aij = i - 2j
Determina los valores de x e y, si A = B
EJERCICIOS
i j
i j ; si i j
a
i j ; si i j
  

 
 


y x x 3y
B
0 2
 
 
  

 
 
Matrices

13. CLASES DE MATRICES
Atendiendo a la forma:
Matriz
fila
Matriz
columna
Matriz
cuadrada
Matriz
rectangular
Tiene una fila
y n columnas
Tiene m filas
y una columna
Tiene el mismo
número de filas
y columnas
Tiene distinto
número de filas
y columnas
Ejemplo:
Matriz de 1x4
Ejemplo:
Matriz de 3x1
Ejemplo:
Matriz de 3x3
Ejemplo:
Matriz de 3x2
F 1 2 3 4
 
  
1
C 2
3
 
 
  
 
 
1 2
B 3 4
5 6
 
 
  
 
 
1 2 3
A 4 5 6
7 8 9
 
 
  
 
 
Matrices

14. CLASES DE MATRICES
Atendiendo a los elementos:
Matriz
nula
Matriz
diagonal
Matriz
escalar
Matriz
unidad
Tiene todos sus
elementos
iguales a cero.
Todos los
elementos que no
están en la
diagonal principal
son 0.
Matriz diagonal en
la que todos los
elementos de la
diagonal principal
son iguales.
Matriz escalar en
la que todos los
elementos de la
diagonal principal
son 1.
Ejemplo: Ejemplo: Ejemplo: Ejemplo:
1 0 0
D 0 6 0
0 0 3
 
 
  
 
 
0 0 0
N
0 0 0
 
  
 
 
3 0 0
E 0 3 0
0 0 3
 
 
  
 
 
3
1 0 0
I 0 1 0
0 0 1
 
 
  
 
 
Matrices

15. CLASES DE MATRICES
Atendiendo a los elementos:
Matriz
triangular
Matriz cuadrada en la que
todos los elementos situados
por debajo (o por encima) de la
diagonal principal son cero.
Ejemplos:
1 2 3 1 0 0
A 0 6 4 ; B 2 6 0
0 0 5 3 4 5
   
   
 
   
   
   
Matrices

16. TRANSPUESTA DE UNA MATRIZ
Se llama traspuesta de A, y se representa por AT, a aquella
matriz construida a partir de la matriz A intercambiando sus
filas por sus respectivas columnas. La primera fila de A es la
primera columna de At, la segunda fila de A es la segunda
columna de AT, etc. De la definición se deduce que si A es de
orden m x n, entonces At es de orden n x m.
Así por ejemplo:
T
ij ji
mxn nxm
Si : A a A a
   
  
   
T
2 3 7
A
1 5 4
 
  
 

 
2 1
A 3 5
7 4
 

 
  
 
 
su transpuesta será:
Matrices

17. 05. Determina las transpuestas de las siguientes matrices:
06. Dada la matriz cuadrada de orden 3 tal que aij = 3i – 2j.
Encuentra su transpuesta.
EJERCICIOS
2 3 1 3 0
A ; B
1 0 9 2 1
   

 
   

   
   
Matrices

18. OPERACIONES CON MATRICES
Adición y/o sustracción de matrices
La suma (diferencia) de dos matrices A = (aij), B =(bij) de la
misma dimensión, es otra matriz S = (sij) de la misma
dimensión que los sumandos y con término genérico
sij = aij ± bij
Así por ejemplo:
Halla A + B y A – B dadas las matrices:
1 2 3 3 2 5
A ; B
0 2 1 1 3 4
   
 
 
   
   

   
Matrices

19. OPERACIONES CON MATRICES
Propiedades de la suma de matrices
P1. A + (B + C) = (A + B) + C (propiedad asociativa)
P2. A + B = B + A (propiedad conmutativa)
P3. A + 0 = A (0 es la matriz nula)
P4. La matriz –A, que se obtiene cambiando de signo todos
los elementos de A, recibe el nombre de matriz opuesta de A,
ya que A + (–A) = 0.
Matrices

20. OPERACIONES CON MATRICES
Producto de un número por una matriz
El producto de una matriz A = (aij) por un número real k es
otra matriz B = (bij) de la misma dimensión que A y tal que
cada elemento bij de B se obtiene multiplicando aij por k, es
decir:
bij = k·aij
Así por ejemplo:
Efectúa 3A, si A es:
2 1 0
A
3 4 5
 

  
 

 
Matrices

21. OPERACIONES CON MATRICES
Propiedades del producto de una matriz por un número
P1. k (A + B) = k A + k B (propiedad distributiva)
P2. (k + h)A = k A + h A (propiedad distributiva)
P3. k [h A] = (k h) A (propiedad asociativa)
P4. 1·A = A (elemento unidad)
P5. Si A + C = B + C → A = B.
Matrices

22. Producto de dos matrices
Ejemplo:
Calcula A.B, si:
Solución:
3 0 4
A 1 2 y B
5 2 3
 

 
   
  
 
 
   
   
   
3
1 2 . 1 3 2 5 7
5
3 0 4 0
A.B 1 2 . 1 2 . 1 0 2 2 4
5 2 3 2
4
1 2 . 1 4 2 3 10
3
  

     
  
 
  
 

   
 
   
      
   

   
 
   

   
  
 
   
 
 
  
 

A.B 7 4 10
 
 
 
Matrices

23. OPERACIONES CON MATRICES
Propiedades del producto de matrices
P1. A·(B·C) = (A·B)·C
P2. El producto de matrices en general no es conmutativo.
P3. Si A es una matriz cuadrada de orden n se tiene
A·In = In·A = A
P4. Dada una matriz cuadrada A de orden n, no siempre
existe otra matriz B tal que A·B = B·A = In. Si existe dicha
matriz B, se dice que es la matriz inversa de A y se
representa por A–1 .
5. El producto de matrices es distributivo respecto de la
suma de matrices, es decir: A·(B + C) = A·B + A·C
Matrices

24. 07. Dadas las matrices:
Determina la suma de los elementos de la matriz A + C, si A = B.
08. Sean las matrices:
Halla las matrices:
i. A + B
ii. 3A – 2B
iii. A + 2B – 3I
24
EJERCICIOS
2x 1 y 5 y 2 x y x
A ; B ; C
3 y 2 x 1 2 3 4
     
  
  
     
 
     
     
2
2 5 5 9 1 0
A ; B ; I
4 1 7 4 0 1
     

  
     

     
     
Matrices

25. TRAZA DE UNA MATRIZ CUADRADA
Dada la matriz cuadrada A, la traza de dicha matriz se
denota así: Traz(A) y se define como la suma de todos los
elementos de la diagonal principal.
Ejemplo: Calcula Traz(A) si:
De acuerdo a lo expuesto en la teoría tenemos:
Traz(A) = 2 + 7 + 2
Traz(A) = 11
2 5 8
A 3 7 0
4 8 2
 
 
  
 
 
 
n
ii 11 22 nn
i 1
Traz A a a a ................ a

    

Matrices

26. TRAZA DE UNA MATRIZ CUADRADA
Propiedades de la traza
P1. Traz (A + B) = Traz (A) + Traz (B)
P2. Traz (k.A) = k.Traz (A)
P3. Traz (A.B) = Traz (B.A)
Matrices

27. EJERCICIOS
01. Dada la matriz:
Calcula el valor de E = a12 + a2
12 + a33
02. Calcula el valor de P = 4x + 2y – z, si:
03. Calcula la traza de C, si:
2 3 1
A 0 2 4
3 0 5
 
 
 
 
 
 

 
2x 1 3 3y 6y
A ; B A B
4 1 2z 1
   

   
   
  
   
   
1 4 3 2
A ; B C 2A 3B
2 5 2 1
   
    
   
 
   
   
Matrices

28. EJERCICIOS
04. Dada la matriz:
Determina 2AT
3 2
A 1 4
7 6
 
 
  
 
 
Matrices

29. CONTENIDO
1. DEFINICIÓN
2. CÁLCULO DE DETERMINANTES
• Orden 1
• Orden 2
• Orden 3
3. CÁLCULO DE ÁREAS CON DETERMINANTES
4. PROBLEMAS QUE SE RESUELVEN USANDO DETERMINANTES
DETERMINANTES

30. DEFINICIÓN
El determinante es una función que aplicada a una matriz
cuadrada, nos proporciona un número real.
Su notación es la siguiente:
 
Det A A

CÁLCULO DE DETERMINANTES
Determinante de una matriz de orden 1
Sea A una matriz de orden uno, es decir su
determinante se denota así:
11
A a
 
  
  11 11
Det A a a
 
DETERMINANTES

31. CÁLCULO DE DETERMINANTES
Determinante de una matriz de orden 2
Sea A una matriz de orden dos, su determinante se define
como la diferencia del producto de los elementos de la diagonal
principal con el producto de los elementos de la diagonal
secundaria. Esto es:
 
11 12 11 12
21 22 21 22
a a a a
Si A Det A
a a a a
 
  
 
 
 
Ejemplo
5 2
Si A
7 9
 

  
 
 
 
5 2
Det A
7 9

 59
 
11 22 21 12
a .a a .a
 
       
5 . 9 7 . 2
  
DETERMINANTES

32. CÁLCULO DE DETERMINANTES
Determinante de una matriz de orden 3
El determinante de orden 3 se obtiene por la llamada regla de
SARRUS. Consiste en repetir las dos primeras columnas a
continuación de la matriz, sumar los productos de las
diagonales principales y restar los productos de las diagonales
Secundarias.
 
11 12 13 11 12 13
21 22 23 21 22 23
31 32 33 31 32 33
a a a a a a
Si A a a a Det A a a a
a a a a a a
 
 
  
 
 
 
11 12
21 22
31 32
a a
a a
a a
     
11 22 33 12 23 31 13 21 32 31 22 13 32 23 11 33 21 12
Det A a .a .a a .a .a a .a .a a .a .a a .a .a a .a .a
     
DETERMINANTES

33. CÁLCULO DE DETERMINANTES
Ejemplo
1 2 3
Si A 1 0 4
2 1 5
 
 
 
 
 

 
 
1 2 3 1 2 3 1 2
Det A 1 0 4 1 0 4 1 0
2 1 5 2 1 5 2 1
    
  
       
       
 
Det A 1.0.5 2.4. 2 3. 1.1 2.0.3 1.4.1 5. 1.2
         
     
Det A 0 16 3 0 4 10
     
     
Det A 19 6
   
 
Det A 13
 
DETERMINANTES

34. CÁLCULO DE ÁREAS CON DETERMINANTES
Sea A1 , A2 , A3 , ........, An un polígono de “n” lados cuyos
vértices nombrados en sentido antihorario, tiene como
coordenadas : A1(x1; y1), A2(x2; y2), A3(x3; y3), ……… An(xn; yn).
Entonces el área de la región poligonal S correspondiente, se
puede calcular mediante la expresión:
1 1
2 2
n n
x y
x y
1
.... ....
S
2
.... ....
x y

Llamada también formula determinante de Gauss
DETERMINANTES

35. CÁLCULO DE ÁREAS CON DETERMINANTES
Ejemplo
Halla el área del triángulo cuyos vértices son: (-3; -2), (7; 2),
(1; 6)
Solución:
Hacemos un gráfico aproximado:
DETERMINANTES

36. CÁLCULO DE ÁREAS CON DETERMINANTES
Solución:
Elejimos como primer vértice al par ordenado
(x1; y1) = (-3; -2)
Luego de acuerdo al par anterior los otros puntos,
teniendo en cuenta el sentido anti horario serán:
(x2; y2) = (7; 2)
(x3; y3) = (1; 6)
Reemplazando estos valores:
:
3 2
1
S 7 2
2
1 6
 
    
1
S 34 30
2
 
  
  32

DETERMINANTES

37. SOLUCIÓN DEL CASO

38. EVALUACIÓN
Trabajo de Equipo: en grupos de 4 estudiantes
Resuelven los ejercicios y problemas aplicativos sobre
Matrices y Determinantes, propuestos en la hoja de
trabajo.

39. APLICACIÓN
La compañía de dulces “QUE RICO” consta de dos locales, uno en Comas y otro
en Chorrillos. ”QUE RICO” recibió un pedido por 500 tortas y 1000 piononos. La
gerencia ha decidido elaborar 300 tortas y 700 piononos en su local de Comas y
el resto del pedido en Chorrillos. Cada torta requiere 300 gramos de harina y 150
gramos de azúcar, mientras que cada pionono requiere 100 gramos de harina y
30 gramos de azúcar. La harina cuesta 2 soles el kilogramo y el azúcar 3,50
soles el kilogramo.
• Haciendo uso de operaciones matriciales, encuentre la matriz que contenga la
cantidad de insumos (harina y azúcar) que será necesario utilizar en cada
local para cumplir con el pedido.
• Haciendo uso de operaciones matriciales, encuentre la matriz que contenga el
gasto, en soles, que cada local debe realizar para la compra de los insumos.

40. BIBLIOGRAFÍA: E-BOOKS