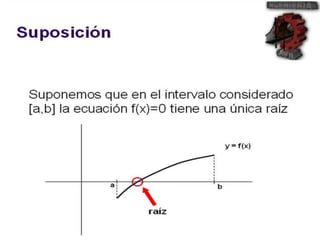
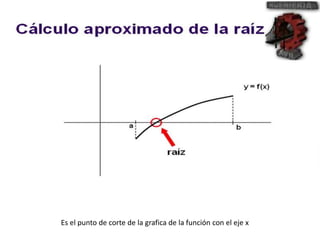
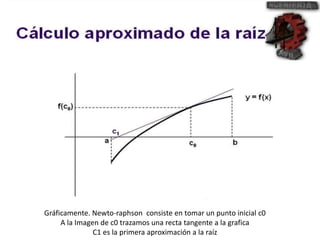
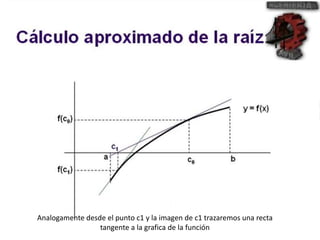
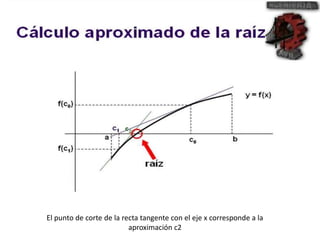
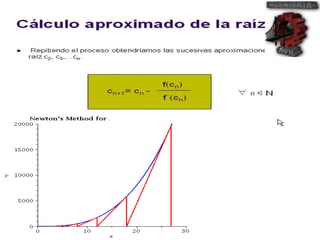
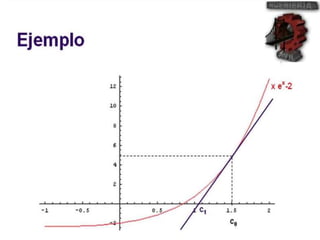
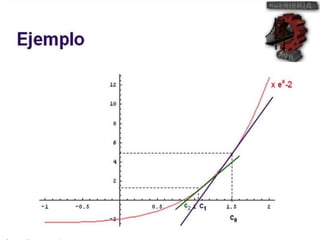
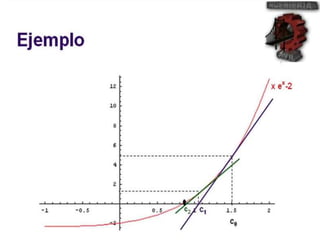
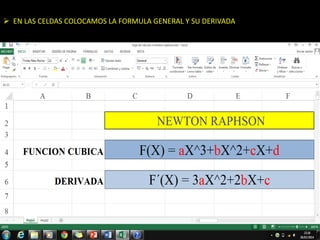
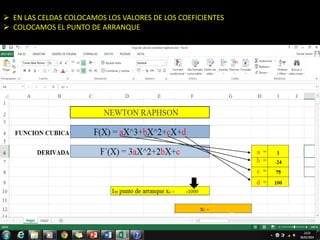
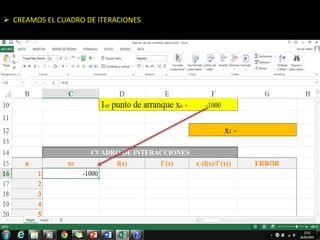
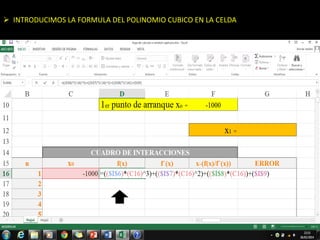
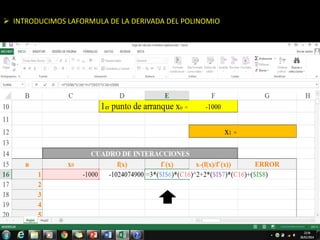
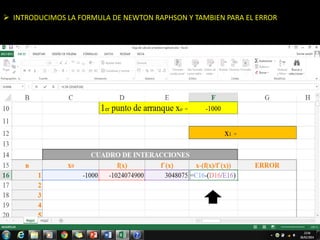
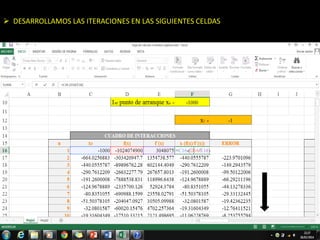
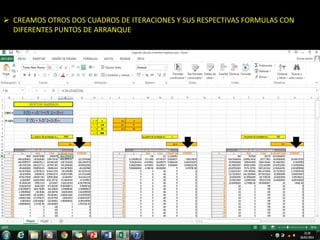
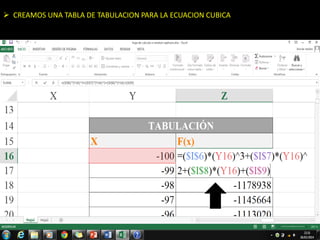
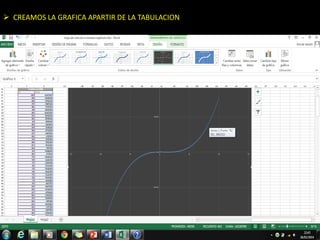
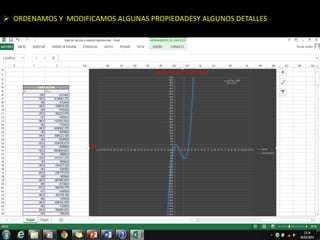
El método de Newton-Raphson se utiliza para encontrar las raíces de ecuaciones a través de aproximaciones iterativas, requiriendo la derivada de la función y un valor inicial. Este método es exclusivo para funciones de una sola variable y tiene aplicaciones en sistemas multivariables y optimización. Además, se puede implementar en Excel para calcular raíces de polinomios, utilizando fórmulas en celdas y creando iteraciones gráficas.

1. METODO DE
NEWTON
RAPHSON
Zegarra Vargas kevi ney antonio

2. Método de Newton Raphson para raíces
múltiples
El Método de Newton-Raphson es ampliamente utilizado para encontrar las
raíces de la ecuación f(x)=0, ya que converge rápidamente, se debe conocer
la derivada de f(x) y se necesita una aproximación inicial a la raíz.
Permite aproximar las primeras N iteraciones en el método de Newton-
Raphson aplicado a la función f tomando como aproximación inicial c0
Nótese que el método descrito es de aplicación exclusiva para funciones de
una sola variable con forma analítica o implícita conocible. Existen variantes
del método aplicables a sistemas discretos que permiten estimar las raíces
de la tendencia, así como algoritmos que extienden el método de Newton a
sistemas multivariables, sistemas de ecuaciones, etc.

3. -Encontrar aproximaciones de los
ceros o raíces de una función real.
También puede ser usado para
encontrar el máximo o mínimo de
una función, encontrando los ceros
de su primera derivada.

5. Es el punto de corte de la grafica de la función con el eje x

6. Gráficamente. Newto-raphson consiste en tomar un punto inicial c0
A la Imagen de c0 trazamos una recta tangente a la grafica
C1 es la primera aproximación a la raíz

7. Analogamente desde el punto c1 y la imagen de c1 trazaremos una recta
tangente a la grafica de la función

8. El punto de corte de la recta tangente con el eje x corresponde a la
aproximación c2

9. Analíticamente

11. Existe su 2da derivada y es continua
Pretendemos que las sucesivas aproximaciones se acerquen mas a la raíz. Y
asegurar la convergencia

16. LO QUE SABEMOS ES UNA GOTA DE
AGUA: LO QUE IGNORAMOS ES EL
OCEANO
ISSAC NEWTON

17. PROGRAMACION EN EXEL
 CON LA HOJA DE CALCULO DE EXEL SE PUEDE
HALLAR LAS RAICES DE UN POLINOMIO DE GRADO
3 HACIENDO USO DEL METODO DE NEWTON
RAPHSON
 TENIENDO EN CUENTA QUE LA HOJA DE CALCULO
DE EXEL ES UNA DE LAS MUCHAS HERRAMIENTAS
QUE PODEMOS HALLAR LAS RAICES

18.  EN LAS CELDAS COLOCAMOS LA FORMULA GENERAL Y SU DERIVADA

19.  EN LAS CELDAS COLOCAMOS LOS VALORES DE LOS COEFICIENTES
 COLOCAMOS EL PUNTO DE ARRANQUE

20.  CREAMOS EL CUADRO DE ITERACIONES

21.  INTRODUCIMOS LA FORMULA DEL POLINOMIO CUBICO EN LA CELDA

22.  INTRODUCIMOS LAFORMULA DE LA DERIVADA DEL POLINOMIO

23.  INTRODUCIMOS LA FORMULA DE NEWTON RAPHSON Y TAMBIEN PARA EL ERROR

24.  DESARROLLAMOS LAS ITERACIONES EN LAS SIGUIENTES CELDAS

25.  CREAMOS OTROS DOS CUADROS DE ITERACIONES Y SUS RESPECTIVAS FORMULAS CON
DIFERENTES PUNTOS DE ARRANQUE

26.  CREAMOS UNA TABLA DE TABULACION PARA LA ECUACION CUBICA

27.  CREAMOS LA GRAFICA APARTIR DE LA TABULACION

28.  ORDENAMOS Y MODIFICAMOS ALGUNAS PROPIEDADESY ALGUNOS DETALLES

30. VISTA GENERAL DE LA HOJA
DE CALCULO

31. GRACIAS