El documento explica la serie de Taylor como una herramienta matemática para aproximar funciones y calcular sus derivadas mediante polinomios. Se enfatiza su utilidad en ingeniería para evaluar funciones y sus derivadas con errores mínimos, utilizando aproximaciones sobre un punto de referencia. Además, se presentan ejemplos y se detalla el proceso para calcular la primera y segunda derivada sin necesidad de realizar derivadas tradicionales.

1. Facultad de Ingeniería Mecánica
Eléctrica, U.V., zona Xalapa
Métodos Numéricos
Serie de Taylor y la Valuación
Numérica de Derivadas
MC. Ing. Rafael Campillo Rodríguez
Introducción Aproximación a f’(x)
La Serie de Taylor Aproximación a f’’(x)

2. Introducción
Brook Taylor en su trabajo “Methodus
Incrementorum Directa et Inversa”
(1715) desarrolló lo que hoy se conoce
como cálculo de las diferencias finitas.
El mismo tratado contenía la famosa
fórmula conocida como el Teorema de
Taylor, cuya importancia sólo se
reconoció hasta 1772, cuando Joseph-
Louis Lagrange lo definió como “El
Brook Taylor,
fundamento principal del cálculo Reino Unido,
diferencial". 1685 - 1731

3. Introducción (Cont.)
La Serie de Taylor es una herramienta matemática que si
se usa apropiadamente facilita mucho los cálculos de
aproximación de funciones.
La idea fundamental detrás de la Serie de Taylor es la de
poder aproximar los valores de una función f(x) para
cualquier punto x, a partir de tener un punto de referencia
a situado a una distancia h del primero y todo esto a
partir de la creación de un “polinomio” basado en una
serie de potencias infinita para la cual sea posible de
manera sistemática calcular sus coeficientes.

4. Introducción (Cont.)
El polinomio: p(x) = a0 + a1 x + a2 x2 + .......... + an xn
en el que los coeficientes ai son constantes, se llama
“Polinomio de grado n”. En particular y=b+ax es un
polinomio de primer grado; de igual forma, y=c+bx+ax2
es un polinomio de segundo grado.
Los polinomios pueden considerarse las funciones más
sencillas de todas. Son funciones continuas para todo x y
tienen derivadas de cualquier orden.
Recordemos que, la derivada de un polinomio de grado n
es también un polinomio, de grado n-1; y sus derivadas
de orden n+1 y superiores, son nulas.

5. Introducción (Cont.)
El objetivo a lograr es encontrar el mejor polinomio que
permita aproximar cualquier valor de f(x) para una
función dada, con un valor casi exacto o teniendo un error
mínimo.
No todas las funciones pueden ser aproximadas usando un
polinomio y en particular por la Serie de Taylor, ya que
presentan alguna singularidad.
Sin embargo, la mayoría de las funciones obtenidas en los
casos prácticos dentro del área de la ingeniería, si son
aproximables por este método.

6. Introducción (Cont.)
Algunos ejemplos de series de funciones matemáticas
aproximables por la Serie de Taylor son,
x xn
Exponencial: e , x
n 0 n!
( 1)n 1
n
Logaritmo Natural: ln(1 x) x , para x 1
n 1 n
( 1)n 2n 1
Funciones Trigonométricas: sin( x) x , x
n 0 (2n 1)!
( 1)n 2n
cos( x) x , x
n 0 (2n)!

7. La Serie de Taylor
Comencemos el desarrollo de Taylor suponiendo lo
siguiente:
“Supongamos que f(x) es una función continua y
continuamente diferenciable en el intervalo [a,x].
Supondremos entonces que f ’(x), f ’’(x), f ’’’(x), … , f n(x)
están definidas para dicho intervalo”
Del “Teorema Fundamental del Cálculo” sabemos lo
siguiente:
a h a h
f '( x)dx f ( x) a
a

8. La Serie de Taylor (Cont.)
O bien,
a h
f '( x)dx f (a h) f ( xa)
a
De aquí que tengamos que:
a h
f (a h) f ( xa) f '( x)dx [1]
a

9. La Serie de Taylor (Cont.)
Ahora, supongamos que el valor de la derivada en
cualquier punto x, f’(x), permanece constante a lo largo
del intervalo [a,x] y con valor igual con f’(a), tendríamos
que se cumple que:
f '( x) f '(a)
Y entonces podríamos reescribir la ecuación [1], así:
a h
f (a h) f (a) f '(a)dx
a

10. La Serie de Taylor (Cont.)
Y como f’(a) es constante:
a h
f (a h) f (a) f '(a) dx
a
Resolviendo la integral:
f (a h) f (a) f '(a) h [2]

11. La Serie de Taylor (Cont.)
La ecuación resultante en [2] debe ser válida para
cualquier valor de x y también para cualquier función.
También sabemos que cualquier valor de x es igual con
a+h; por lo tanto, se cumple lo siguiente:
f ( x) f ( a ) f '(a) ( x a)
f '( x) f '(a) f ''(a) ( x a)
f ''( x) f ''(a) f '''(a) ( x a)
⋮
f n 1 ( x) f n 1 (a) f n (a)( x a) [3]

12. La Serie de Taylor (Cont.)
Utilizando lo obtenido en [3] y sustituyendo en la ecuación
[1], podemos desarrollar lo siguiente:
a h a h
f ( x) f ( a ) f '( x) dx f (a ) f '(a) f ''(a) ( x a) dx
a a
a h a h
f ( x) f ( a) f '(a) dx f ''(a) ( x a) dx
a a
a h a h
f ( x) f (a) f '(a) dx f ''(a) ( x a) dx
a a

13. La Serie de Taylor (Cont.)
a h a h a h
f ( x) f ( a) f '(a) dx f ''(a) x dx adx
a a a
h2
f ( x) f (a) f '(a) h f ''(a) [4]
2
Como se puede observar, la ecuación [4] nos muestra lo
que corresponde a la aproximación de segundo orden al
valor de f(x).

14. La Serie de Taylor (Cont.)
Si se repite este procedimiento n veces, suponiendo que
las derivadas de la función f(x) existen, se tendría la
aproximación n–1 al valor de la función:
h2 h3 ( n 1) h( n 1)
f ( x) f (a) f '(a) h f ''(a) f '''(a)  f (a ) Rn
2! 3! (n 1)!
En donde el residuo o el error que se comete al truncar la
serie infinita, para cualquier punto x es:
hn
Con: Rn n
f ( x) a x a h
(n)!

15. La Serie de Taylor (Cont.)
Finalmente, podemos concluir que la expansión de la Serie
de Taylor nos proporciona una aproximación al valor de
una función en un punto x en términos del valor de la
función y sus derivadas en un punto de referencia
conocido, denominado a.
Dicha expansión se realiza en una serie del tipo “Serie de
Potencias” en términos de la distancia h=x-a, entre el
punto x para el que se desea evaluar f(x) y el de
referencia a, donde se evalúan las derivadas.

16. La Serie de Taylor (Cont.)
En base a lo anterior, la forma más conocida de
representar a la Serie de Taylor es:
f i (a) i
f ( x) h
i 0 i!
O también:
f i (a)
f ( x) ( x a) i [5]
i 0 i!

17. Aproximación a f’(x)
Supongamos que se tiene una cierta función f(x), para la
cuál se desea obtener el valor de la primera derivada en
un cierto punto, que denotaremos como xi:
f’(xi)=?
f(x)
xi
La cuestión es: ¿Y si no recordamos como derivar?

18. Aproximación a f’(x)
Podemos recurrir a lo siguiente: Del cálculo diferencial e
integral, y de la geometría analítica, recordemos que el
valor de la derivada en un punto xi es exactamente igual al
valor de la pendiente de la tangente a la curva en dicho
punto. Es decir, en nuestro caso:
f’(xi)=m
f(x)
xi

19. Aproximación a f’(x)
Sería posible que, sin saber cálculo, aproximáramos el
valor de dicha derivada si escogemos un par de puntos a
ambos lados de xi, equidistantes por una distancia a la que
llamaremos h:
f’(xi)=m

m = aproximación a f’(xi)
f(x)
h h
xi

20. Aproximación a f’(x)
En la aproximación anterior tenemos un valor de error
muy significativo ya que h es grande. Si vamos acercando
ambos puntos hacia xi, es decir haciendo h0, el error
disminuye y nos aproximaremos al valor exacto:
f’(xi)=m

m = mejor aprox. a f’(xi)
f(x)
h0
xi

21. Aproximación a f’(x)
Como podemos notar, se tendrán que realizar una serie de
aproximaciones sucesivas para ir convergiendo hacia el
valor exacto de f’(xi).
Esto puede resultar en un proceso largo, tedioso y sobre
todo muy factible de errores al efectuar los cálculos.
Es aquí donde la Serie de Taylor resulta ser una
herramienta matemática muy valiosa, ya que nos
permitirá obtener una fórmula única para evaluar cualquier
primera derivada de cualquier función en un punto dado,
con tan sólo unos cálculos y sin existencia de iteraciones.

22. Aproximación a f’(x)
Veamos ahora la solución por Serie de Taylor.
Supongamos el mismo caso anterior, pero, ahora hacemos
una traslación de la f(x) de tal forma que el punto xi
coincida con el origen (x=0) y con una h de valor muy
pequeño (v.gr. 10-6):
f(x)
-h +h
xi=0
Por lo que los puntos adicionales quedarán en –h y +h.

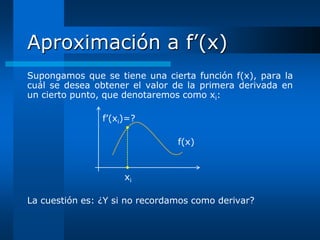
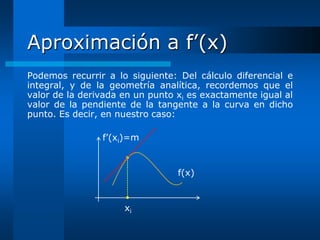
23. Aproximación a f’(x) (Cont.)
Tomemos la ecuación obtenida en [5] de la parte anterior
y desarrollemos la Serie de Taylor hasta sus tres primeros
términos, considerando al punto +h con respecto al punto
xi; es decir, como si xi fuese el punto a y +h el punto x.
Se tiene que: xi +h
(h 0)2
f ( h) f (0) f '(0)( h 0) f ''(0)
2!
h2 [a]
f ( h) f (0) f '(0) h f ''(0)
2

24. Aproximación a f’(x) (Cont.)
Hagamos lo mismo, pero ahora, considerando al punto -h
con respecto al punto xi; es decir, como si xi fuese el punto
a y -h el punto x.
Se tiene que: -h xi
( h 0)2
f ( h) f (0) f '(0)( h 0) f ''(0)
2!
h2
f ( h) f (0) f '(0) h f ''(0) [b]
2

25. Aproximación a f’(x) (Cont.)
Restando término a término las ecuaciones [a] y [b]
obtenemos lo siguiente:
h2
f ( h) f (0) f '(0) h f ''(0)
2
h2
f ( h) f (0) f '(0) h f ''(0)
2
f (h) f ( h) 2 f '(0) h
De aquí: f ( h) f ( h)
f '(0) [c]
2h

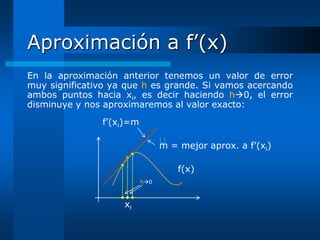
26. Aproximación a f’(x) (Cont.)
A manera de conclusión:
Si deseamos evaluar una derivada de una función f(x) en
cualquier punto x (y sin saber derivar !!!), bastará con
definir un cierto “Error permisible” ( ) muy pequeño (en el
rango de 10-5 a 10-8) y, basados en la fórmula obtenida en
[c], calcular:
f (x ) f (x )
f '( x)
2

27. Aproximación a f’’(x)
El proceso para la obtención de la segunda derivada en un
punto cualquiera x de cualquier función f(x) es muy similar
a lo estudiado anteriormente para la aplicación de la Serie
de Taylor para la primera derivada.
Vamos a utilizar las mismas ecuaciones [a] y [b] obtenidas
en el apartado anterior:
h2
f ( h) f (0) f '(0) h f ''(0) [a]
2
h2
f ( h) f (0) f '(0) h f ''(0) [b]
2

28. Aproximación a f’’(x) (Cont.)
Pero ahora vamos a sumar dichas ecuaciones [a] y [b]
término a término con lo que obtenemos:
h2
f ( h) f (0) f '(0) h f ''(0)
2
h2
f ( h) f (0) f '(0) h f ''(0)
2
f (h) f ( h) 2 f (0) f ''(0) h 2
De aquí: f ( h) 2 f (0) f ( h)
f ''(0) [d]
h2

29. Aproximación a f’’(x) (Cont.)
Finalmente:
Si deseamos evaluar la segunda derivada de una función
f(x) en cualquier punto x (y también, sin saber derivar
!!!), bastará con definir un cierto “Error permisible” ( )
muy pequeño (en el rango de 10-5 a 10-8) y, basados en la
fórmula obtenida en [d], calcular:
f (x ) 2 f ( x) f (x )
f ''( x) 2