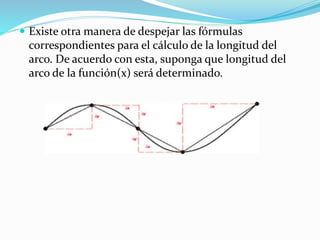
Este documento describe varios métodos para calcular la longitud de una curva. Explica que históricamente ha sido difícil determinar la longitud de segmentos irregulares, pero que el cálculo trajo fórmulas generales para algunos casos. Luego detalla que la longitud se puede aproximar sumando segmentos rectos pequeños o eligiendo puntos en la curva, y que para curvas suaves se puede usar el teorema de Pitágoras. Finalmente, presenta fórmulas para calcular la longitud cuando la curva está definida de forma paramétrica o polar.

2. Longitud De Curvas
 La longitud de arco de una curva, también llamada rectificación de una
curva, es la medida de la distancia o camino recorrido a lo largo de
una curva o dimensión lineal. Históricamente, ha sido difícil
determinar esta longitud en segmentos irregulares; aunque fueron
usados varios métodos para curvas específicas, la llegada
del calculo trajo consigo la fórmula general para obtener soluciones
cerradas para algunos casos.

3. La longitud de una curva plana
 se puede aproximar al sumar pequeños segmentos de recta que se
ajusten a la curva, esta aproximación será más ajustada entre más
segmentos sean y a la vez sean lo más pequeño posible. , escogiendo
una familia finita de puntos en C, y aproximar la longitud mediante la
longitud de la poligonal que pasa por dichos puntos. Cuantos más
puntos escojamos en C, mejor seria el valor obtenido como
aproximación de la longitud de C.

4.  Si la primera derivada de una función es continua en
[a,b] se dice que es suave y su gráfica es una curva
suave.
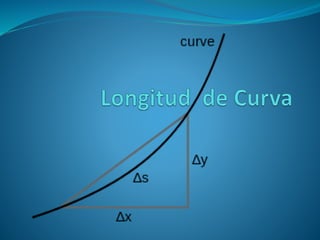
 Cuando la curva es suave, la longitud de cada pequeño
segmentos de recta se puede calcular mediante
el teorema de Pitágoras (dL)2=(dx)2+(dy)2.
 Si f es suave en [a,b], la longitud de la curva de f(x)
desde a hasta b es:

5.  Puede existir el caso, cuando la curva es definida en su
forma paramétrica, es decir, x = x (t) y y = y (t).
 El tercer caso es cuando la ecuación de la función se
describe en forma polar, esto es, r = f ( ), en ese caso, la
longitud del arco se puede encontrar por:

6.  Existe otra manera de despejar las fórmulas
correspondientes para el cálculo de la longitud del
arco. De acuerdo con esta, suponga que longitud del
arco de la función(x) será determinado.

7.  Para encontrar la longitud del arco (denotado como S)
en medio de los puntos b y a, una serie de triángulo
rectángulo se construye de manera que la hipotenusa
del triángulo cubra el arco correspondiente cuya
longitud será determinada. Para simplificar, la base del
triángulo se considera Δx tal que existe una y
correspondiente para cada Δx.
Ahora según el teorema de Pitágoras, obtenemos
Longitud de la Hipotenusa =

8.  La longitud total de todas las hipotenusas da el valor
aproximado de S. Esto es,
 Ahora, cuando el radicando es multiplicado por ,
obtenemos

9.  Por tanto, la S puede ser modificada
 Mientras menor sea el valor de Δx, más precisa será la
aproximación. Tenemos S, cuando el límite de Δx se
mueve hacia 0.Esto es,

10.  Vamos a considerar un ejemplo en el que la ecuación
de la curva se da como x = cos (a), y = sin(a), donde 0 ≤
a ≤ 2π.
 Diferenciando x e y, obtenemos
 dx / da = - sin (a) y dy / da = cos (a)
 Ahora, elevando al cuadrado y sumando ambos lados
 (dx / da)2 + (dy / da)2 = sin2 (a) + cos2 (a) = 1
 Por tanto, S = 1 da
 S = 2π.

11. Longitud de una curva plana
 Cuando queremos medir una curva, podemos dividir
en segmentos cortos y midiendo y sumando cada uno
de estos segmentos obtendríamos una longitud muy
aproximada de la curva. En la figura siguiente
tracemos una curva y luego tratar de conseguir una
expresión que nos permita medir con mayor exactitud
la longitud de una curva.

12. Ejercicio

13.  Hallar el volumen engendrado por las superficies
limitadas por las curvas y las rectas dadas al girar en
torno al eje OX:
y = sen x x = 0 x = π

14.  Hallar la longitud del arco de la curva 9 y2 = 4
x3 comprendido entre los puntos de la curva de
abscisa x = 0 y x = 3
Derivando,
de manera que

15.  Hallar la longitud del arco de curva y = ln(cos x)
comprendido entre los valores x = 0 y x = π/2
Empezamos calculando y' y su cuadrado:

17.  Hallar la longitud del arco de curva de la función
comprendido entre los valores x = - 1 y x = + 1
Recordamos que
de manera que f '(x) = sh(x), y resulta que