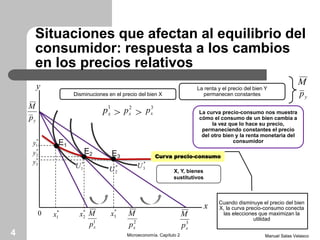
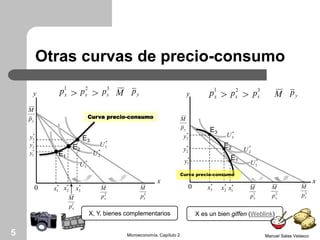
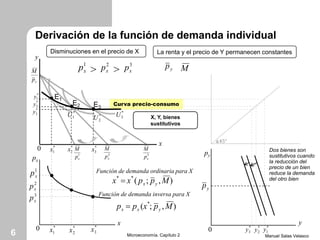
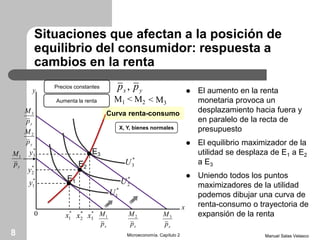
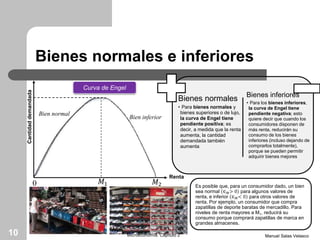
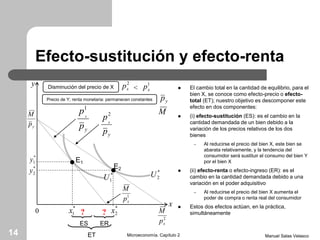
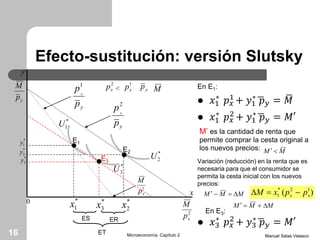
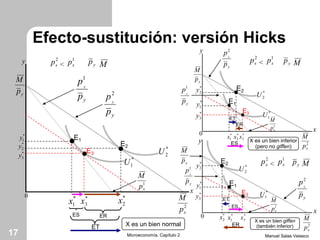
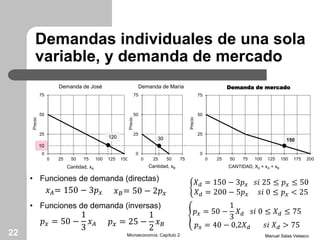
El capítulo 2 de microeconomía de Manuel Salas Velasco analiza cómo las elecciones de los consumidores cambian en respuesta a variaciones en precios y renta. Se exploran conceptos como la curva precio-consumo, la función de demanda y los efectos de sustitución y renta. Además, se discuten las funciones de demanda marshallianas y hicksianas, así como el comportamiento de bienes normales e inferiores.