Este documento presenta una serie de ejercicios de microeconomía relacionados con la teoría de la elección individual y del comportamiento de las empresas. En la primera sección, se analizan conceptos como la restricción presupuestaria, la función de demanda, la dualidad en el consumo y las elasticidades. La segunda sección aborda las funciones de producción Cobb-Douglas y Leontief. Finalmente, la tercera sección examina los bienes públicos, las externalidades y los impuestos y subsidios. El documento provee una introducción detallada a varios














































![La función de demanda Marshalliana de x2 se obtiene, de manera similar,
reemplazando (5) en la restricción:
Luego, para hallar las funciones de demanda Hiksiana, formulamos el problema dual:
mxp
p
xp
p 22
1
22
1
)4(
2
2
2
2
4
p
pm
x
mxppxp 22222 4
8
504.2
)4(2
)4(4520.2
x 2
313x2
Uxxas
xpxpMin
)4ln(ln:.
.
21
2211
)]4ln(ln[: 212211 xxUxpxp
634x
4
536,2
x
1
1](https://image.slidesharecdn.com/ifcastillopalominofce-161101152218/85/MICROECONOMIA-I-EJERCICIOS-RESUELTOS-47-320.jpg)



![c) Demostración de que U(x)≡v(P,m). Se sabe que U(x)= 12,21095. Entonces, se halla
v(P,m), para lo cual se remplazan las funciones de demanda Marshalliana en la
función de utilidad directa, y se reduce:
Finalmente:
Reemplazando los datos:
21
2
2
4
)4(
ln),(
pp
pm
mpv
)4)(2(4
)]4(4520.2[
ln),(
2
mpv
)978.200(ln),(
32
296.431.6
ln),(
mpv
mpv
....21095,12),( dqqlmpv
4
4)(
2
2
2
1
2
1
2
2
1
2
2
1
1
2
2
p
ep
X
pep
p
e
X
U
h
Uh
4
2
4
ln
2
4
ln),();(
2
2
1
2
21
p
pm
p
pm
mpvxxU
2
2
1
2
2
4
ln
2
4
ln),(
p
pm
p
pm
mpv](https://image.slidesharecdn.com/ifcastillopalominofce-161101152218/85/MICROECONOMIA-I-EJERCICIOS-RESUELTOS-51-320.jpg)

![c) Si consume 2Kg de pescado, x1= 2, entonces, de acuerdo a sus preferencias,
la ración de verduras (x2) que tendrá que consumir será:
x2= 4(2) = 8 Kg.
La utilidad que alcanza:
U = Mín. [2(2), ½(8)]
U = Mín. [4; 4]
O sea:
U = 4
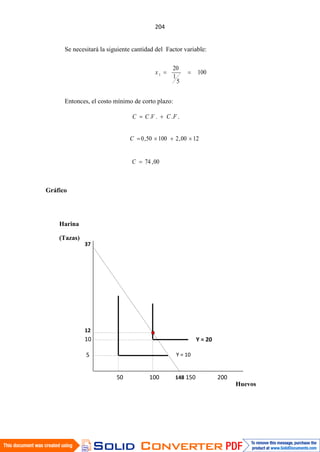
Gráfico:
x2 = 4x1
x2Ensalada
(Kg.)
X1
Pescado
(Kg.)](https://image.slidesharecdn.com/ifcastillopalominofce-161101152218/85/MICROECONOMIA-I-EJERCICIOS-RESUELTOS-53-320.jpg)















![c) Cuando p1 cae a 1, el instrumental analítico convencional para hallar el equilibrio muestra
una incongruencia, veamos porque:
Las demandas serían:
Luego, éstas se reemplazarían en la función de utilidad, obteniéndose:
U = Mín. [857.1; 857.1]
Entonces, U = 857
El sistema de ecuaciones que contendrá a esta U será:
Pero veamos que sucede en el gráfico:se observa que el supuesto equilibrio viola el
principio de tangencia, pues la recta presupuestaria cruza el conjunto de
consumo interior. Entonces, el consumidor puede alcanzar un mayor nivel de
utilidad. Así, la curva de indiferencia puede desplazarse hasta lograr la tangencia
con la recta de balance.Esto ocurrirá en el punto X*(1.200; 0), configurándose
una solución esquina
X*(1.200; 0)
X (171; 343)
857
600
428,5
400
342,9
U = 857
U *
= 1200
x2
x1
9.342
)3(21
)1200(2
4.171
)3(21
1200
21 xx
857x2x
857xx3
21
21](https://image.slidesharecdn.com/ifcastillopalominofce-161101152218/85/MICROECONOMIA-I-EJERCICIOS-RESUELTOS-69-320.jpg)















































































![Luego, la función de costos:
b) Gráfica del CMe y CMg
A[(1-α)w1]1-α
Y (αw2)1-α
C= W1
Y[(1-α)w1]α
W2
A(αW2)α
A
Yww
YwC
1
21
1
),(
1
1
),(
11
21
A
wYw
YwC
Y
C
CMg
y
Y
C
CMe
)1(
)1()1(1
21
)1(
)1()1(
),(
A
wYw
YwC
)1(
1
21
)1(
)1(
),(
A
wYw
YwC
)1(
1
21
)1(
1
),(
A
wYw
YwC](https://image.slidesharecdn.com/ifcastillopalominofce-161101152218/85/MICROECONOMIA-I-EJERCICIOS-RESUELTOS-149-320.jpg)






()(1
2
)(1
1
)()(1
)(
1
)()(1
)](1[
1
)()(1
1
wwww
wwww
))]((1[
2
))]((1[
1
)(1
1
21
)(1
2
)(1
1
)(1
)(
)()(
),( ww
K
P
wwKww
K
P
PwP
)(1
2
)(1
1
)(1
1
)(1
2
)(1
1
)(1
)(
)()(
),( ww
K
P
Kww
K
P
PwP
)(1
2
)(1
1
(1
1
)(1
)(
)(1
1
)(1
2
)(1
1
(1
1
)(1
)(
)(1
)(
)()(),( wwPKwwPKwP
)(1
2
)(1
1
)(1
1
)(1
)(
)(1
1
)(1
)(
)()(),( wwPKwP
)(1
2
)(1
1
)(1
1
),( wwPMwP](https://image.slidesharecdn.com/ifcastillopalominofce-161101152218/85/MICROECONOMIA-I-EJERCICIOS-RESUELTOS-156-320.jpg)






![Reemplazando (4) y (5) en (I), y simplificando :
4. Dada la siguiente función de producción:
f(x1,x2) = 4(x1
0,75
+ x2
0,75
)
a) Obtenga las demandas no condicionales y la función de oferta.
b) Determine la función de beneficios.
c) Compruebe el Teorema de Hotelling.
d) Obtenga la función de costos.
e) Compruebe el Lema de Sheppard
Solución
a) Las Demandas no condicionales (DNC) y la Función de oferta
Partimos de la ecuación de beneficios, realizando los reemplazos respectivos:
π = P.Y - C
π = P.[4(x1
0,75
+ x2
0,75
)] - w1x1- w2x2 .........(α)
Luego, aplicando derivadas parciales, y despejando, obtenemos las DNC:
dπ/dx1= 3Px1
–0,25
- w1= 0
21
21
)1(
)1(
ww
ww
4
1
1
3
),(
w
P
wPx
P
w
x
3
125,0
1](https://image.slidesharecdn.com/ifcastillopalominofce-161101152218/85/MICROECONOMIA-I-EJERCICIOS-RESUELTOS-163-320.jpg)




,(
ww
wwY
YwC
3/43
2
3
1
2
4
1
3/44
21
3/4
)](4[
),(
ww
wwYwwY
YwC
3/43
2
3
1
3
2
3
121
3/4
)](4[
)(
),(
ww
wwwwY
YwC
i
i
w
YwC
Ywx
),(
),(
)(768)](256)[3/1()](256[
),(
21
3
4
2
1
3/43
2
3
1
3/13
2
3
12
3
4
1
1
1
wwYwwwwwwYx
w
C
Ywx](https://image.slidesharecdn.com/ifcastillopalominofce-161101152218/85/MICROECONOMIA-I-EJERCICIOS-RESUELTOS-168-320.jpg)
](256[)](256[ 3
2
3
1
3
13/13
2
3
12
3
4
3/13
2
3
12
3
4
1
ww
w
wwwYwwwYx
]
)(
1[)](256[ 3
2
3
1
3
13/13
2
3
12
3
4
1
ww
w
wwwYx
)(
)()256( 3
2
3
1
3
23/13
2
3
1
3/1
2
3
4
1
ww
w
wwwYx
3/4
3
2
3
1
3
2
1
)](4[
),(
ww
wY
Ywx
3/43
2
3
1
3/44
2
3
4
1 )()4( wwwYx
)(768)](256)[3/1()](256[
),(
21
3
4
2
2
3/43
2
3
1
3/13
2
3
11
3
4
2
2
wwYwwwwwwY
w
C
Ywx
]
)(
[)](256[ 3
2
3
1
3
1
3
2
3
13/13
2
3
12
3
4
1
ww
www
wwwYx
3/43
2
3
1
3/144
2
3
4
1 )]()4( wwwYx
3/43
2
3
1
4
2
3
4
1
)](4[ ww
wY
x](https://image.slidesharecdn.com/ifcastillopalominofce-161101152218/85/MICROECONOMIA-I-EJERCICIOS-RESUELTOS-169-320.jpg)
](256[)](256[ 3
2
3
1
3
23/13
2
3
11
3
4
3/13
2
3
11
3
4
2
ww
w
wwwYwwwYx
]
)(
1[)](256[ 3
2
3
1
3
23/13
2
3
11
3
4
2
ww
w
wwwYx
)(
)()256( 3
2
3
1
3
13/13
2
3
1
3/1
1
3
4
2
ww
w
wwwYx
3/43
2
3
1
3/44
1
3
4
2 )()4( wwwYx
]
)(
[)](256[ 3
2
3
1
3
2
3
2
3
13/13
2
3
12
3
4
2
ww
www
wwwYx
3/4
3
2
3
1
3
1
2
)](4[
),(
ww
wY
Ywx
3/43
2
3
1
4
1
3
4
2
)](4[ ww
wY
x](https://image.slidesharecdn.com/ifcastillopalominofce-161101152218/85/MICROECONOMIA-I-EJERCICIOS-RESUELTOS-170-320.jpg)
![Solución
a) Las Demandas no condicionales y la función de oferta
Partimos de la ecuación de beneficios:
π = P.Y - C
Reemplazamos en ésta, la función de producción
π = P.[ 3(x1
1/3
+ x2
1/3
+ x3
1/3
)] - w1x1- w2x2 - w3x3........(a)
Aplicamos la condición de primer orden:
dπ/dx1= Px1
–2/3
- w1= 0 ........ (1)
dπ/dx2= Px2
–2/3
- w2 = 0 ....... (2)
dπ/dx3= Px3
–2/3
- w3 = 0 ....... (3)
de (1) :
de (2) :
de (3) :
2/3
1
1 ),(
w
P
wPx
P
w
x 13/2
1
2/3
2
2 ),(
w
P
wPx
P
w
x 23/2
2
2/3
3
3 ),(
w
P
wPx
P
w
x 33/2
3](https://image.slidesharecdn.com/ifcastillopalominofce-161101152218/85/MICROECONOMIA-I-EJERCICIOS-RESUELTOS-171-320.jpg)






















![9. Si una empresa tiene la siguiente función de producción:
Y = [4X2(X1+2)]
1/3
y los costos de los factores son w1= w2 =1
a) Halle la curva de oferta de largo plazo
b) Si el factor X2 se mantiene fijo en X2 = 10 derive la curva de oferta a corto plazo
Solución
Se plantea el problema dual:
Min. w1x1 + w2 x2
C.P.O.:
Resolviendo el sistema, se divide (1)/(2), y se simplifica, obteniéndose la relación
entre x1 y x2:
2
1
1
3
2
12
2
3
2
12
)84()2(4
3
1
)4()2(4
3
1
w
w
xxx
xxx
Yxxas 3
1
12 )2(4:..
3
1
122211 )2(4 xxYxwxw
)1(......0)4()2(4
3
1
2
3
2
121
1
xxxw
x
)2(.....0)84()2(4
3
1
1
3
2
122
2
xxxw
x
)3(......0)2(4 3
1
12 xxY
2
1
1
2
)2( w
w
x
x](https://image.slidesharecdn.com/ifcastillopalominofce-161101152218/85/MICROECONOMIA-I-EJERCICIOS-RESUELTOS-194-320.jpg)















![x1= y x2 = y x3 = y x4 = y
El costo de producción de cada proceso:
C(w1, w2, y) = w1 y + w2 y C(w3, w4, y) = w3 y + w4 y
Reemplazando los datos:
C(w1, w2, y) = (1)(1) + (2)(1) C(w3, w4, y) = (3)(1) + (4)(1)
= 3 = 7
Por tanto, se prefiere el proceso menos costoso -el proceso que emplea los factores
x1 y x2- y se descarta el más costoso. Así, la demanda de factores se representa por el
vector
X(x1, x2, x3, x4) ≡ X(1, 1, 0, 0)
b) La función de costos se obtiene, agregando las funciones de costos de ambos
procesos:
C(w1, w2, y) = (w1 + w2)y C(w3, w4, y) = (w3 + w4)y
Entonces:
C(w1, w2, w3, w4, y) = Mín. [w1 + w2; w3 + w4] y
c) Si variamos los insumos en t > 0, entonces la función de producción:
4321
4321
4321
,.,.'
,.,.'
,.,.'
xxMínxxMínty
xxtMínxxtMíny
txtxMíntxtxMíny](https://image.slidesharecdn.com/ifcastillopalominofce-161101152218/85/MICROECONOMIA-I-EJERCICIOS-RESUELTOS-211-320.jpg)








![Nivel de ganancias de equilibrio:
π = P.Y – C
= P.Y – (w1 x1 + w2 x2)
= (3,5)(625) –[25(25) + 30(125)]
= 2.187,5 – 4.375
π = - 2.187.5
Nivel de ganancias gastando 10,500 Y = 3.600
π = P.Y – C
= P.Y – (w1 x1 + w2 x2)
= (3,5)(3.600) –[25(60) + 30(300)]
= 12.600 –10.500
π = 2.100
En este caso, cuando se tiene rendimientos crecientes a escala el equilibrio va
implicar pérdidas (CMe> P=Cmg) por ello cuanto más se produzca las pérdidas se
reducirán, incluso habrán beneficios extraordinarios.
2
1
*
2 5 Yx
2
1
*
1 )500.2(x
25*
1x
2
1
*
2 )625(5x
125
*
2x](https://image.slidesharecdn.com/ifcastillopalominofce-161101152218/85/MICROECONOMIA-I-EJERCICIOS-RESUELTOS-220-320.jpg)




















































![273
Las loterías o las opciones de una lotería están sujetas a las preferencias del
consumidor, así:
P ° x + (1- p) ° y q ° w + (1- q) ° z
óP ° x (1- p) ° y
Por lo tanto, se les puede asignar una función de utilidad que describa tales preferencias,
entonces:
U(P ° x + (1- p) ° y) > U(q ° w + (1- q) ° z)
ó U(P ° x ) > U( (1- p) ° y )
Valor Esperado
También denominado Esperanza de pagos o Equivalente cierto, mide el rendimiento
medio de la lotería ponderando sus posibles resultados o pagos por su respectiva
probabilidad.
VE = p . x + (1- p) .y
Función de utilidad esperada
La función de utilidad esperada indica la valoración o utilidad de la lotería o juego para
el consumidor. Se obtiene ponderando las utilidades de los posibles resultados por su
probabilidad respectiva.
FUE = p .U(x) + (1- p) .U(y)
Función de utilidad del valor esperado
La función de utilidad del valor esperado indica la utilidad del valor esperado o
equivalente cierto, es decir, representa la utilidad que obtendría el consumidor si tuviese
a su alcance el valor esperado.
FUVE = U[p . x + (1- p) . y ]](https://image.slidesharecdn.com/ifcastillopalominofce-161101152218/85/MICROECONOMIA-I-EJERCICIOS-RESUELTOS-273-320.jpg)



