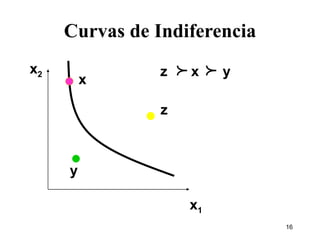
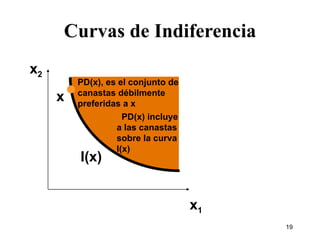
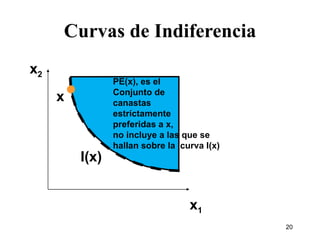
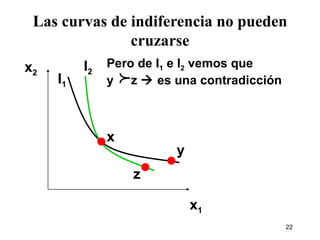
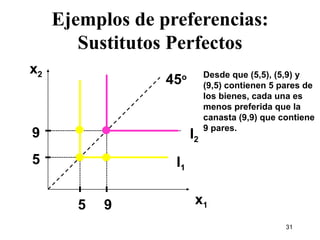
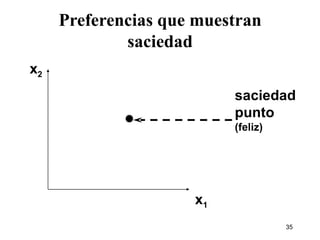
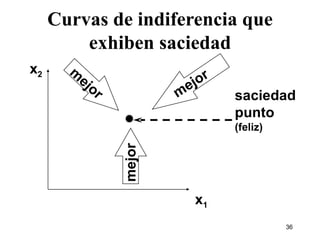
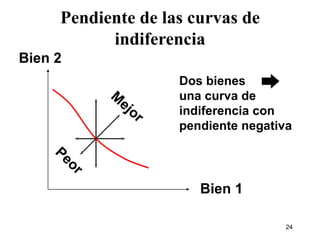
1) El documento describe los conceptos básicos de las preferencias del consumidor, incluyendo canastas de consumo, relaciones de preferencia, curvas de indiferencia y relación marginal de sustitución. 2) Explica que las preferencias del consumidor pueden ser completas, reflexivas y transitivas y cómo esto afecta las curvas de indiferencia. 3) Resalta que la pendiente de las curvas de indiferencia mide la relación marginal de sustitución entre bienes.

1. Módulo 3 Las Preferencias

2. Racionalidad en Economía El consumidor siempre escoge la alternativa más preferida de su conjunto de alternativas factibles En consecuencia debemos elaborar el modelo para las preferencias del consumidor

3. Cestas o Canastas de Consumo Consisten en una lista completa de los bienes y los servicios a que se refiera el problema de elección que se está investigando

4. Las preferencias del consumidor Comparando dos canastas diferentes de consumo, x e y: Preferencia estricta: x es preferida a y Preferencia débil: x es al menos tan preferida como y Indiferencia: x es igualmente preferida que y

5. Preferencia estricta, preferencia débil e indiferencia son todas las relaciones de preferencia Específicamente, éstas son preferencias ordinales; es decir, ellas sólo determinan el orden en que las canastas son preferidas Las preferencias del consumidor

6. denota preferencia estricta; x y singinifica que la canasta x es estríctamente preferida a la canasta y y Las preferencias del consumidor  

7. denota preferencia estricta; x y significa que la canasta x es estríctamente preferida a la canasta y  denota indiferencia; x  y significa que x e y son igualmente preferidas Las preferencias del consumidor  

8. denota preferencia estrícta x y significa que la canasta x es estríctamente preferida a la canasta y  denota indiferencia; x  y significa que x e y son igualmente preferidas denota preferencia débil; x y significa que x es preferida al menos tanto como y Las preferencias del consumidor   ~  ~ 

9. x y e y x implican que x  y. Las preferencias del consumidor ~  ~ 

10. x y y, y no x implica x y. Las preferencias del consumidor  ~  ~ 

11. Supuestos acerca de las preferencias Completas: Para cualquier par de canastas x e y siempre es posible determinar que x y ó y x ~  ~ 

12. Reflexivas: Para cualquier canasta x, la canasta x es siempre al menos tan preferida como ella misma x x. Supuestos acerca de las preferencias ~ 

13. Transitivas: Si x es al menos tan preferida como y, y y es al menos tan preferida como z, entonces x es al menos tan preferida como z x y y y z x z. Supuestos acerca de las preferencias ~  ~  ~ 

14. Curvas de Indiferencia Tomemos como referencia la canasta x’. El conjunto de todas las canastas igualmente preferidas a x’ es la curva de indiferencia que contiene a x’; el conjunto de todas las canastas donde y  x’. En la medida que una “curva” de indiferencia no siempre es una curva un mejor nombre sería el “conjunto” indiferencia.

15. Curvas de Indiferencia x 2 x 1 x” x”’ x’  x”  x”’ x’

16. Curvas de Indiferencia x 2 x 1 z x y   x y z

17. Curvas de Indiferencia x 2 x 1 x Todas las canastas en I 1 son estríctamente preferidas a todas las canastas en I 2 y z Todas las canastas en I 2 son estríctamente preferidas a todas las canastas en I 3 I 1 I 2 I 3

18. Curvas de Indiferencia x 2 x 1 I(x’) x I(x) PD(x), es el conjunto de canastas débilmente preferidas a x PD = Preferencia débil

19. Curvas de Indiferencia x 2 x 1 PD(x), es el conjunto de canastas débilmente preferidas a x PD(x) incluye a las canastas sobre la curva I(x) x I(x)

20. Curvas de Indiferencia x 2 x 1 PE(x), es el Conjunto de canastas estríctamente preferidas a x, no incluye a las que se hallan sobre la curva I(x) x I(x)

21. Las curvas de indiferencia no pueden cruzarse x 2 x 1 x y z I 1 I 2 De I 1 , x  y. De I 2 , x  z En consecuencia y  z

22. Las curvas de indiferencia no pueden cruzarse x 2 x 1 x y z I 1 I 2 Pero de I 1 e I 2 vemos que y z  es una contradicción 

23. Pendiente de las curvas de indiferencia Cuando más de un bien siempre es preferido, entonces se trata de un bien Si todos los bienes son bienes, entonces las curvas de indiferencia tienen pendiente negativa

24. Pendiente de las curvas de indiferencia Mejor Peor Bien 2 Bien 1 Dos bienes una curva de indiferencia con pendiente negativa

25. Si menos de un bien siempre es preferido, entonces el bien es un mal Pendiente de las curvas de indiferencia

26. Pendiente de las curvas de indiferencia Mejor Peor Bien 2 Mal 1 Un bien y un mal curva de indiferencia con pendiente positiva.

27. Ejemplos de preferencias: Sustitutos Perfectos Si un consumidor siempre considera que unidades del bien 1 y 2 son equivalentes, entonces los bienes son sustitutos perfectos y sólo la cantidad total de los dos bienes determina el orden de sus preferencias

28. x 2 x 1 8 8 15 15 Las pendientes son constantes e iguales a - 1 I 2 I 1 Todas las canastas en la CI I 2 tienen un total de 15 unidades y son estríctamente preferidas A todas las canastas en la CI I 1 , que tienen sólo 8 unidades en ella Ejemplos de preferencias: Sustitutos Perfectos

29. Si un consumidor siempre consume los bienes 1 y 2 en una cierta proporción fija (por ejemplo, uno a uno), entonces los bienes son complementos perfectos y sólo el número de pares de unidades de los dos bienes determina el orden de preferencias de las canastas Ejemplos de preferencias: complementos perfectos

30. Ejemplos de preferencias: Sustitutos Perfectos x 2 x 1 I 1 45 o 5 9 5 9 Las canastas (5,5), (5,9) y (9,5) contienen 5 pares de cada uno de los bienes y son igualmente preferidas

31. Ejemplos de preferencias: Sustitutos Perfectos x 2 x 1 I 2 I 1 45 o 5 9 5 9 Desde que (5,5), (5,9) y (9,5) contienen 5 pares de los bienes, cada una es menos preferida que la canasta (9,9) que contiene 9 pares.

32. Ejemplo de preferencias: Males x 2 I 2 I 1 I 3 I 4 x 1

33. Ejemplo de preferencias: Neutrales x 2 I 2 I 1 I 3 x 1

34. Preferencias que muestran saciedad Una canasta estríctamente preferida a cualquier otra es un punto de saciedad o un punto feliz ¿Cómo se presentan las curvas de indiferencia cuando se tienen preferencias que muestran saciedad?

35. Preferencias que muestran saciedad x 2 x 1 saciedad punto (feliz)

36. Curvas de indiferencia que exhiben saciedad x 2 x 1 mejor mejor mejor saciedad punto (feliz)

37. Curvas de indiferencia que exhiben saciedad x 2 x 1 mejor mejor mejor saciedad punto (feliz)

38. Curvas de indiferencia para bienes discretos Un bien es infinitamente divisible si puede ser adquirido en cualquier cantidad; por ejemplo, el agua o el queso Un bien es discreto si viene en unidades fijas de 1, 2, 3, … etc.; por ejemplo aviones, barcos, refrigeradoras

39. Supongamos que el bien 2 es un bien infinitamente divisible (gasolina) mientras el bien 1 es un bien discreto (avión). ¿Cómo se presentará la curva de indiferencia? Curvas de indiferencia para bienes discretos

40. Curvas de indiferencia para bienes discretos Gasolina avión 0 1 2 3 4 Las curvas de indiferencia son conjuntos de puntos discretos

41. Preferencias regulares Una preferencia es una preferencia “regular” si es monotónica y convexa Monotonicidad: más de cualquier bien siempre es preferido (en otras palabras, no saciedad y todos los bienes son bienes)

42. Convexidad: una combinación de canastas es (al menos débilmente) preferida que las canastas iniciales. Por ejemplo, la combinación 50, 50 de las canastas x e y es z = (0.5)x + (0.5)y donde z es al menos tan preferida como x o y Convexidad

43. x 2 y 2 x 2 +y 2 2 x 1 y 1 x 1 +y 1 2 x y z = x+y 2 Es estríctamente preferida frenta a x e y Convexidad

44. x 2 y 2 x 1 y 1 x y z =(tx 1 +(1-t)y 1 , tx 2 +(1-t)y 2 ) es preferida a x e y para todo 0 < t < 1. Convexidad

45. x 2 y 2 x 1 y 1 x y Las preferencias son estríctamente convexas cuando todas las combinaciones z son estríctamente preferidas a sus componentes. z Convexidad

46. Convexidad La combinación ( x 1 + x 2 )/2, ( y 1 + y 2 )/2 será preferida a ( x 1 , y 1 ) o ( x 2 , y 2 ) x y U 1 x 2 y 1 y 2 x 1 (x 1 + x 2 )/2 Esto implica que combinaciones “bien balanceadas” se prefieren a combinaciones en las que predominan un bien (y 1 + y 2 )/2

47. Preferencias regulares con convexidad débil x’ y’ z’ Las preferencias son débilmente convexas si al menos una combinación z es igualmente preferida a la combinación x e y x z y

48. Preferencias no convexas x 2 y 2 x 1 y 1 z mejor La combinación z es menos preferida que x o y x y

49. Otras preferencias no convexas x 2 y 2 x 1 y 1 z mejor La combinación z es menos preferida que x o y

50. Pendiente de las curvas de indiferencia La pendiente de una curva de indiferencia es su Relación Marginal de Sustitución (RMS) ¿Cómo se puede estimar la RMS?

51. Relación Marginal de Sustitución x 2 x 1 x’ La RMS en x’ es la pendiente de la curva de indiferencia en x’

52. Relación Marginal de Sustitución x 2 x 1 La RMS en x’ es lim {  x 2 /  x 1 }  x 1 0 = dx 2 /dx 1 en x’  x 2  x 1 x’

53. Relación Marginal de Sustitución La pendiente negativa de la curva de indiferencia mide la RMS - la tasa a la cual un individuo negociaría la cantidad de un bien y por una unidad adicional del bien x La RMS disminuye a medida que x se sustituye por y - los individuos prefieren un balance en sus elecciones de consumo

54. Relación Marginal de Sustitución x 2 x 1 dx 2 dx 1 dx 2 = RMS  dx 1 , en consecuencia, en x’, la RMS es la tasa a la cual el consumidor está dispuesto a cambiar el bien 2 por una pequeña cantidad del bien 1. x’

55. RMS y propiedades de la curva de indiferencia mejor peor Bien 2 Bien 1 Dos bienes curva indiferencia de pendiente negativa RMS < 0

56. RMS y propiedades de la curva de indiferencia Mejor Peor Bien 2 Mal 1 Un bien y un mal pendiente positiva de la curva de indiferencia RMS > 0.

57. RMS y propiedades de la curva de indiferencia Bien 2 Bien 1 RMS = - 5 RMS = - 0.5 La RMS siempre se incrementa con x 1 (se hace menos negativa) si y sólo si las preferencias son estríctamente convexas. En valor absoluto, la TMgS es siempre decreciente

58. RMS y propiedades de la curva de indiferencia x 1 x 2 RMS = - 0.5 RMS = - 5 La RMS disminuye (se hace más negativa) cuando x 1 se incrementa en preferencias no convexas. La RMS se incrementa en valor absoluto

59. RMS y propiedades de la curva de indiferencia x 2 x 1 RMS = - 0.5 RMS = - 1 RMS = - 2 La RMS no siempre se incrementa cuando x 1 se incrementa en preferencias no convexas. La RMS no siempre disminuye en valor absoluto