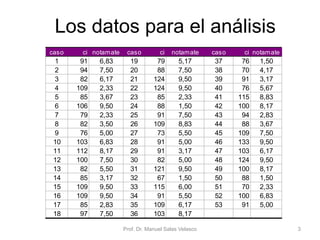
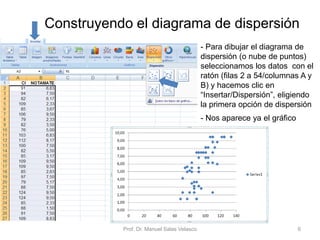
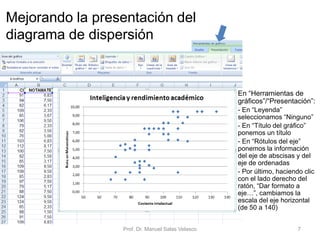
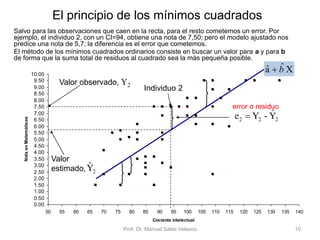
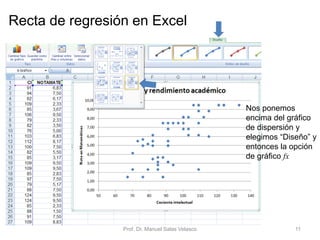
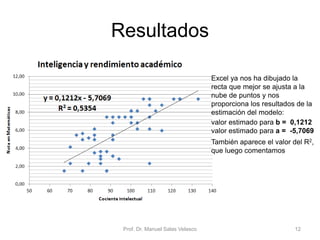
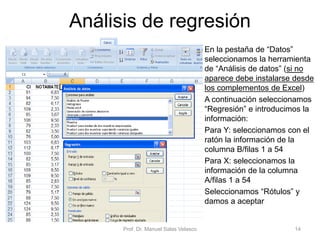
El documento presenta un análisis de regresión utilizando datos del rendimiento académico de estudiantes de primaria en relación con su cociente intelectual. Se busca determinar si un mayor CI se asocia a mejores notas en matemáticas, utilizando Excel para graficar y ajustar una recta de regresión mínima cuadrática. Se concluye que el CI explica un 53,5% de la variación en las notas, permitiendo hacer predicciones sobre el rendimiento escolar.

1. Tutoriales Prácticos de Economía
Prof. Dr. Manuel Salas Velasco
ANÁLISIS DE REGRESIÓN
USANDO LA HOJA DE CÁLCULO
EXCEL
1

2. ¿Qué factores afectan al
rendimiento académico?
• La tabla adjunta en la siguiente diapositiva contiene
datos reales de un colegio concertado de Granada
correspondientes al cuarto curso de primaria del año
escolar 2000-2001. Tenemos 53 casos (niños/as) e
información sobre dos variables para cada caso. La
definición de las variables es como sigue:
• CI: cociente intelectual.
• NOTAMATE: nota media en Matemáticas (3ª evaluación).
Media de los tres apartados: a) identificar, plantear y
resolver problemas; b) conocer los conceptos
matemáticos básicos; y c) dominar cuatro operaciones
básicas con números naturales y decimales.
2Prof. Dr. Manuel Salas Velasco

3. Los datos para el análisis
caso ci notamate caso ci notamate caso ci notamate
1 91 6,83 19 79 5,17 37 76 1,50
2 94 7,50 20 88 7,50 38 70 4,17
3 82 6,17 21 124 9,50 39 91 3,17
4 109 2,33 22 124 9,50 40 76 5,67
5 85 3,67 23 85 2,33 41 115 8,83
6 106 9,50 24 88 1,50 42 100 8,17
7 79 2,33 25 91 7,50 43 94 2,83
8 82 3,50 26 109 8,83 44 88 3,67
9 76 5,00 27 73 5,50 45 109 7,50
10 103 6,83 28 91 5,00 46 133 9,50
11 112 8,17 29 91 3,17 47 103 6,17
12 100 7,50 30 82 5,00 48 124 9,50
13 82 5,50 31 121 9,50 49 100 8,17
14 85 3,17 32 67 1,50 50 88 1,50
15 109 9,50 33 115 6,00 51 70 2,33
16 109 9,50 34 91 5,50 52 100 6,83
17 85 2,83 35 109 6,17 53 91 5,00
18 97 7,50 36 103 8,17
3Prof. Dr. Manuel Salas Velasco

4. Nuestro objetivo
• Estamos interesados en saber si el cociente
intelectual influye en el rendimiento escolar (la
nota obtenida en Matemáticas)
• Nuestra hipótesis de partida que queremos
contrastar es que un mayor cociente intelectual
se asocia con un mayor rendimiento
académico
• El primer paso sería inspeccionar visualmente la
información para ver si esto se cumple
• Para ello introducimos en Excel la información de la
tabla y dibujamos un diagrama de dispersión
4Prof. Dr. Manuel Salas Velasco

5. Introduciendo la información en Excel
Prof. Dr. Manuel Salas Velasco 5
• En la primera fila ponemos los nombres de
las variables, y a partir de la segunda fila
introducimos la información numérica
(llegaría hasta la fila 54)
• Para que sea más fácil la construcción de
gráficos, en la primera columna
introducimos la información de la variable
independiente (CI) y en la segunda
columna la correspondiente a la
dependiente (NOTAMATE)
• Tarea: ¡introduzca usted los datos!

6. Prof. Dr. Manuel Salas Velasco 6
Construyendo el diagrama de dispersión
- Para dibujar el diagrama de
dispersión (o nube de puntos)
seleccionamos los datos con el
ratón (filas 2 a 54/columnas A y
B) y hacemos clic en
“Insertar/Dispersión”, eligiendo
la primera opción de dispersión
- Nos aparece ya el gráfico

7. Prof. Dr. Manuel Salas Velasco 7
En “Herramientas de
gráficos”/“Presentación”:
- En “Leyenda”
seleccionamos “Ninguno”
- En “Título del gráfico”
ponemos un título
- En “Rótulos del eje”
ponemos la información
del eje de abscisas y del
eje de ordenadas
- Por último, haciendo clic
con el lado derecho del
ratón, “Dar formato a
eje…”, cambiamos la
escala del eje horizontal
(de 50 a 140)
Mejorando la presentación del
diagrama de dispersión

8. Análisis econométrico
• A partir de la observación de los puntos, se observa una tendencia general a que los
alumnos con más inteligencia (X) obtienen una mejor nota en Matemáticas (Y); a
este tipo de relación se le conoce como correlación directa o positiva
• Si Y tiende a incrementarse cuando se incrementa X, entonces tendríamos: Y = f (X)
• Pero la inspección visual del diagrama de dispersión también sugiere que la relación
entre las dos variables es esencialmente lineal:
– Por tanto, si la relación f que liga Y con X es lineal, tendríamos la ecuación de una recta:
Y = a + b X
– Mediante la letra a designamos la ordenada en el origen (término constante), y
mediante la letra b la pendiente de la recta; la pendiente b es el cambio de Y
(rendimiento escolar) asociado con un cambio unitario en X (inteligencia)
• Sin embargo, en la práctica, la relación determinística anterior es inadecuada porque
hay otros factores que influyen en Y; un modelo empírico necesariamente debe
incorporar este hecho de la siguiente forma:
Y = a + b X + error
– El término de error, e, es una variable aleatoria que se añade para reflejar, entre otros
aspectos, factores que también explican el rendimiento pero que no los hemos tenido en
cuenta en el análisis
– La expresión anterior, en donde solo figura una única variable explicativa (el cociente
intelectual), se le conoce como modelo de regresión lineal simple
Prof. Dr. Manuel Salas Velasco 8

9. Ajustando una recta a los datos
• Nuestro objetivo es ahora ajustar una recta a la nube de
puntos, buscando tanto la ordenada en el origen a como
la pendiente b (los parámetros del modelo)
• Ahora bien, en la práctica podrían ajustarse infinidad de
rectas; ¿cuál es la mejor?
• El programa Excel nos va a buscar la mejor recta,
llamada recta de regresión mínimo-cuadrática
• El gorro encima de a y b indican valores concretos que
toman los parámetros una vez estimados
Prof. Dr. Manuel Salas Velasco 9
Xˆaˆ b

10. El principio de los mínimos cuadrados
0.00
0.50
1.00
1.50
2.00
2.50
3.00
3.50
4.00
4.50
5.00
5.50
6.00
6.50
7.00
7.50
8.00
8.50
9.00
9.50
10.00
50 55 60 65 70 75 80 85 90 95 100 105 110 115 120 125 130 135 140
Cociente intelectual
NotaenMatemáticas
Individuo 2
Valor observado, Y2
Valor
estimado,
error o residuo
2Yˆ
222 Y-Ye ˆ
10Prof. Dr. Manuel Salas Velasco
Xˆaˆ b
Salvo para las observaciones que caen en la recta, para el resto cometemos un error. Por
ejemplo, el individuo 2, con un CI=94, obtiene una nota de 7,50; pero el modelo ajustado nos
predice una nota de 5,7; la diferencia es el error que cometemos.
El método de los mínimos cuadrados ordinarios consiste en buscar un valor para a y para b
de forma que la suma total de residuos al cuadrado sea la más pequeña posible.

11. Recta de regresión en Excel
Prof. Dr. Manuel Salas Velasco 11
Nos ponemos
encima del gráfico
de dispersión y
elegimos “Diseño” y
entonces la opción
de gráfico fx

12. Resultados
Prof. Dr. Manuel Salas Velasco 12
Excel ya nos ha dibujado la
recta que mejor se ajusta a la
nube de puntos y nos
proporciona los resultados de la
estimación del modelo:
valor estimado para b = 0,1212
valor estimado para a = -5,7069
También aparece el valor del R2,
que luego comentamos

13. Test de hipótesis
• Ahora bien, no basta con haber obtenido los
valores para la ordenada en el origen y la
pendiente de la recta
• Es importante contrastar la hipótesis de
partida “a mayor inteligencia, mayor nota en
Matemáticas”
• Para ello debemos comprobar que el
coeficiente estimado b, la pendiente, es
estadísticamente significativo
• ¿Cómo lo hacemos en Excel?
Prof. Dr. Manuel Salas Velasco 13

14. Análisis de regresión
• En la pestaña de “Datos”
seleccionamos la herramienta
de “Análisis de datos” (si no
aparece debe instalarse desde
los complementos de Excel)
• A continuación seleccionamos
“Regresión” e introducimos la
información:
• Para Y: seleccionamos con el
ratón la información de la
columna B/filas 1 a 54
• Para X: seleccionamos la
información de la columna
A/filas 1 a 54
• Seleccionamos “Rótulos” y
damos a aceptar
Prof. Dr. Manuel Salas Velasco 14

15. Resultados de la regresión
Resaltamos en amarillo los resultados de la regresión que nos interesan
Notas: 1. Se ha seleccionado el formato de número con cuatro
decimales
2. Excel, a la ordenada en el origen, le llama intercepción
De nuevo, la recta de regresión sería:
NOTAMATE = -5,707 + 0,121 CI
Prof. Dr. Manuel Salas Velasco 15

16. Resultados
 Para contrastar la hipótesis de partida “A mayor cociente intelectual,
mayor nota en Matemáticas” debemos comprobar que el coeficiente
estimado b es estadísticamente significativo. ¿Cómo lo sabemos?
 Para que un coeficiente sea estadísticamente significativo el valor
obtenido en la columna “Probabilidad” (el llamado p-valor) debe ser menor
a 0,05; y que se cumple en nuestro caso
 (Nota: también si el valor del Estadístico t de student es superior en
valor absoluto a 2, que también se cumple)
 Una vez que hemos contrastado la hipótesis y sabemos que el CI explica
el rendimiento, con un 95% de confianza (100 - 0,05), la siguiente
pregunta que surge es: ¿cómo influye?
 En nuestra muestra, cuando aumenta el CI en una unidad, la nota en
matemáticas lo hace en 0,121 puntos
16Prof. Dr. Manuel Salas Velasco

17. R cuadrado
Prof. Dr. Manuel Salas Velasco 17
 R2 indica la proporción de variación de la variable dependiente
explicada por la variable independiente
 En nuestro caso, el 53,5% de la variación en el rendimiento escolar viene
explicada por la inteligencia
 R2 (o coeficiente de determinación) nos permite evaluar, en definitiva, la
bondad del ajuste (si el modelo se ajusta bien o mal a los datos)
 R2 toma valores entre 0 y 1
 Un R2 cercano a 1 indica un buen ajuste: los puntos quedan muy cerca del
modelo lineal ajustado (un valor alto para R2 es importante para que
nuestras predicciones sean fiables)
 En nuestro caso, una forma de incrementar el valor de R2 para mejorar el ajuste
y la fiabilidad de las predicciones es mediante la incorporación de más variables
independientes que expliquen el rendimiento escolar
 Si R2 fuese igual a 1, todas las observaciones caerían en la línea de
regresión por lo que el conocer X permite la predicción de Y sin error
 Un R2 cercano a 0 indica un mal ajuste (el modelo no nos sirve)

18. Ejercicio de predicción
La econometría es muy útil para
hacer predicciones
Si hemos comprobado que el CI
explica la NOTAMATE, y tenemos
un buen ajuste (nuestro R2 es
relativamente alto), entonces
podemos predecir la nota en
Matemáticas de un niño o una
niña no incluido/a en la muestra
Prof. Dr. Manuel Salas Velasco 18
CI0,1215,707-MATEANOT ˆ
Por ejemplo, ¿cuál sería la nota
esperada para un alumno o alumna
con un coeficiente intelectual de 95
(este/a alumno/a no está en la
muestra?
 
7885MATEANOT
950,1215,707-MATEANOT
,ˆ
ˆ

