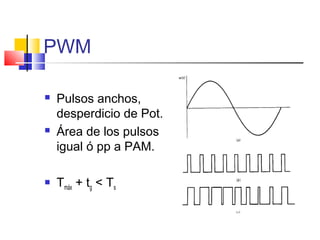
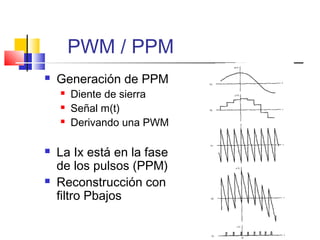
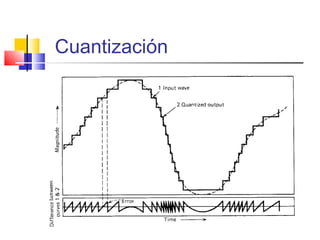
El documento aborda las ventajas y desventajas de los sistemas digitales y la modulación de pulsos, destacando aspectos como la inmunidad al ruido, la evolución de circuitos digitales y el proceso de muestreo. Se detallan diferentes técnicas de modulación, sus parámetros, y la importancia de la tasa de muestreo según el teorema de Nyquist para evitar problemas como el aliasing. También se menciona el proceso de reconstrucción de señales a partir de muestras, así como los requisitos de conversión y sincronización en sistemas digitales.

1. SISTEMAS DIGITALES
Ventajas

2. Ventajas – Sistemas digitales
 Inmunidad al ruido
 Estructura básica única (distintos tipos
de señales, algoritmo)
 Único circuito de procesamiento
(memorias)
 Posibilidad de evaluación de los
circuitos de procesamiento

3. Ventajas – Sistemas digitales
 Posibilidad de evaluación de los
circuitos de procesamiento
 Facilidad de los circuitos digitales para
tomar decisiones lógicas
 Integración de los bloques de
transmisión y conmutación (circuitos
telefónicos)

4. Ventajas
Regeneración de la señal
 Facilidad de reconocimiento de los
estados definidos
 Repetidores intermedios /
Regeneradores (imposible en sistemas
analógicos)
 Pe arbitrariamente pequeña (Proyecto /
especificación)

5. Ventajas – S/N - Señalización
 Funcionamiento con bajas relaciones
S/N (aproximadamente 20 dB)
 Facilidad de señalización.
 La información de control puede viajar
con los datos. Misma señalización para
distintos canales

6. Ventajas – Encriptado -
Gestión
 Posibilidad de inserción de encriptado.
 Facilidad de monitoreo de señales.
 Calidad de servicio (paràmetros
eléctricos)

7. Desventajas
 Mayor requerimiento de ancho de
banda de transmisión (4KHz)
 Necesidad de conversión A/D y D/A
 Necesidad de sincronización de
tiempos de clock Tx / Rx.
 Incompatibilidad con la red AAG
existente.

8. Modulación de Pulsos
Modulación AAG de pulsos.
 Portadora: Tren de pulsos
 Mensaje de onda continua
 Parámetros:
 Amplitud
 Duración
 Posición

9. Modulación Analógica de
Pulsos
• La señal mensaje se describe de forma
adecuada por sus valores muestras.
• Técnica de procesamiento del
mensaje
• Los parámetros de los pulsos varían de
forma continua

10. Modulación Analógica de Pulsos
 PAM – Pulse Amplitude Modulation
Modulación por amplitud de pulsos
 PWM – Pulse Wide Modulation
Modulación por ancho de pulso
 PPM – Pulse Position Modulation
Modulación por posición de pulsos

11. Analogías con sistemas AAG
 PAM AM
 PWM / PPM modulación
exponencial de onda continua

12. Modulación Analógica de
pulsos
 Gran contenido de CC y bajas frecuencias.
 Transmisión en distancias muy pequeñas.
 Es necesario modular una portadora de RF si
se quiere transmitir a mayores distancias
 No se usa para transmisión directa de
señales sino que forma parte del
procesamiento de la señal.

13. Modulación Analógica de
Pulsos
 Muestreo instantáneo de la señal mensaje
m(t) cada Ts segundos, fs = 1/Ts según el
Teorema de Muestreo
 Alargamiento de la duración de cada
muestra hasta un cierto valor constante T
 Muestreo y retención

14. Modulacion Digital de pulsos
 Representación de forma discreta,
tanto en el tiempo como en la amplitud
 Transmisión digital como una
secuencia de pulsos codificados (PCM)

15. Proceso de Muestreo
Muestreo de techo
plano
Una señal analógica se
convierte en una secuencia
de muestras
equiespaciadas
uniformemente en el tiempo
• Selección adecuada
del tiempo de muestreo
• La secuencia de
muestras define la señal
original de forma única

16. Proceso de Muestreo
 g(t): Señal arbitraria de energía finita
 {g(n Ts)} Secuencia de muestras
instantáneas de la señal g(t) a una
velocidad uniforme cada Ts segundos
 Ts: Período de muestreo
 fs = 1/ Ts : frecuencia de muestreo
 gδ(t): Señal ponderada por funciones δ

17. Proceso de Muestreo
 Señal muestreada de forma ideal

18. Proceso de Muestreo
 gδ(t) aproximarse por medio de un pulso
rectangular de duración:∆t y amplitud:
g(nTs)/∆t
 Cuanto más pequeño ∆t, mejor
aproximación
 Par transformado
 fs : Frecuencia de muestreo

19. Proceso de Muestreo
El proceso de muestrear
uniformemente una señal de
energía finita, en un tiempo
continuo, produce un espectro
periódico con un período igual a la
frecuencia de muestreo

20. Proceso de Muestreo
 Otra expresión de la transformada de
Fourier
Transformada de Fourier en
Tiempo Discreto
 g(t) de energía finita y duración infinita

21. Proceso de Muestreo
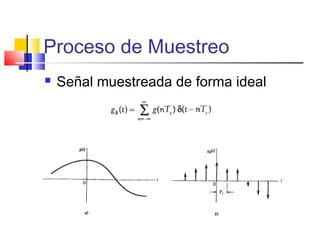
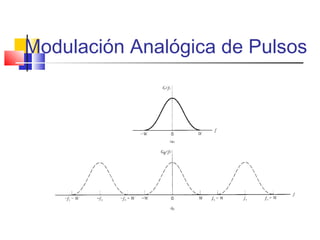
 g(t) estrictamente limitada en banda W
 G(f) no tiene componentes por encima
de W [Hz]
 Período de muestreo Ts =1/2W

22. Proceso de Muestreo

23. Proceso de Muestreo
 Transformada de Fourier en tiempo
discreto

24. Proceso de Muestreo
 g(t) se relaciona con G(f) a través de la
Transformada Inversa de Fourier.
 g(t) se puede obtener en forma única
mediante sus valores muestra g(n/2W)
para n variando desde –inf. a inf.
 La secuencia {g(n Ts)} tiene toda la
información contenida en g(t).

25. Reconstrucción de la señal
 Reconstrucción a partir de {g(n/2W)}

26. Reconstrucción de la señal
 Fórmula de interpolación para
reconstruir la señal a partir de valores
muestreados {g(n/2W)}, con la función
senc desempeñando el papel de la
interpolación
g(t)

27. Recordando: Teorema
Muestreo
Señales de banda limitada (W)
energia finita.
 Tx
Descripción con muestreo en t=1/2W
 Rx
Recuperación con muestras a una tasa
2W muestras/s

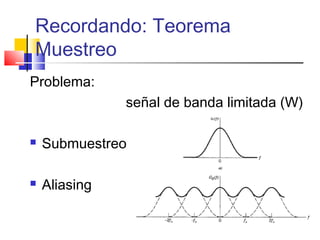
28. Recordando: Teorema
Muestreo
Para una señal de banda limitada (W)
 Tasa de muestreo ó frecuencia de
Nyquist: 2W muestras/s
 Intervalo de Nyquist t=1/2W [seg]

29. Recordando: Teorema
Muestreo
Problema:
señal de banda limitada (W)
 Submuestreo
 Aliasing

30. Recordando: Teorema Muestreo
Solución:
 Filtro pasabajos antialiasing (antes de
muestrear)
 Muestrear a una tasa un poco superior a
la tasa de Nyquist

31. Modulación Analógica de Pulsos

32. Recordando: Teorema
Muestreo
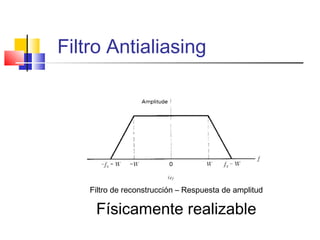
Filtro de Reconstrucción
 Filtro pasabajos Banda pasante [-W,W];
coincide con el filtro antialiasing
 Banda de transición [W, fs-W], fs tasa de
muestreo

33. Filtro Antialiasing
Filtro de reconstrucción – Respuesta de amplitud
Físicamente realizable

34. Modulación Analógica de
pulsos
 PAM: AMPLITUD
 T: Duración del pulso
 Ts: Tiempo entre muestras

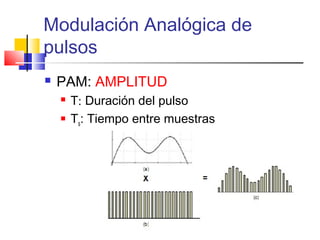
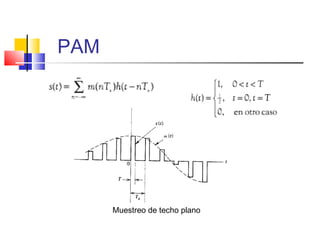
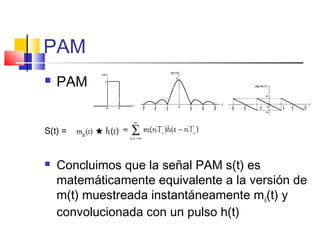
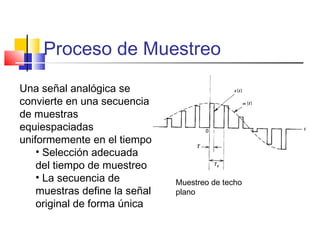
35. PAM
 Pulsos regularmente espaciados : Ts
 Pulsos rectangulares o de forma
apropiada [h(t)]
 Muestreo de techo plano

36. PAM
Dos operaciones involucradas
 Muestreo instantáneo de m(t) c/ Ts seg.,
de acuerdo al teorema del muestreo
 Duración del pulso: T= tiempo por el cual
se mantiene el valor muestra
SAMPLE AND HOLD

37. PAM
Muestreo de techo plano

38. PAM
 La versión muestreada
instantáneamente

39. PAM
 PAM
S(t) =
 Concluimos que la señal PAM s(t) es
matemáticamente equivalente a la versión de
m(t) muestreada instantáneamente mδ(t) y
convolucionada con un pulso h(t)

40. PAM
 Transformando esta expresión
 Cómo recuperamos la señal original
m(t)??

41. PAM
 Filtro de reconstrucción + ecualizador
 H(f) provoca distorsión de amplitud y
retardo de T/2. Se corrije ecualizando

42. PAM
 Recuperación de una señal PAM

43. Modulación Analógica de
pulsos
 El pulso modulado
varía en
proporción directa
a los valores
muestra.
 a) Mensaje (Mx)
 b) Clock
 c) PWM
 d) PPM

44. Modulación Analógica de
Pulsos
 En PAM y PWM
m(t)=0 se representan con un valor
paramétrico diferente de cero.
 Sincronización del Rx –
Multicanalización por división de tiempo

45. PWM
 Pulsos anchos,
desperdicio de Pot.
 Área de los pulsos
igual ó pp a PAM.
 Tmáx + tg < Ts

46. PWM / PPM
 Generación de PPM
 Diente de sierra
 Señal m(t)
 Derivando una PWM
 La Ix está en la fase
de los pulsos (PPM)
 Reconstrucción con
filtro Pbajos

47. COMPARACIÓN
 Dificultad circuital (mín): PAM
 Ancho de Banda:
 Piso: BB digital
 Techo: ISI
 Potencia transmitida (mín): PPM

48. COMPARACIÓN
 Costo: Asociado a la complejidad
circuital
 Inmunidad al ruido (máx): PPM

49. Cuantización