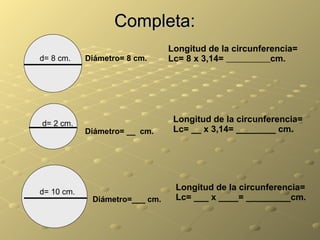
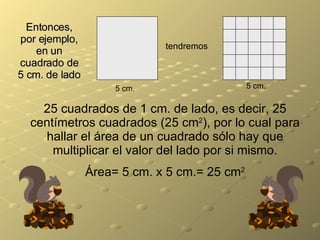
El documento explica conceptos básicos de geometría como perímetro, área, circunferencia y diferentes figuras geométricas. Define perímetro como la suma de los lados de un polígono y área como la medida de una superficie. Explica cómo calcular el perímetro de cuadrados, rectángulos y triángulos, así como el área de estas figuras. También cubre el cálculo de la longitud de una circunferencia a partir de su diámetro. Finalmente, proporciona ejemplos numéricos para practicar estos conceptos

1. Momento: EL BOSQUE Elemento: LA ARDILLA ¡Buenos días! La superficie del bosque yo recorro cada día, como es un área muy grande siempre encuentro compañía

2. ¿Sabes qué es el perímetro de una figura? ¿Has oído hablar del área de tu finca o de tu casa? ¿Cómo describirías la superficie de tu salón?

3. Las figuras geométricas siempre están a nuestro alrededor Cuando miramos una figura podemos detallar dos cosas diferentes: Su CONTORNO que es la línea o líneas que forman el borde, o la SUPERFICIE que está en su interior.

4. El contorno puede estar formado por líneas rectas solamente y la figura se llama POLÍGONO

5. Para medir el contorno de un polígono basta con sumar la medida de todos sus lados. A esta medida se le llama PERÍMETRO . Perímetro es la suma de TODOS los lados de un polígono 5 cm. 4 cm. 5 cm. 10 cm. P= 10+5+4+5 = 24 cm.

6. Calcula el perímetro de las siguientes figuras: 3 cm. 10 cm. 3 cm. 10 cm. P= P= P= 8 cm. 6 cm. 5 cm. 12 cm.

7. Lee con atención y responde: Si tienes un cuadrado con perímetro 20 cm., entonces cada lado mide a) 10 cm. b) 2 cm. c) 5 cm. d) 4 cm. En un rectángulo de perímetro 16 cm. y de ancho 3 cm., su lado más largo mide a) 13 cm. b) 5 cm. c) 2 cm. d) 10 cm. En un triángulo equilátero de perímetro 60 m, cada lado mide a) 20 cm. b) 30 cm. c) 10 cm. d) 15 cm.

8. Si el contorno de una figura es una circunferencia, no decimos perímetro, sino LONGITUD DE LA CIRCUNFERENCIA, y podemos calcularla midiendo su DIÁMETRO, que es la línea que por su centro la divide en dos partes iguales, y luego multiplicándolo por el número Pi ( π ), que los matemáticos han calculado aproximadamente en 3,14. d= 5 cm. Ej. Diámetro= 5 cm. Longitud de la circunferencia= Lc= 5 x 3,14= 15,70 cm.

9. Completa: d= 10 cm. Longitud de la circunferencia= Lc= ___ x ____= _________cm. Diámetro=___ cm. d= 8 cm. Diámetro= 8 cm. Longitud de la circunferencia= Lc= 8 x 3,14= cm. d= 2 cm. Longitud de la circunferencia= Lc= __ x 3,14= ________ cm. Diámetro= __ cm.

10. Miremos ahora el interior de las figuras planas Las superficies pueden ser duras como el piso, blandas como una espuma, lisas como el vidrio, ásperas como el pavimento, blancas como una pared o de muchos colores como un cuaderno, etc.

11. Escribe en tu cuaderno o en el programa Word del computador, qué características tienen las superficies de: El tablero del salón. El piso Tu pupitre. Las paredes. Las ventanas. Un cuaderno. Mira, toca, detalla su textura, color, dureza, brillo, etc. Muestra luego tu escrito al profesor.

12. Si ahora queremos medir las superficies, estaríamos hallando el ÁREA de ellas El área es la medida de una superficie ¿Cómo se hallaría esta medida? La verdad es que eso depende de cada figura

13. Primero hay que tomar una unidad de referencia para comparar (recuerda que medir es comparar). Dentro de nuestro sistema métrico decimal, la unidad principal es el metro cuadrado, que es la superficie encerrada en un cuadrado que mide un metro por cada lado. Área= 1 m 2 Área= 1 m 2 1 m 1 m 1 m 1 m

14. Dentro de los múltiplos más usados del metro cuadrado están los Kilómetros cuadrados (Km 2 ) y las Hectáreas (Ha) 1 Km 2 = 1’000.000 de metros cuadrados 1 Ha= 10.000 metros cuadrados Y el submúltiplo más empleado es el centímetro cuadrado (cm 2 ) 1 m 2 = 10.000 centímetros cuadrados

15. Entonces, por ejemplo, en un cuadrado de 5 cm. de lado tendremos 5 cm. 5 cm. 25 cuadrados de 1 cm. de lado, es decir, 25 centímetros cuadrados (25 cm 2 ), por lo cual para hallar el área de un cuadrado sólo hay que multiplicar el valor del lado por si mismo. Área= 5 cm. x 5 cm.= 25 cm 2

16. En un rectángulo se multiplica el largo por el ancho, que equivale a decir base por altura. Ej. 3 m. 8 m. Área= base x altura Área= 8 m x 3 m = 24 m 2 Un Triángulo tendrá la mitad del área del rectángulo, por lo que se multiplica la base por la altura y se divide entre dos Ej. 3 m. 8 m. Área= base x altura / 2 Área= 8 m x 3 m / 2 m= 12 m 2

17. Imagina que tienes un alambre de 40 cm. de largo. Si lo doblas formando un cuadrado, ¿cuál es el área y el perímetro de la figura? 40 cm. A= ________ A= ________ P= ________ P= ________ Si con el mismo alambre formaras un rectángulo de 15 cm. de largo, ¿cuál es ahora el área y el perímetro de la figura? 40 cm. Compara los resultados y escribe una gran conclusión, que compartirás con los compañeros y el profesor. Consigue un alambre y practica más con otras figuras.

18. ¿Cuánto vale una cortina de 6 metros de largo y 4 metros de ancho si cada metro cuadrado cuesta $12.500? a)100.000 b)25.000 c)200.000 d)300.000 Hoy aprendiste mucho. Sigue estudiando y practicando y nunca te canses de buscar lo mejor, Dios te bendiga, chao.