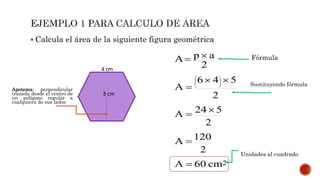
Este documento proporciona información sobre el perímetro y área de figuras geométricas. Explica las características de los polígonos y cómo calcular el perímetro y área de triángulos, cuadrados, circunferencias y otras figuras. También incluye ejemplos de cómo calcular el perímetro y área requeridos para proyectos como la construcción de un parque o un robot.