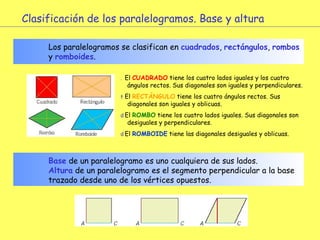
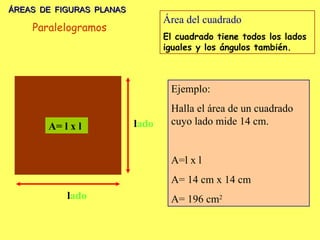
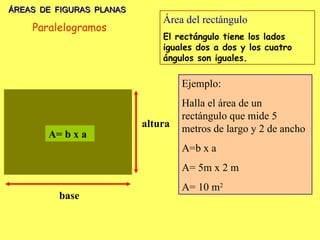
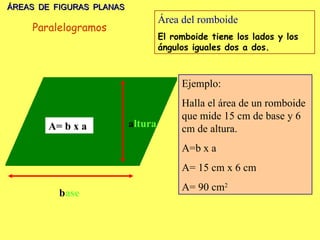
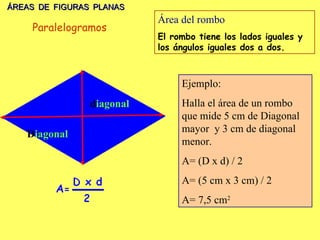
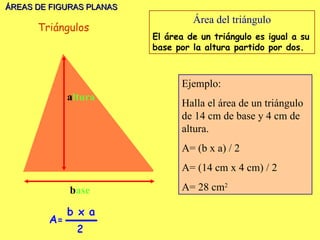
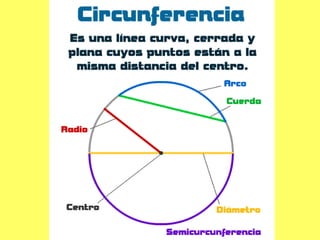
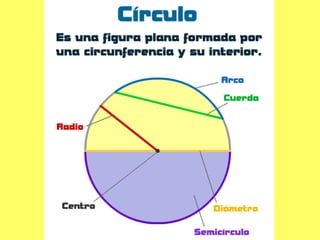
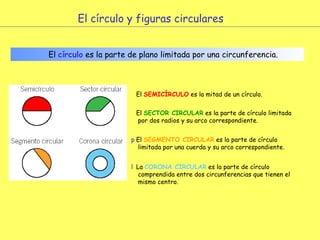
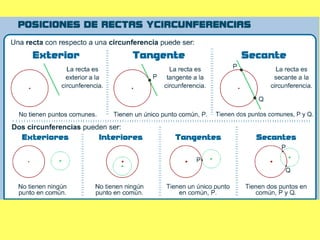
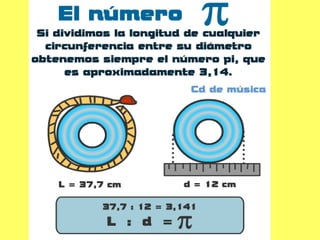
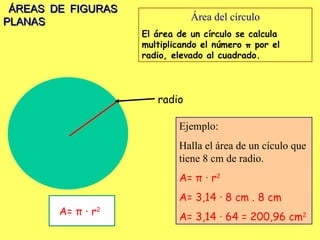
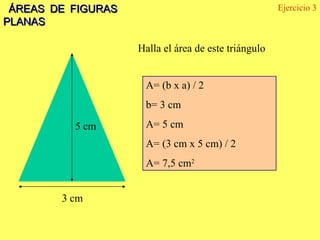
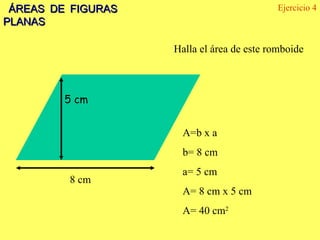
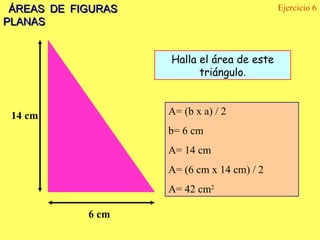
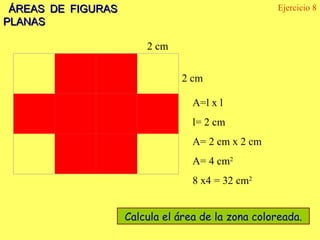
El documento explica los diferentes tipos de paralelogramos y cómo calcular el área de figuras planas como cuadrados, rectángulos, rombos, romboides y triángulos utilizando la fórmula del área (lado x lado, base x altura o mitad de la base por la altura). También describe círculos, sectores circulares y cómo calcular el área y longitud de la circunferencia de un círculo. El documento proporciona ejemplos numéricos de cada tipo de problema.

1. Áreas de figuras planas

2. Clasificación de los paralelogramos. Base y altura Los paralelogramos se clasifican en cuadrados , rectángulos , rombos y romboides .  El CUADRADO tiene los cuatro lados iguales y los cuatro ángulos rectos. Sus diagonales son iguales y perpendiculares. Base de un paralelogramo es uno cualquiera de sus lados. Altura de un paralelogramo es el segmento perpendicular a la base trazado desde uno de los vértices opuestos.  El RECTÁNGULO tiene los cuatro ángulos rectos. Sus diagonales son iguales y oblicuas.  El ROMBO tiene los cuatro lados iguales. Sus diagonales son desiguales y perpendiculares.  El ROMBOIDE tiene las diagonales desiguales y oblicuas.

3. ÁREAS DE FIGURAS PLANAS l ado l ado A= l x l Área del cuadrado El cuadrado tiene todos los lados iguales y los ángulos también. Ejemplo: Halla el área de un cuadrado cuyo lado mide 14 cm. A=l x l A= 14 cm x 14 cm A= 196 cm 2 Paralelogramos

4. ÁREAS DE FIGURAS PLANAS base altura A= b x a Área del rectángulo El rectángulo tiene los lados iguales dos a dos y los cuatro ángulos son iguales. Ejemplo: Halla el área de un rectángulo que mide 5 metros de largo y 2 de ancho A=b x a A= 5m x 2 m A= 10 m 2 Paralelogramos

5. ÁREAS DE FIGURAS PLANAS b ase a ltura A= b x a Área del romboide El romboide tiene los lados y los ángulos iguales dos a dos. Ejemplo: Halla el área de un romboide que mide 15 cm de base y 6 cm de altura. A=b x a A= 15 cm x 6 cm A= 90 cm 2 Paralelogramos

6. ÁREAS DE FIGURAS PLANAS D iagonal d iagonal Área del rombo El rombo tiene los lados iguales y los ángulos iguales dos a dos. Ejemplo: Halla el área de un rombo que mide 5 cm de Diagonal mayor y 3 cm de diagonal menor. A= (D x d) / 2 A= (5 cm x 3 cm) / 2 A= 7,5 cm 2 Paralelogramos

8. ÁREAS DE FIGURAS PLANAS b ase a ltura Área del triángulo El área de un triángulo es igual a su base por la altura partido por dos. Ejemplo: Halla el área de un triángulo de 14 cm de base y 4 cm de altura. A= (b x a) / 2 A= (14 cm x 4 cm) / 2 A= 28 cm 2 Triángulos

9. La circunferencia La circunferencia es una línea curva cerrada y plana en la que todos sus puntos están a igual distancia del centro.  El RADIO es el segmento que une el centro con un punto cualquiera de la circunferencia.  La CUERDA es un segmento que une dos puntos cualesquiera de la circunferencia.  El DIÁMETRO es una cuerda que pasa por el centro de la circunferencia.  El ARCO es la parte de circunferencia comprendida entre dos puntos cualesquiera.  La SEMICIRCUNFERENCIA es un arco igual a la mitad de la circunferencia.

12. El círculo y figuras circulares El círculo es la parte de plano limitada por una circunferencia.  El SEMICÍRCULO es la mitad de un círculo.  El SECTOR CIRCULAR es la parte de círculo limitada por dos radios y su arco correspondiente.  El SEGMENTO CIRCULAR es la parte de círculo limitada por una cuerda y su arco correspondiente.  La CORONA CIRCULAR es la parte de círculo comprendida entre dos circunferencias que tienen el mismo centro.

15. Longitud de la circunferencia. La longitud de la circunferencia se calcula multiplicando 2 por el número π y por el radio. ÁREAS DE FIGURAS PLANAS Ejemplo: Halla la longitud de una circunferencia que tiene 8 cm de radio. L= 2 x π x r L= 2 x 3,14 x 8 cm L= 2. 3,14 · 8 = 50,24 cm L= 2 x π x r

16. ÁREAS DE FIGURAS PLANAS Área del círculo El área de un círculo se calcula multiplicando el número π por el radio, elevado al cuadrado. A= π · r 2 Ejemplo: Halla el área de un cículo que tiene 8 cm de radio. A= π · r 2 A= 3,14 · 8 cm . 8 cm A= 3,14 · 64 = 200,96 cm 2 radio

17. ÁREAS DE FIGURAS PLANAS Halla el área de este cuadrado Ejercicio 1 A=l x l l= 5 cm A= 5 cm x 5 cm A= 25 cm 2

18. ÁREAS DE FIGURAS PLANAS Halla el área de un rectángulo de base 7 cm y altura 2,5 cm. Ejercicio 2 A=b x a b= 7 cm a= 2,5 cm A= 7cm x 2,5 cm A= 17,5 cm 2

19. ÁREAS DE FIGURAS PLANAS 5 cm 3 cm Halla el área de este triángulo Ejercicio 3 A= (b x a) / 2 b= 3 cm A= 5 cm A= (3 cm x 5 cm) / 2 A= 7,5 cm 2

20. ÁREAS DE FIGURAS PLANAS Ejercicio 4 5 cm 8 cm Halla el área de este romboide A=b x a b= 8 cm a= 5 cm A= 8 cm x 5 cm A= 40 cm 2

21. ÁREAS DE FIGURAS PLANAS Ejercicio 5 24 cm 10 cm Calcula el área del rombo. A= (D x d) / 2 D= 24 cm d= 10 cm A= (24 cm x 10 cm) / 2 A= 120 cm 2

22. ÁREAS DE FIGURAS PLANAS Ejercicio 6 14 cm 6 cm Halla el área de este triángulo . A= (b x a) / 2 b= 6 cm A= 14 cm A= (6 cm x 14 cm) / 2 A= 42 cm 2

23. ÁREAS DE FIGURAS PLANAS Ejercicio 8 2 cm 2 cm Calcula el área de la zona coloreada. A=l x l l= 2 cm A= 2 cm x 2 cm A= 4 cm 2 8 x4 = 32 cm 2

24. ÁREAS DE FIGURAS PLANAS Ejercicio 9 10 cm. Calcula el área de este circulo y la longitud de su circunferencia A= π · r 2 A= 3,14 · 10 cm . 10 cm A= 3,14 · 100 = 314 cm 2 L= 2 x π x r L= 2 x 3,14 x 10 cm L= 2. 3,14 · 10 = 62,28 cm