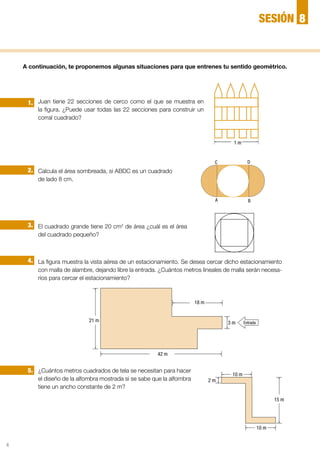
El documento presenta cuatro diseños de parterres para un jardín y se pregunta si es posible construir una valla alrededor de cada diseño usando 32 metros de madera. Se pide analizar cada diseño y determinar si se puede o no construir la valla, además de hacer preguntas para comprender mejor los conceptos geométricos involucrados como área y perímetro.

1. 1
Un carpintero tiene 32 metros de madera y quiere construir una pequeña valla alrededor de un
parterre en el jardín. Está considerando los siguientes diseños para el parterre.
Encierra en un círculo “Sí” o “No” para indicar si, para cada diseño, se puede o no se puede
construir la valla con los 32 metros de madera.
Diseño del parterre ¿Puede construirse la valla?
Diseño A Sí / No
Diseño B Sí / No
Diseño C Sí / No
Diseño D Sí / No
Hagamos preguntas para comprender mejor:
¿Qué es un parterre?
¿Qué es lo que desea hacer el carpintero?
¿Qué medida geométrica te puede ayudar en este caso?
Diseño A
¿Es necesario tener las medidas de los pequeños segmentos para responder? Explica.
¿Cuál es valor de longitud total de los segmentos horizontales superiores?
¿Cuál es valor de longitud total de los segmentos verticales?
¿Es posible construir la valla?
Diseño B
¿Cada lado inclinado mide más, menos o igual a 6 m? Explica.
¿Saber lo anterior te ayuda a decidir?
¿Es posible construir la valla?
Diseño C
¿Es este caso análogo al Diseño A? Explica.
¿El método usado en A, te puede ayudar en este caso?
¿Es posible construir la valla?
Diseño D
¿Es posible construir la valla?
¿Cuál de las figuras tiene mayor área?
Enlacarpintería1
Conexiones
8SESIÓN
FICHA DE MATEMÁTICA
1
Texto adaptado para fines didácticos. Fuente: OCDE (2013). “Carpintero”. En INSTITUTO NACIONAL DE EVALUACIÓN EDUCATIVA. Estímulos PISA de matemáticas liberados.
Madrid: Inee, pp. 223-225.
A.
C.
B.
D.
6 m
10 m
10 m
6 m
10 m
6 m
10 m
6 m

2. 2
Estanterías2
Para construir una repisa un carpintero necesita lo siguiente:
4 tablas largas de madera, 6 tablas cortas de madera, 12
ganchos pequeños, 2 ganchos grandes, 14 tornillos.
El carpintero tiene en el almacén 26 tablas largas de made-
ra, 33 tablas cortas de madera, 200 ganchos pequeños, 20
ganchos grandes y 510 tornillos.
¿Cuántas repisas completas puede construir este carpin-
tero?
Hagamos preguntas para comprender mejor:
— ¿Qué es una repisa?
— ¿El dibujo mostrado cumple con las especificaciones dadas en el texto?
Organicemos los datos en una tabla:
N.º de repisa Tablas largas Tablas cortas Ganchos p Ganchos g Tornillos
1 4 6 12 2 14
N.º de repisa Tablas largas Tablas cortas Ganchos p Ganchos g Tornillos
26 33 200 20 510
N.º de repisa Tablas largas Tablas cortas Ganchos p Ganchos g Tornillos
6 24 36
N.º de repisa Tablas largas Tablas cortas Ganchos p Ganchos g Tornillos
¿Qué tenemos en el almacén?
Una estrategia es hacer crecer proporcionalmente la tabla inicial.
Si multiplico por 6 para alcanzar las 26 tablas largas tengo:
No sigo pues no tengo 36 tablas cortas. Entonces multiplico por un número menor:
¿Cuántas repisas puede hacer?
8SESIÓN
2
Texto adaptado para fines didácticos. Fuente: OCDE (2013). “Estanterías”. En INSTITUTO NACIONAL DE EVALUACIÓN EDUCATIVA. Estímulos PISA de matemáticas liberados.
Madrid: Inee, pp. 30-31.

3. 3
La vida cotidiana está llena de formas, aunque en realidad todas las formas son tridimensionales.
En numerosas ocasiones idealizamos las formas para trabajarlas de manera plana, por ejemplo
una hoja de papel en realidad es un prisma, aunque su altura sea solo el diminuto espesor de
la hoja de papel. Sin embargo, cuando hablamos del área de la hoja, nos referimos al área de
cualquiera de las dos superficies grandes del prisma. En general, utilizamos el lenguaje coloquial
combinado con conocimientos matemáticos para poder describir temas geométricos.
Si recorres con tu mirada el salón observarás que existen muchas figuras rectilíneas: rectángulos,
cuadrados, líneas horizontales y verticales, claro que también encontrarás formas curiosas como
las elipses o las parábolas, pero esos temas serán motivo de un estudio posterior en la escuela.
Dada la gran presencia de formas elementales en la cotidianidad, conviene que sepas algunos
conceptos importantes:
— El perímetro de una figura es. Es la suma de las longitudes del borde de la figura.
— En el caso de un cuadrado de lado a el perímetro es 4a, en el caso de un rectángulo de lados
a y b el perímetro es 2(a+b), el perímetro de una circunferencia de radio r es 2πr.
— Las unidades del perímetro son de longitud, es decir: metros, decímetros, pulgadas, centíme-
tros, pasos, entre otras unidades de longitud.
— Toda figura plana cerrada tiene perímetro, para medirlo solo basta rodear con una cuerda su
contorno y luego medir la cuerda.
— El área es otro concepto importante y es la medida de la superficie de una región plana, entre
las fórmulas más comunes se encuentran las siguientes:
Cuadrado Rectángulo Paralelogramo Círculo
a2
ab bh πr2
Cubo Cilindro Cono Esfera
a3
πr2
h πr2
h πr3
— El área de una figura se mide en unidades cuadradas de longitud: es decir m2
, pg2
, km2
, etc.
— El área de una figura compleja se puede obtener por descomposición en partes más pequeñas.
— Otro concepto de utilidad es el volumen. En general, en el día a día usamos cubos, cilindros,
cascos esféricos, conos rectos, entre otros.
— El volumen es la medida de la capacidad de un cuerpo. Los volúmenes que deben conocer son:
1
3
4
3
a a
b
b
b
b
b
a
a
a
a
a
a
a
8SESIÓN
Herramientas matemáticas: cálculos geométricos
h
r
r
h h
r
r

4. 4
Juan tiene 22 secciones de cerco como el que se muestra en
la figura. ¿Puede usar todas las 22 secciones para construir un
corral cuadrado?
Calcula el área sombreada, si ABDC es un cuadrado
de lado 8 cm.
El cuadrado grande tiene 20 cm2
de área ¿cuál es el área
del cuadrado pequeño?
La figura muestra la vista aérea de un estacionamiento. Se desea cercar dicho estacionamiento
con malla de alambre, dejando libre la entrada. ¿Cuántos metros lineales de malla serán necesa-
rios para cercar el estacionamiento?
¿Cuántos metros cuadrados de tela se necesitan para hacer
el diseño de la alfombra mostrada si se sabe que la alfombra
tiene un ancho constante de 2 m?
2.
1.
3.
4.
5.
A continuación, te proponemos algunas situaciones para que entrenes tu sentido geométrico.
18 m
21 m 3 m Entrada
42 m
15 m
10 m
2 m
10 m
1 m
A
C
B
D
8SESIÓN

5. 5
Escaleras3
Las figuras4
El esquema siguiente ilustra una escalera con 14 peldaños y una altura total de 252 cm.
a. ¿Cuál de las figuras tiene mayor área? Muestra tu razonamiento.
b. Describe un método para hallar el área de la figura C.
c. Describe un método para hallar el perímetro de la figura C.
¿Cuál es altura de cada uno de los 14 peldaños?
Solución
Solución
Como hay 14 peldaños, entonces hay 14 segmentos horizontales, análoga-
mente hay 14 segmentos verticales.
Sabemos que la altura total es de 252 cm, por tanto para saber la medida del
alto de cada peldaño dividimos.
a. Por comparación, si imaginamos que tomo la figura B y la monto sobre
la figura A, observo que es mayor, lo mismo ocurrirá si la coloco sobre C.
Luego la figura B es la de mayor área. También podía haber decidido por
la B porque no tiene hendiduras que hacen decrecer el área y A y C tienen
huecos o porque B es un círculo completo, y las otras figuras parecen cír-
culos con trozos extraídos.
b. Puedo dividir el área en partes. El centro de la figura puede ser un cuadrado
y cada brazo puedo aproximarlo a un rectángulo.
c. Si rodeo la figura con un hilo y luego mido el hilo obtendré el perímetro de la
figura C.
Entonces cada peldaño tiene una altura de 18 cm.
=
252
14
18
cm
cm
Altura total 252 cm
A B C
8SESIÓN
Matemática en contexto
3
Texto adaptado para fines didácticos. Fuente: OCDE (2013). “Escalera”. En INSTITUTO NACIONAL DE EVALUACIÓN EDUCATIVA. Estímulos PISA de matemáticas liberados.
Madrid: Inee, pp. 161-162.
4
Texto adaptado para fines didácticos. Fuente: OCDE (2013). “Las figuras”. En INSTITUTO NACIONAL DE EVALUACIÓN EDUCATIVA. Estímulos PISA de matemáticas liberados.
Madrid: Inee, pp. 163-164.
Profundidad total 400 cm

6. 6
Encierra en un círculo la única figura que re-
presenta la siguiente descripción. El triángulo
PQR es un triángulo rectángulo con el ángulo
recto en R. El segmento RQ es menor que el
segmento PR. M es el punto medio del seg-
mento PQ y N es el punto medio de QR. S
es un punto dentro del triángulo. El segmento
MN es más grande que el segmento MS.
¿En qué vértice está el ángulo recto?
¿El punto S dónde se encuentra?
Este es el plano del apartamento que los padres de Jorge quieren comprar a una agencia
inmobiliaria.
Para calcular la superficie (área) total del
apartamento (incluidas la terraza y las paredes)
puedes medir el tamaño de cada habitación,
calcular la superficie de cada una y sumar todas
las superficies.
No obstante, existe un método más eficaz para
calcular la superficie total en el que solo tienes que
medir 4 longitudes.
Señala en el plano anterior las cuatro longitudes
necesarias para calcular la superficie total del
apartamento.
Esquematiza el problema.
¿Qué longitudes necesitas para calcular el
área de un rectángulo?
Este es el plano de la heladería de María. Ella
está renovando la tienda. El área de servicio
está rodeada por el mostrador.
María quiere colocar un nuevo borde a lo largo
de la parte externa del mostrador. ¿Cuál es la
longitud total del borde que necesita? Escribe
tus cálculos.
Nota: Cada cuadrado de la cuadrícula repre-
senta 0,5 metros.
Nicolás quiere pavimentar el patio rectangular de su nueva casa. El patio mide 5,25 metros de
largo y 3,00 metros de ancho. Nicolás necesita 81 ladrillos por metro cuadrado. Calcula cuántos
ladrillos necesita Nicolás para pavimentar todo el patio.
1.
2.
3.
4.
Baño
Salón
Terraza
Escala:
1 cm representa 1 m
Dormitorio
Cocina
P
M
Q
SR
N
P
Q
M
N R
S
M
P
S
Q RN
PQ M
N
R
S
M
P
S
Q
R
N
A
C D
E
B
8SESIÓN
Manos a la obra Tiempo: 25 minutos
Puerta de entrada
Entrada
Mostrador
Área de servicio
Área de mesas