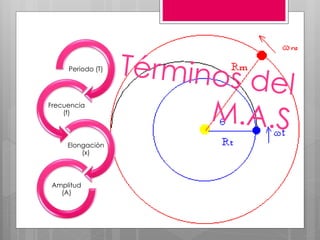
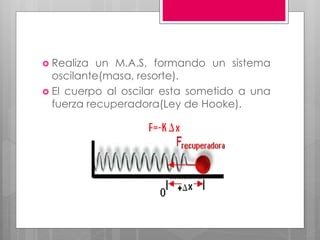
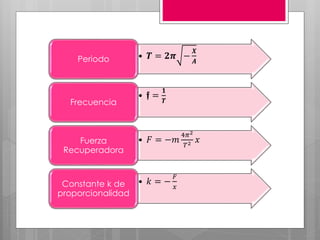
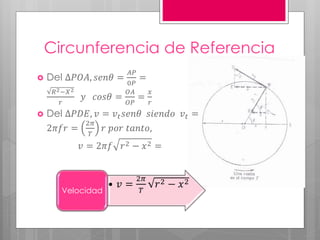
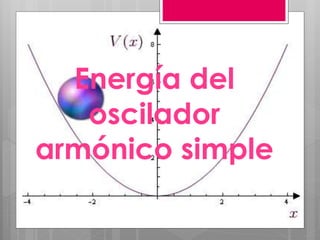
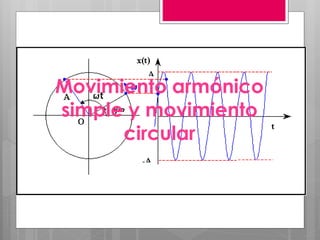
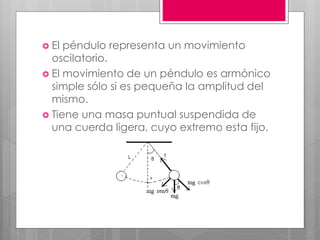
Este documento describe el movimiento oscilatorio armónico simple y sus características fundamentales. Explica que un movimiento oscilatorio ocurre cuando una partícula se mueve periódicamente respecto a una posición de equilibrio debido a una fuerza recuperadora proporcional a su desplazamiento. Define conceptos clave como periodo, frecuencia, amplitud y elongación. También describe oscilaciones amortiguadas y forzadas, y fenómenos como resonancia.

1. MOVIMIENTO
OSCILATORIO
GRUPO 1
INTEGRANTES:
 Cindy Jazmín Guamán Tandazo.
 Soraya Vanessa Ojeda Carrión.
 Ariana Yadira Oñate Paladines.
 Andrés Angamarca Shinin.

3. INTRODUCCIÓN:
Es uno de los movimientos más importantes.
Una partícula oscila cuando se mueve
periódicamente respecto a una posición de
equilibrio.
De todos los movimientos oscilatorios, el más
importante es el movimiento armónico
simple (MAS), debido a que es una
aproximación a muchas oscilaciones presentes
en la naturaleza

5. Es un movimiento periódico, oscilatorio y
vibratorio en ausencia de fricción,
producido por la acción de una fuerza
recuperadora que es directamente
proporcional al desplazamiento pero en
sentido opuesto.

6. Periodo (T)
Frecuencia
(f)
Elongación
(x)
Amplitud
(A)

7. Movimiento de un
cuerpo unido a un
resorte.

8.  Realiza un M.A.S, formando un sistema
oscilante(masa, resorte).
 El cuerpo al oscilar esta sometido a una
fuerza recuperadora(Ley de Hooke).

9. Al estirar el resorte, se produce una fuerza
de deformación dirigida hacia la derecha,
mientras que se ejerce una fuerza
recuperadora en la masa hacia la
izquierda,

10. Representación
matemática del
M.A.S

11. • 𝑻 = 𝟐𝝅 −
𝑿
𝑨Periodo
• 𝖋 =
𝟏
𝑻Frecuencia
• 𝐹 = −𝑚
4𝜋2
𝑇2 𝑥Fuerza
Recuperadora
• 𝑘 = −
𝐹
𝑥Constante k de
proporcionalidad

12. Circunferencia de Referencia
 Del ∆𝑃𝑂𝐴, 𝑠𝑒𝑛𝜃 =
𝐴𝑃
0𝑃
=
𝑅2−𝑋2
𝑟
𝑦 𝑐𝑜𝑠𝜃 =
𝑂𝐴
𝑂𝑃
=
𝑥
𝑟
 Del ∆𝑃𝐷𝐸, 𝑣 = 𝑣 𝑡 𝑠𝑒𝑛𝜃 𝑠𝑖𝑒𝑛𝑑𝑜 𝑣 𝑡 =
2𝜋𝑓𝑟 =
2𝜋
𝑇
𝑟 𝑝𝑜𝑟 𝑡𝑎𝑛𝑡𝑜,
𝑣 = 2𝜋𝑓 𝑟2 − 𝑥2 =
• 𝑣 =
2𝜋
𝑇
𝑟2 − 𝑥2
Velocidad

13.  Siendo r el radio de la circunferencia y
amplitud del m.a.s
 Del ∆𝑃𝐵𝐶, 𝑎 = 𝑎 𝑐 𝑐𝑜𝑠𝜃 𝑠𝑖𝑒𝑛𝑑𝑜 𝑎 𝑐 =
𝑣2 𝑡
𝑟
=
4𝜋𝑟2 𝑓2 𝑟 = (
4𝜋𝑟2
𝑇2 ). De donde
𝑎 = −4𝜋2 𝑓2 𝑥 =
• 𝛼 = −
4𝜋2
𝑇2 𝑥Aceleración

14. Energía del
oscilador
armónico simple

15.  La fuerza ejercida por un resorte,
conserva la energía mecánica total.
 La energía mecánica total esta
relacionada directamente con la
amplitud (A) del movimiento.
 Formula:
𝐸 =
1
2
𝑘𝐴2

16. Movimiento armónico
simple y movimiento
circular

17.  El M.A.S y el M.C, tienen una relación
matemática dada por:
“La proyección sobre una recta de una
partícula que se mueve con movimiento
circular uniforme es un movimiento
armónico simple”.

18. Consideremos una partícula
que se mueve con una
velocidad constante sobre un
circunferencia de radio A
Velocidad angular es
constante por tanto:
𝜔∆= 𝑣
𝐴
El desplazamiento angular
esta dado por:
𝜃 = 𝜔𝑡 + 𝛿
Donde 𝛿 es el desplazamiento
angular en el instante t = 0.
Entonces:
x = A cos q = A cos (wt + d)
Finalmente:
La frecuencia y el período del
movimiento circular y
movimiento armónico simple,
son los mismos.

19. El
Péndulo

20.  El péndulo representa un movimiento
oscilatorio.
 El movimiento de un péndulo es armónico
simple sólo si es pequeña la amplitud del
mismo.
 Tiene una masa puntual suspendida de
una cuerda ligera, cuyo extremo esta fijo.

21. El
péndulo
Péndulo
Simple
Péndulo
Físico

22.  El péndulo simple es un sistema
idealizado constituido por una partícula
de masa, suspendida de un punto fijo
mediante un hilo inextensible y sin peso.
 El péndulo simple o matemático se
denomina así en contraposición.
Periodo de péndulo simple:
𝑇 = 2𝜋
𝑙
𝑔

23.  Un péndulo físico oscila como si su masa
estuviera concentrada en un solo punto a
una distancia l del centro de suspensión.
 Al desplazarse una partícula desde el
reposo hacia un ángulo (pequeño) con
la vertical y se la suelta, el péndulo
comienza a oscilar.
 Se utiliza para medir el tiempo, medir la
intensidad de la gravedad,
etc.

24. Oscilaciones
Amortiguadas

25. Definición…
 Es un movimiento que al disiparse la
energía mecánica debido a una fuerza
de fricción, la energía mecánica del
movimiento oscilante disminuye con el
tiempo .
 Una fuerza de amortiguamiento es
aquella que la considera proporcional a
la velocidad de la masa pero en sentido
opuesto en donde b es una constante
que describe el grado de
amortiguamiento.
𝐹𝑎 = −𝑏𝑣

26. Clases de Oscilaciones
Amortiguadas
AMORTIGUAMIENTO DEBIL
AMORTIGUAMIENTO
CRITICO
SOBREAMORTIGUAMIENTO

27. AMORTIGUAMIENTO DEBIL
Cuando la fuerza disipativa es
pequeña con respecto a la fuerza
de restitución, el carácter
oscilatorio del movimiento se
conserva pero la amplitud de la
vibración disminuye con el tiempo
y, el movimiento cesará. En el
movimiento con una constante
de resorte y una partícula, las
oscilaciones se amortiguan con
más rapidez a medida que el
valor máximo de la fuerza
disipativa tiende al valor máximo
de la fuerza de restitución.
.
AMORTIGUAMIENTO
CRITICO
Si el amortiguamiento del
oscilador aumenta
suficientemente, puede
llegar a alcanzar un valor
crítico e las oscilaciones
amortiguadas.
Evidentemente, en estas
condiciones no hay
oscilaciones y el oscilador
regresará a la posición de
equilibrio sin rebasarla solo
una vez.
SOBREAMORTIGUAMIENTO
Se presenta cuando esta
bajo ciertas condiciones,
en las cuales no habrá
oscilaciones, y la partícula
regresará a la posición de
equilibrio sin rebasarla mas
de una vez. Cuanto mayor
sea el amortiguamiento
más tiempo empleará el
sistema en quedar en
reposo en la posición de
equilibrio.

28. Oscilaciones
Forzadas

29.  La energía de un oscilador amortiguado
disminuye con el tiempo, como resultado de
una fuerza. Es posible compensarla
aplicando una fuerza externa que suministre
energía disipada realizando un trabajo sobre
el sistema.
 El oscilador forzado, está sometido a una
fuerza restauradora y a una fuerza externa
que varía armónicamente con el tiempo
Amplitud:
𝐴 =
𝐹𝑚𝑎𝑥
𝑘 − 𝑚𝜔
2
𝑑
2
+ 𝑏2 𝜔
2
𝑑

30.  Se define la frecuencia natural de un oscilador
como la que tendría si no estuviesen presentes ni
el amortiguamiento ni el sistema impulsor.
 El fenómeno de resonancia se produce cuando la
frecuencia impulsora es igual a la frecuencia
natural del sistema.

31. Estas curvas reciben el nombre
de curvas de resonancia.
Cuando el amortiguamiento es
pequeño (el valor de Q es alto),
la potencia consumida en la
resonancia es mayor y es más
aguda; la curva es más estrecha,
que quiere decir que la potencia
suministrada es grande cerca de
la frecuencia de resonancia.
Cuando el amortiguamiento es
grande (el valor de Q es
pequeño), la curva de
resonancia es más achatada y la
potencia suministrada toma
valores más para w diferentes de
la de resonancia.

32. Bibliografía:
• Movimiento armónico simple.
Wikipedia.com de
http://es.wikipedia.org/wiki/Movimien
to_arm%C3%B3nico_simple
• ESTUDIO DE LA DINÁMICA DEL M.A.S
teleformacion.edu.aytolacoruna.es
de
http://teleformacion.edu.aytolacorun
a.es/FISICA/document/fisicaInteractiv
a/mas/dinamica/MAS_dinamica.htm
• Movimiento armónico simple .FISICA
GENERAL. DANIEL SHAUM.SEXTA
EDICION .pág.. 83
• Energía del oscilador armónico
simple. Física Universitaria.
Semansky. Volumen 1.
Decimosegunda edición .pág.
429.
• Tema 1 : Movimiento Oscilatorio.
Dpto. Física Aplicada III
Universidad de Sevilla. De
http://www.esi2.us.es/DFA/FFII/A
puntes/Curso0910/1_Oscilacione
s_0910.pdf