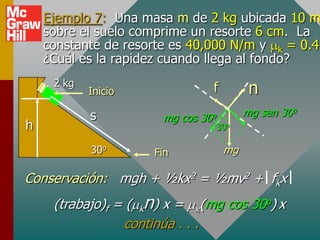
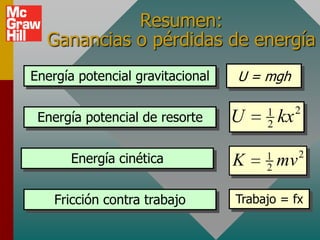
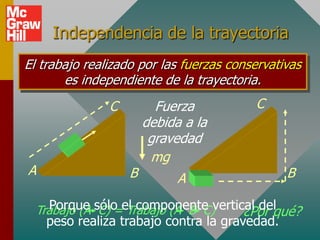
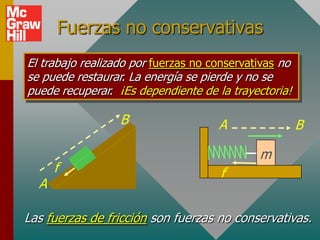
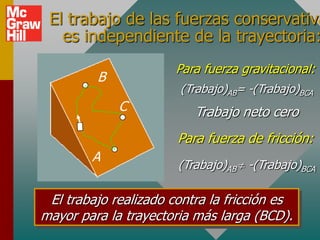
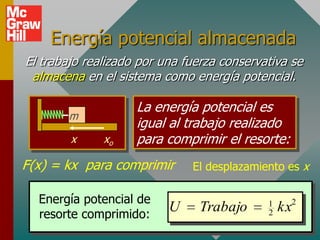
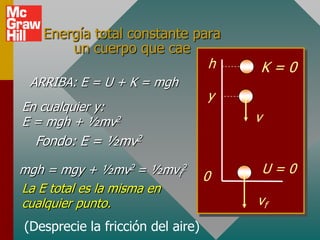
El documento presenta conceptos clave sobre la conservación de energía, incluyendo energía potencial, fuerzas conservativas y no conservativas, y la aplicación del principio de conservación de energía mecánica a varios ejemplos. Define energía potencial como la habilidad para realizar trabajo debido a la posición, y fuerzas conservativas como aquellas que realizan trabajo cero en un viaje redondo. Explica que la suma de la energía potencial y cinética es constante para sistemas conservativos en ausencia de fricción.

1. Conservación de energía
Presentación PowerPoint de
Paul E. Tippens, Profesor de Física
Southern Polytechnic State University

2. Una cascada en el
Parque Yellowstone
proporciona un
ejemplo de energía
en la naturaleza. La
energía potencial
del agua en la cima
se convierte en
energía cinética en
el fondo.

3. Objetivos: Después de completar
este módulo, deberá:
• Definir y dar ejemplos de fuerzas
conservativas y no conservativas.
• Definir y aplicar el concepto de
conservación de energía mecánica para
fuerzas conservativas.
• Definir y aplicar el concepto de
conservación de energía mecánica que
explique las pérdidas por fricción.

4. Energía potencial
La energía potencial es la habilidad para realizar
trabajo en virtud de la posición o condición.
Ejemplo: Una masa que se
m mantiene a una distancia h sobre
la Tierra.
h Si se libera, la Tierra puede
mg realizar trabajo sobre la masa:
Trabajo = mgh
Tierra
¿Este trabajo es + o - ?
¡Positivo!

5. Energía potencial gravitacional
La energía potencial gravitacional U es igual al
trabajo que se puede realizar POR la gravedad
debido a la altura sobre un punto específico.
U = mgh E.P. gravitacional
Ejemplo: ¿Cuál es la energía potencial cuando un
bloque de 10 kg se sostiene a 20 m sobre la calle?
U = mgh = (10 kg)(9.8 m/s2)(20 m)
U = 1960 J

6. El origen de la energía potencial
La energía potencial es una propiedad del
sistema Tierra-cuerpo. Ninguno tiene
energía potencial sin el otro.
F El trabajo realizado
por la fuerza de
h elevación F
mg
proporciona energía
potencial positiva,
mgh, al sistema
Tierra-cuerpo.
Sólo fuerzas externas pueden agregar o quitar energía.

7. Fuerzas conservativas
Una fuerza conservativa es aquella que hace
trabajo cero durante un viaje redondo.
El peso es conservativo.
F
El trabajo realizado por la
h
mg Tierra en el viaje hacia
arriba es negativo, - mgh
El trabajo de regreso
es positivo, +mgh
Trabajo neto = - mgh + mgh = 0

8. La fuerza de resorte
La fuerza ejercida por un resorte F
también es conservativa. x
m
Cuando se estira, el resorte
realiza trabajo negativo, - ½kx2.
Al liberarse, el resorte realiza
trabajo positivo, + ½kx2 x F
m
Trabajo neto = 0 (conservativa)

9. Independencia de la trayectoria
El trabajo realizado por las fuerzas conservativas
es independiente de la trayectoria.
C Fuerza C
debida a la
gravedad
mg
A B B
A
Trabajo (A sólo el componente vertical del
Porque C) = Trabajo (A B C) ¿Por qué?
peso realiza trabajo contra la gravedad.

10. Fuerzas no conservativas
El trabajo realizado por fuerzas no conservativas no
se puede restaurar. La energía se pierde y no se
puede recuperar. ¡Es dependiente de la trayectoria!
B A B
m
f f
A
Las fuerzas de fricción son fuerzas no conservativas.

11. El trabajo de las fuerzas conservativa
es independiente de la trayectoria:
Para fuerza gravitacional:
B
(Trabajo)AB= -(Trabajo)BCA
C Trabajo neto cero
Para fuerza de fricción:
A
(Trabajo)AB -(Trabajo)BCA
El trabajo realizado contra la fricción es
mayor para la trayectoria más larga (BCD).

12. Energía potencial almacenada
El trabajo realizado por una fuerza conservativa se
almacena en el sistema como energía potencial.
La energía potencial es
m
igual al trabajo realizado
x xo para comprimir el resorte:
F(x) = kx para comprimir El desplazamiento es x
Energía potencial de
resorte comprimido:
U Trabajo 1
2 kx2

13. Conservación de energía
(Fuerzas conservativas)
En ausencia de fricción, la suma de las energías
potencial y cinética es una constante, siempre
que no se agregue energía al sistema.
h v=0 En lo alto: Uo = mgh; Ko = 0
y mg En y: Uo = mgy; Ko = ½mv2
v
En y=0: Uo = 0; Ko = ½mvf 2
0
E = U + K = Constante
vf

14. Energía total constante para
un cuerpo que cae
h K=0
ARRIBA: E = U + K = mgh
y
En cualquier y:
E = mgh + ½mv2 v
Fondo: E = ½mv2
mgh = mgy + ½mv2 = ½mvf2 U=0
0
La E total es la misma en
cualquier punto. vf
(Desprecie la fricción del aire)

15. Ejemplo 1: Una bola de 2 kg se libera desde
una altura de 20 m. ¿Cuál es su velocidad
cuando su altura disminuye a 5 m?
20m v=0
Earriba total = E total a 5 m
mgh = mgy + ½mv2
5m
2gh = 2gy + v2
v
0
v2 = 2g(h - y) = 2(9.8)(20 - 5)
v= (2)(9.8)(15) v = 17.1 m/s

16. Ejemplo 2: Una montaña rusa cae de una
altura máxima de 100 ft. ¿Cuál es la
rapidez cuando llega a su punto más bajo?
Suponga fricción cero:
Arriba: U + K = mgh + 0
Abajo: U + K = 0 + ½mv2
La energía total se conserva
mgh = ½mv2 v = 2gh
v= (2)(32 ft/s2)(100 ft) v = 80 ft/s

17. Conservación de energía en
ausencia de fuerzas de fricción
La energía total es constante para un sistema
conservativo, como la gravedad o un resorte.
Comienzo: (U + K)o = Fin: (U + K)f
¿Altura? mgho mghf ¿Altura?
¿Resorte? ½kxo2 = ½kxf2 ¿Resorte?
¿Velocidad? ½mvo2 ½mvf2 ¿Velocidad?

18. Ejemplo 3. El agua en el fondo de una cascada tien
una velocidad de 30 m/s después de caer 35 ft.
¿Cuál es la rapidez del agua
en lo alto de la cascada?
ho = 35 m; vf = 30 m/s2
Primero observe el punto de inicio: lo alto de la cascada.
Suponga y = 0 en el fondo para punto de referencia.
¿Altura? Sí (35 m) mgho
¿Resorte? No ½kxo2
¿Velocidad? Sí (vo) ½mvo2

19. Ejemplo 3 (Cont.) El agua en el fondo de la cascad
tiene una velocidad de 30 m/s después de caer 35
¿Cuál es la rapidez del agua
en lo alto de la cascada?
ho = 35 m; vf = 30 m/s2
Luego elija el punto FINAL en el fondo de la
cascada:
¿Altura? No (0 m) mghf
¿Resorte? No ½kxf2
¿Velocidad? Sí (vf) ½mvf2

20. Ejemplo 3 (Cont.) El agua en el fondo de la cascad
tiene una velocidad de 30 m/s después de caer 35
ho = 35 m; vf = 30 m/s2
¿Cuál es la rapidez del
agua en lo alto de la
cascada?
Energía total arriba = Energía total abajo
1 2 1 2 2 2
mgh 2 mv0 0 2 mv f 2gh v 0 v f
2
v0 v2
f 2gh (25.8 m/s)2 2(9.8 m/s2 )(33.2 m)
v0 2
14.9 m /s 2 vo = 3.86 m/s

21. Ejemplo 4. Una bicicleta con velocidad inicial 10
m/s sube hasta una altura neta de 4 m. ¿Cuál es
la velocidad en lo alto, si desprecia la fricción?
vf = ? E(arriba) = E(abajo)
vo = 10 m/s Earriba = mgh + ½mv2
4m
Eabajo = 0 + ½mvo2
1 2 1 2 1 2 1 2
2 mv f mgh 2 mv 0 2 v f 2 v
0 gh
2 2 2 2
v f v 0 2gh (10 m/s) 2(9.8 m/s )(4 m)
vf 21.6 m2 /s2 vf = 4.65 m/s

22. Ejemplo 5: ¿Cuánto subirá, sobre el plano
inclinado de 30o, el bloque de 2 kg después de
liberarse? La constante de resorte es 2000 N/m y
se comprime 8 cm.
Fin
mgho mghf Inicio s
½kxo 2 = ½kxf2 30o
h
½mvo2 ½mvf2
Conservación de energía: ½kxo2 = mghf
2
kx0 (2000 N/m)(0.08m) 2
h h = 0.327 m
2mg 2(2 kg)(9.8 m/s 2 )

23. Ejemplo (Cont.): ¿Cuánto subirá, sobre el plan
inclinado de 30o, el bloque de 2 kg después de
liberarse? La constante de resorte es 2000 N/m
y se comprime 8 cm.
Continúa: Fin
Inicio s
h = 0.327 m = 32.7 cm h
30o
h
sen 30o =
s
h 32.7 cm
s= = s = 65.3 cm
sen 30o sen 30o

24. Conservación de energía y
fuerzas no conservativas.
Se deben explicar las
f fuerzas de fricción. La
energía todavía se
conserva, pero no es
reversible.
Conservación de energía mecánica
(U + K)o = (U + K)f + Pérdidas

25. Estrategias para resolución de
problemas
1. Lea el problema; dibuje y etiquete el bosquejo.
2. Determine los puntos de referencia para
energía potencial gravitacional y/o resorte.
3. Seleccione un punto de inicio y un punto final y
plantee tres preguntas en cada punto:
a. ¿Hay altura? U = mgh
b. ¿Hay velocidad? K = ½mv2
c. ¿Hay un resorte? U = ½kx2

26. Resolución de problemas (continuación
4. Aplique la regla para conservación de energía.
mgho mghf Trabajo
contra
½kxo2 = ½kxf2 + fricción:
½mvo2 ½mvf2 fk x
5. Recuerde usar el valor absoluto (+) del
trabajo de fricción. (Pérdida de energía)

27. Ejemplo 6: Una masa m se conecta a una cuerda d
longitud L y se mantiene horizontalmente como se
muestra. ¿Cuál será la velocidad en el punto B? (d
12 m, L = 20 m)
A
1. Dibuje y etiquete.
2. Comience en A y L vc B d
termine en B. r
3. Referencia U = 0.
0
(U + K)o =(U + K)f + pérdida U=0
mgL + 0 = mg(2r) + ½mvc2 (Multiplique por 2, simplifique)
2gL - 4gr = vc2 Luego encuentre r de la figura.

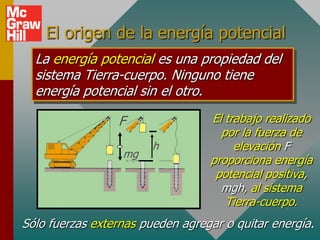
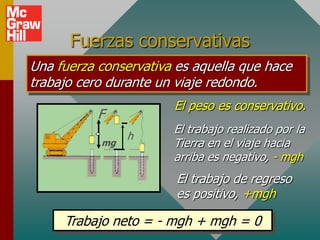
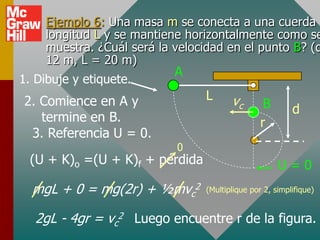
28. Ejemplo (Cont.): Una masa m se conecta a una cuerd
de longitud L y se mantiene horizontalmente como se
muestra. ¿Cuál será la velocidad en el punto B? (d =
m, L = 20 m)
A
2gL - 4gr = vc2
L vc B d
r=L-d
r
r = 20 m - 12 m = 8 m
vc2 =2gL - 4gr = 2g(L - 2r) U=0
vc2 = 2(9.8 m/s2)[20 m - (2)(8 m)]
vc = 2(9.8 m/s2)(4 m) vc = 8.85 m/s

29. Ejemplo 7: Una masa m de 2 kg ubicada 10 m
sobre el suelo comprime un resorte 6 cm. La
constante de resorte es 40,000 N/m y k = 0.4.
¿Cuál es la rapidez cuando llega al fondo?
2 kg
Inicio f n
s mg cos 30o mg sen 30o
h 30o
30o Fin mg
Conservación: mgh + ½kx2 = ½mv2 + fkx
(trabajo)f = ( kn) x = (mg cos 30o) x
continúa . . .

30. Ejemplo (Cont.): Una masa m de 2 kg ubicada
10 m sobre el suelo comprime un resorte 6 cm
La constante del resorte es 40,000 N/m y k =
0.4. ¿Cuál es la rapidez cuando llega al fondo?
2 kg mgh + ½kx2 = ½mv2 + fkx
10 m
x x= = 20 m
h 10 m
sin 30o
30o fkx = (mg cos 30o) x
fkx = (0.4)(2 kg)(9.8 m/s2)(0.866)(20 m) = 136 J
mgh = (2 kg)(9.8 m/s2)(10 m) = 196 J
½kx2 = ½(40,000 N/m)(0.06 m)2 = 72.0 J

31. Ejemplo (Cont.): Una masa m de 2 kg ubicada
10 m sobre el suelo comprime un resorte 6 cm
La constante de resorte es 40,000 N/m y k =
0.4. ¿Cuál es la rapidez cuando llega al fondo?
2 kg mgh + ½kx2 = ½mv2 + fkx
x mgh = 196 J ½kx2 = 72.0 J
h 10 m
30o fkx = 136 J
½mv2 = mgh + ½kx2 - fkx
½(2 kg) v2 = 196 J + 72 J - 136 J = 132 J
v =11.4 m/s

32. Resumen:
Ganancias o pérdidas de energía
Energía potencial gravitacional U = mgh
1 2
Energía potencial de resorte U 2 kx
Energía cinética K 1
mv 2
2
Fricción contra trabajo Trabajo = fx

33. Resumen:
Conservación de energía
Regla básica para conservación de energía:
mgho mghf Trabajo
contra
½kxo2 = ½kxf2 + fricción:
½mvo2 ½mvf2 fk x
Recuerde usar el valor absoluto (+) del
trabajo de fricción. (Pérdida de energía)

34. CONCLUSIÓN:
Conservación de energía