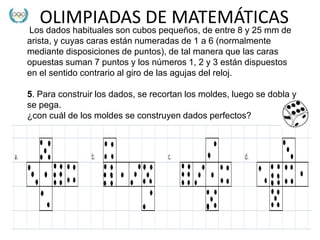
Este documento contiene 15 preguntas de matemáticas sobre varios temas como depreciación de activos, áreas de figuras geométricas, construcción de dados, velocidad en una carrera ciclística, y números reales. Las preguntas requieren calcular porcentajes, expresar áreas y capacidades con fórmulas matemáticas, identificar la relación entre velocidad y tiempo, y clasificar números en la recta numérica.

1. OLIMPIADAS 2012
COLEGIO SANTA ISABEL DE HUNGRIA
ALFONSO LOPEZ.
UNDECIMO

2. OLIMPIADAS DE MATEMÁTICAS
Tenga en cuenta la siguiente información para
responder las preguntas 1a 2.
En una Empresa se compra un articulo que tiene
una vida útil de 10 años en $20.000.000 y se sabe
que la depreciación es directamente proporcional al
tiempo transcurrido desde el momento de la
compra, y cada año se deprecia $1.800.000
1.La depreciación anual del articulo corresponde al
a) 9 % b) 10 % c) 18 % d) 20 %

3. OLIMPIADAS DE MATEMÁTICAS
2. El precio P del articulo al cabo de t años entre 0 y 10
años, está representado por la expresión
a) P (t) = 1.800.000 t – 20.000.000
b) P (t) = 1.800.000 t + 20.000.000
c) P (t) = -1.800.000 t – 20.000.000
d) P (t) = - 1.800.000 t + 20.000.000

4. OLIMPIADAS DE MATEMÁTICAS
La Piscina de el balneario “las Palmas” tiene la forma
rectangular que nos muestra la figura, de 18 metros de
largo por 8 metros de ancho rodeada por una pasarela de
ancho uniforme X (área sombreada)
X
18 m
X
X 18 8m X
X
3.La superficie d la pasarela que es la parte que bordea la
piscina se puede expresar como
a) X [ (36 + 4x) + (16 + 4x)] b) [(18 + 2x) (8 + 2x)]- (18 x 8)
c) (18 + x) (8 + x) d) [(18 + 2x) . X + 8X] – (18 x 8 )

5. OLIMPIADAS DE MATEMÁTICAS
4. La mitad de la piscina es asignada a los niños y tiene
80 cm de profundidad, 2/4 de la mitad se asignan a los
adultos y tiene una profundidad de 1,2 metros, los dos
octavos de la totalidad asignada a los adultos tiene una
profundidad de 1,5 metros y el resto de la asignada a
los adultos, la profundidad es 1,8 metros. ¿Qué parte
del área total de la piscina tiene la máxima
profundidad?
a) 8 metros cuadrados b) 12 metros cuadrados
c) 15 metros cuadrados d) 18 metros cuadrados

6. OLIMPIADAS DE MATEMÁTICAS
Los dados habituales son cubos pequeños, de entre 8 y 25 mm de
arista, y cuyas caras están numeradas de 1 a 6 (normalmente
mediante disposiciones de puntos), de tal manera que las caras
opuestas suman 7 puntos y los números 1, 2 y 3 están dispuestos
en el sentido contrario al giro de las agujas del reloj.
5. Para construir los dados, se recortan los moldes, luego se dobla y
se pega.
¿con cuál de los moldes se construyen dados perfectos?

7. OLIMPIADAS DE MATEMATICAS
6.Un taxi que parte del centro hacia
la iglesia San Mateo, a velocidad
constante, no puede continuar por
la avenida central y debe desviar
por una de las vías alternas. Para
gastar menos gasolina, el taxista
debe
A. desviar por la avenida L, porque el
ángulo ß es mayor que el ángulo α
B. elegir cualquiera de los desvíos,
porque las zonas verdes son de igual
área
C. desviar por la avenida S, porque
recorrerá una distancia menor
D. desviar por la avenida L, porque la
zona verde L es de menor área que la
zona verde S

8. OLIMPIADAS DE MATEMÁTICAS
7. La alcaldía decide tomar una parte de la
zona L para hacer un parqueadero sin que se
altere la forma triangular inicial, éste
quedará ubicado en la esquina de
intersección de la avenida L y la avenida M y
el lado que da a la zona verde debe medir 10
metros. De la zona, el ingeniero afirma que
A. la nueva zona tiene que tener medidas
iguales para conservar la forma
triangular
B. las medidas de la zona de parqueo no se
pueden saber, pues los datos suministrados
en el plano no son suficientes
C. la zona de parqueo ocupará la cuarta
parte de la zona verde L
D. el costado de la zona de parqueo que da a
la avenida L debe medir 30 metros

9. OLIMPIADAS DE MATEMÁTICAS
Para empacar artículos, una empresa
construye cajas de forma cúbica, de
cartón, con tapa y de arista, usando el
siguiente diseño.
8. La expresión que permite determinar la
mínima cantidad de material requerido
para la construcción de cada caja es

10. OLIMPIADA DE MATEMÁTICAS
9. Para empacar dos artículos en una misma
caja la empresa requiere dividirla en dos
compartimientos iguales con una lámina de
cartón, como se indica en la siguiente
figura.
El área de la lámina divisoria, en unidades
cuadradas, está representada por la
expresión

11. OLIMPIADA DE MATEMÁTICAS
10.Para empacar otros artículos la
empresa decide diseñar cajas cúbicas
cuya arista sea el doble de la arista de la
caja original. La capacidad de la nueva
caja es
A. dos veces mayor que la capacidad de la
caja original.
B. cuatro veces mayor que la capacidad de la
caja original.
C. seis veces mayor que la capacidad de la
caja original.
D. ocho veces mayor que la capacidad de la
caja original.

12. CARRERA DE CICLISMO
La gráfica muestra la velocidad alcanzada por Carlos, Rafael y David durante
una carrera de ciclismo.
11.La relación entre la velocidad (v) alcanzada por David y el
tiempo t empleado para recorrerla está representada por la
ecuación
a) b) c) d)

13. 12.

14. OLIMPIADA DE MATEMÁTICAS
13.

15. OLIMPIADA DE MATEMÁTICAS
. en la recta numérica que se muestra, se han ubicado algunos números
reales
El número real
14. Está en el intervalo
a) (-1, 0) y es un número irracional.
b) (-1, 0) y es un número racional.
c) (-4, -3) y es un número irracional.
d) (-4, -3) y es un número racional.

16. 15.