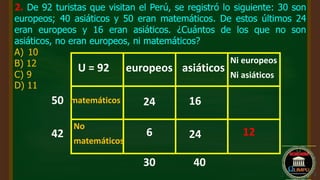
El documento presenta una serie de problemas matemáticos que involucran combinaciones, divisores, promedios y tasas de interés, entre otros. Cada problema es descrito brevemente, seguido de su resolución y cálculos pertinentes. Se abordan temas como conjuntos, divisibilidad, y relaciones de edad, ofreciendo soluciones numéricas específicas.

1. SEMINARIO UNCP 2024

2. 1. Sean los conjuntos A, B y C, que cumplen lo siguiente:
• n(C) = n(A) + n(B)
• n[P(A)] × n[P(B)] × n[P(C)] = 1024
Calcule el número de subconjuntos propios que tiene el
conjunto C.
𝟐𝒏(𝑨)
𝒙 𝟐𝒏(𝑩)
𝒙 𝟐𝒏 𝑨 +𝒏(𝑩)
= 𝟏𝟎𝟐𝟒
𝟐𝟐𝒏 𝑨 +𝟐𝒏(𝑩) = 𝟏𝟎𝟐𝟒
𝟐𝒏 𝑨 +𝒏(𝑩)
= 𝟑𝟐
n(A) + n(B) = 𝟓
n(C) = 𝟓
𝟐𝟓
− 𝟏 = 𝟑𝟏

3. 2. De 92 turistas que visitan el Perú, se registró lo siguiente: 30 son
europeos; 40 asiáticos y 50 eran matemáticos. De estos últimos 24
eran europeos y 16 eran asiáticos. ¿Cuántos de los que no son
asiáticos, no eran europeos, ni matemáticos?
A) 10
B) 12
C) 9
D) 11
europeos asiáticos
Ni europeos
Ni asiáticos
matemáticos
No
matemáticos
U = 92
30 40
50 24 16
6 24
42 12

4. 3. Si 𝟑𝒂𝟏𝒃 +𝟒𝟓𝒂 + 𝟐𝟐𝒃𝒄 + 𝟏𝟎𝒄𝒅 = 𝒆𝟓𝒅
Calcula el valor de 𝒂 + 𝒆.
5 < 𝒂 < 𝒃 < 𝒄 < 𝒅 < 𝟏𝟎
6 7 8 9
𝟑𝟔𝟏𝟕 + 𝟒𝟓𝟔 + 𝟐𝟐𝟕𝟖 + 𝟏𝟎𝟖𝟗 = 𝒆𝟓𝟗
190 + 29 + 151 + 89 = 𝒆𝟓𝟗
e = 4
𝒂 + 𝒆 = 10

5. 4. Si 𝒙𝒙𝒙𝟏𝟒 = 𝒏𝟐 𝒏𝟏𝟎𝒙, determine la diferencia positiva
entre x y n. 𝒙𝒙𝒙𝟏𝟒 = 𝒏𝟐 𝒏𝟏𝟎𝒙
196x + 14x + x = 𝒏𝟐
𝒙𝟑
+n𝒙𝟐
+x
210x = 𝒏𝟐
𝒙𝟑
+ n𝒙𝟐
210 = 𝒏𝟐
𝒙𝟐
+ n𝒙
210 = n𝒙( n𝒙 + 𝟏)
nx = 14
1 14
2 7
7 – 2 = 5
𝒏𝟐
< x < 14

6. 5. Si el CA (𝒂𝒃) = 2 𝒂𝒃 - 20, determinar el CA de
(𝒂 + 𝒃)𝟐
CA (𝒂𝒃) = 2 𝒂𝒃 - 20
100 - 𝒂𝒃 = 2 𝒂𝒃 - 20
120 = 3 𝒂𝒃
40 = 𝒂𝒃 𝒂 = 4 ; b = 0
CA (𝟒 + 𝟎)𝟐
= CA (16) = 100 - 16 = 84

7. 6. Hallar un número de 5 cifras, que multiplicado por 4
da por resultado un número formado por las mismas 5
cifras pero dispuestas en orden invertido. Dar como
respuesta la suma de sus cifras.
Sea un número de cinco cifras 𝒂𝒃𝒄𝒅𝒆
x
4
𝑎𝑏𝑐𝑑𝑒
𝑒𝑑𝑐𝑏𝑎
2
2 8
8 1
1 7
79
9 2 + 1 + 9 + 7 + 8 = 27

8. 7. Calcule el resto que se obtiene al dividir E entre 7, si:
E = 2! + 3! + 4! + ... + 2018! + 2019!
E = 2 + 6 +24 + 120 + 720 + 7 +
o
7 +
o
7 +
o
…
E = 872 + 7
o
E = 7 +
o
4 + 7
o
E = 7 +
o
4
Resto 4

9. 8. Si A = 𝟏𝟐𝟑𝟒𝟓𝟔𝟕𝟖𝟗𝟏𝟐𝟑𝟒 …
𝟑𝟓𝟏 𝒄𝒊𝒇𝒓𝒂𝒔
Calcule el residuo de dividir A entre 11.
123456789
…123456789
+ +
- -
+ +
- -
+ +
- -
+ +
- -
+
-
123456789
+ +
- -
+ +
- -
+
1 – 2 + 3 – 4 + 5 – 6 + 7 – 8 + 9 = 5
11 + 5
o

10. 9. Hallar la cantidad de divisores no primos que
tiene el número: 𝒂 − 𝟒 𝒂(𝒂 − 𝟏)(𝟓 − 𝒂)(𝟓 − 𝒂)𝟔
0 < 𝒂 - 4 4 < 𝒂 5 - 𝒂 ≥ 0 5 ≥ 𝒂
𝒂 = 5
𝟏𝟓𝟒𝟎𝟎𝟔 = 1 x 𝟔𝟒
+ 5 x 𝟔𝟑 + 4 x 𝟔𝟐
𝟏𝟓𝟒𝟎𝟎𝟔 = 2520 = 𝟐𝟑 x 𝟑𝟐
x 𝟓𝟏
x 𝟕𝟏
𝑪𝒅𝒊𝒗 = (3 + 1) (2 + 1)(1 + 1) (1 + 1) = 48
𝑫𝒑𝒓𝒊𝒎𝒐𝒔 = 4
𝑫𝒏𝒐 𝒑𝒓𝒊𝒎𝒐𝒔 = 48 - 4 = 44

11. 10. El número N = 𝟐𝒂
. 𝟓𝟑
tiene 3 divisores
positivos menos que M = 𝟑𝒃
. 𝟓𝒂
, halle la
diferencia positiva de estos números.
𝑪𝒅𝒊𝒗(N) = (𝒂 + 1)4 𝑪𝒅𝒊𝒗(M) =(b + 1)(𝒂 + 1)
(b + 1)(𝒂 + 1) - 3 = (𝒂 + 1)4
(b + 1 – 4 )(𝒂 + 1) = 3
(b – 3 )(𝒂 + 1) = 3
𝟏
ถ
𝟑
b = 4; 𝒂 = 2
N = 500
M = 2025
M - N = 1525

12. 11. Las edades de dos hermanos suman 84 años, si el
máximo común divisor de tales edades es 12. ¿Cuántos años
tiene el mayor si ninguno de ellos tiene más de 50 años?
Sean las edades: P y R
P + R = 84 MCD(P ; R) = 12
MCD(12p ; 12r) = 12
MCD(p ; r) = 1
12p + 12r = 84
p + r = 7
12p ≤ 50 12r ≤ 50
p ≤ 4,∆ r ≤ 4,∆
4 3
12p = 48 ; 12r = 36

13. 12. Javier le dice a Sergio: el MCM de nuestras edades
es el doble de mi edad y el MCD de nuestras edades es
la tercera parte de mi edad. Si yo nací 24 años antes
que tú, ¿cuál es mi edad?
MCM(J; S) = 2J MCD(J; S) =
𝑱
𝟑
MCM(J; S) x MCD(J; S) = JS
2J x
𝑱
𝟑
= JS
2
𝑱
𝟑
= S
𝑱
𝑺
=
𝟑
𝟐
J = 3k S = 2k
3k – 2k = 24
k = 24
J = 3(24) = 72

14. 12. ¿Cuántas fracciones equivalentes a 44/72 tienen
como denominador a un número de tres cifras que
no es múltiplo de 5?
A) 35
B) 40
C) 45
D) 50
E) 55
𝟒𝟒
𝟕𝟐 =
𝟏𝟏
𝟏𝟖
=
𝟏𝟏𝒌
𝟏𝟖𝒌
100 ≤ 18k ≤ 999
5, ∆ ≤ k ≤ 55, ∆
k = 6; 7; 8; …; 55
𝟓𝟎 𝒗𝒂𝒍𝒐𝒓𝒆𝒔
k ≠ 5
o
k ≠ 10; 15; 20;…; 55
𝟏𝟎 𝒗𝒂𝒍𝒐𝒓𝒆𝒔
50 – 10 = 40

15. 14. Sean 𝒂 𝒚 𝒃 enteros positivos tal que:
𝒂
𝟗
+
𝒃
𝟏𝟏
= 1,1919… Calcular el valor de 𝒂 + 𝒃.
𝒂
𝟗
+
𝒃
𝟏𝟏
= 1,෢
𝟏𝟗
𝟏𝟏𝒂+𝟗𝒃
𝟗𝟗
=
𝟏𝟏𝟗−𝟏
𝟗𝟗
𝟏𝟏𝒂 + 𝟗𝒃 = 𝟏𝟏𝟖
7
5
𝑎 + 𝑏 = 12

16. 15. Se tienen 2 números que están en la relación
de 5 a 3. Si la suma de la razón aritmética y
geométrica de dichos números es
𝟒𝟕
𝟑
, calcule la
suma de cifras del mayor
A = 5k B = 3k
5k – 3k + 𝟓
𝟑
=
𝟒𝟕
𝟑
2k =
𝟒𝟐
𝟑
2k = 14
k = 7
A = 5(7) = 35
3 + 5 = 8

17. 16. Con las edades de cuatro amigas se forma una proporción
geométrica. Si los términos medios se diferencian en 8, los
términos extremos en 1 y la suma de todas las edades es 63
años, determine la suma de las edades de las dos menores.
𝒄𝟐
− 𝟓𝟓𝒄 + 756 =
𝟐𝟖−𝒄
𝒄+𝟖
=
𝒄
𝟐𝟕−𝒄
𝒄𝟐
+ 𝟖𝒄
𝟔𝟑𝒄 = 756
𝒄 = 12
𝟏𝟔
𝟐𝟎
=
𝟏𝟐
𝟏𝟓
12 + 15 = 27

18. 17. Se sabe que cierto número de obreros pueden hacer
una obra en 5 días, pero si se contara con 3 obreros más
se podría hacer en solo 2 días. ¿Cuántos obreros serán
necesarios para hacer la obra en un solo día?
Personas Días
36 15
30 (15 + x)
- +
36(15) = 30(15 + x)
36 = 2(15 + x)
18 = 15 + x
x = 3

19. 18. Los engranajes A, B, C y D tienen 20; 60; 30 y 24 dientes
respectivamente. A y B están engranadas, B y C sujetas al mismo
eje, C y D engranadas. Si A da 30 vueltas por minuto, ¿en cuántos
minutos D dará 200 vueltas?
A
20
B
60
C
30
D
24
20(30) = 60𝑽𝑩
10 = 𝑽𝑩 10 = 𝑽𝑪
30(10) = 2𝟒𝑽𝑫
12,5 = 𝑽𝑫
𝟐𝟎𝟎
𝟏𝟐,𝟓
= 16

20. 19. El promedio armónico de 40 números es 16 y el promedio
armónico de otros 30 números diferentes entre sí es 12. Calcule
el promedio armónico de los 70 números.
MH(𝒂𝟏; 𝒂𝟐; 𝒂𝟑 ;…; 𝒂𝟒𝟎) = 16 MH(𝒃𝟏; 𝒃𝟐; 𝒃𝟑 ;…; 𝒃𝟑𝟎) = 12
𝟏
𝒂𝟏
+
40
𝟏
𝒂𝟐
+
𝟏
𝒂𝟑
+…+
𝟏
𝒂𝟒𝟎
= 16 𝟏
𝒃𝟏
+
30
𝟏
𝒃𝟐
+
𝟏
𝒃𝟑
+…+
𝟏
𝒃𝟑𝟎
= 12
𝟏
𝒂𝟏
+
𝟏
𝒂𝟐
+
𝟏
𝒂𝟑
+…+
𝟏
𝒂𝟒𝟎
=
𝟓
𝟐
𝟏
𝒃𝟏
+
𝟏
𝒃𝟐
+
𝟏
𝒃𝟑
+…+
𝟏
𝒃𝟑𝟎
=
𝟓
𝟐

21. 19. El promedio armónico de 40 números es 16 y el promedio
armónico de otros 30 números diferentes entre sí es 12. Calcule
el promedio armónico de los 70 números.
MH(𝒂𝟏; 𝒂𝟐; 𝒂𝟑 ;…; 𝒂𝟒𝟎 ;𝒃𝟏; 𝒃𝟐; 𝒃𝟑 ;…; 𝒃𝟑𝟎) =
70
𝟏
𝒂𝟏
+
𝟏
𝒂𝟐
+
𝟏
𝒂𝟑
+…+
𝟏
𝒂𝟒𝟎
𝟏
𝒃𝟏
+
𝟏
𝒃𝟐
+
𝟏
𝒃𝟑
+…+
𝟏
𝒃𝟑𝟎

22. 20. La media aritmética de tres números enteros positivos es 14, la
media geométrica es igual a uno de ellos y su media armónica es
igual a 72/7. Halle la suma de cifras del mayor de los números.
MA(𝒂; b; c) = 14
𝒂+𝒃+𝒄
𝟑
= 14
𝒂 + 𝒃 + 𝒄 = 42
MG(𝒂; 𝒃; 𝒄; ) = b
𝟑
𝒂𝒃𝒄 = 𝒃
𝒂𝒃𝒄 = 𝒃𝟑
𝒂𝒄 = 𝒃𝟐
MH(𝒂; 𝒃; 𝒄; ) =
𝟕𝟐
𝟕
𝟑𝒂𝒃𝒄
𝒂𝒃+𝒂𝒄+𝒃𝒄
=
𝟕𝟐
𝟕
𝟑𝒃𝟐𝒃
𝒂𝒃+𝒃𝟐+𝒃𝒄
=
𝟕𝟐
𝟕
𝟑𝒃𝟐
𝒂+𝒃+𝒄
=
𝟕𝟐
𝟕
𝟑𝒃𝟐
𝟒𝟐
=
𝟕𝟐
𝟕 𝒃 = 12
𝒂 + 𝒄 = 30 𝒂𝒄 = 144
𝟐𝟒(𝟔)
𝟐 + 𝟒 = 6

23. 21. Se mezclan en un recipiente 80 litros de alcohol de
36°, con 20 litros de alcohol de 56°, si al recipiente se le
extraen “n” litros de mezcla y se reemplaza por la misma
cantidad de agua resultando una mezcla de 28°, halla el
valor de “n”.
VOLÚMENES 80 L 20 L
GRADOS 36° 56°
𝑮𝒎 =
)
𝟖𝟎 𝟑𝟔 + 𝟐𝟎(𝟓𝟔
𝟖𝟎 + 𝟐𝟎
= 40°
VOLÚMENES (100 – n) L n L
GRADOS 40° 0°
𝑮𝒎 =
)
𝟒𝟎(𝟏𝟎𝟎 − 𝐧 + 𝒏(𝟎)
𝟏𝟎𝟎 − 𝒏 + 𝒏
= 28° n= 30

24. 22. Un banco prestó un capital por cinco años a una empresa
ganadera y el monto obtenido fue de S/ 45 000, pero si el tiempo
hubiese sido de siete años, se ganaría S/ 12 000 más. Halle la
tasa de interés trimestral.
Sea el capital: C
Sea el interés anual: I C + 5I = 45 000
C + 7I = 57 000
2I = 12 000
I = 6 000
C = 15 000
I = 6 000
Tasa = r% trimestral
Tiempo = 4 trimestres
6000 =
15000r 4
100
r% = 10%

25. 23. Felipe deposita los 4/7 de su capital en una caja rural con
una tasa del 3% trimestral y el resto al 5% semestral. Si después
de 10 años el interés total fue $ 1170, ¿cuánto fue su capital
inicial?