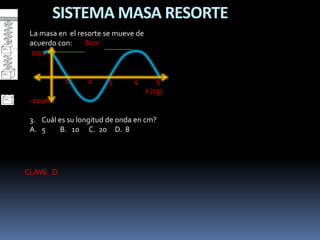
Este documento trata sobre los conceptos básicos de los movimientos armónicos y ondulatorios. Explica que el periodo es el tiempo que tarda una oscilación completa, mientras que la frecuencia es el número de oscilaciones por unidad de tiempo. Luego, analiza cómo cambia el periodo de oscilación de un péndulo o un sistema masa-resorte cuando se modifica su longitud o masa, respectivamente. Finalmente, presenta algunos ejemplos numéricos sobre ondas y movimientos armónicos.

1. EVENTOS ONDULATORIOS
LUIS ANIBAL PANTOJA LÓPEZ

2. MOVIMIENTO ARMÓNICO SIMPLE
PERIODO (T): es el tiempo
empleado en una oscilación.
También:
FRECUENCIA (f): se refiere al
número de oscilaciones dadas por
unidad de tiempo. También :
Como puedes ver el inverso del
periodo es igual a la frecuencia,
es decir:
T: periodo
L: longitud del péndulo,
g: gravedad
OSCILACIÓN: se refiere al movimiento
donde recorre todos los puntos de su
trayectoria o al movimiento de ida y
vuelta
T =
Tiempo empleado
Número de oscilaciones
f =
Número de oscilaciones
Tiempo empleado
f = expresión de gran utilidad
1
T

3. PÉNDULO Y LONGITUD
PREGUNTA: Longitud Periodo RESPUESTA
Si la longitud de un péndulo es L L T Su periodo es T
¿Qué pasa a el periodo T si la
longitud L la alargo cuatro veces?
4L 2T
Su periodo T se duplica , pues raíz
de cuatro es dos
¿Qué pasa al periodo T de un
péndulo de longitud L si su longitud
la reduzco a la cuarta parte?
L/4 T/2
Su periodo T se reduce a la mitad,
pues raíz de ¼ es 1/2
¿Qué pasa al periodo T de un
péndulo si su longitud la hago
nueve veces mayor?
El periodo se triplica
L/9
5T
16L
T = 2π L
g
-X
X = 0
Ec = max
Ep = 0
X
Ec = 0
Ep = max

4. PÉNDULO Y LONGITUD
PREGUNTA: Longitud Periodo RESPUESTA
Si la longitud de un péndulo es L L T Su periodo es T
¿Qué pasa a el periodo T si la
longitud L la alargo cuatro veces?
4L 2T
Su periodo T se duplica , pues raíz
de cuatro es dos
¿Qué pasa al periodo T de un
péndulo de longitud L si su longitud
la reduzco a la cuarta parte?
L/4 T/2
Su periodo T se reduce a la mitad,
pues raíz de ¼ es 1/2
¿Qué pasa al periodo T de un
péndulo si su longitud la hago
nueve veces mayor?
El periodo se triplica
L/9
5T
16L
T = 2π L
g
-X
X = 0
Ec = max
Ep = 0
X
Ec = 0
Ep = max

5. PÉNDULO Y GRAVEDAD
PREGUNTA: Gravedad Periodo RESPUESTA
Si la gravedad g de un planeta donde está un
péndulo de longitud L, cuál es su periodo T?
g T Su periodo es T
¿Qué pasa al periodo T si lo llevo a un planeta
cuya gravedad sea cuatro veces la de la
Tierra?
4g T/2
Su periodo T se reduce a la mitad,
pues raíz de cuatro dos y la inversa
de 2 es 1/2G
¿Qué le pasa al periodo T de un péndulo de
longitud L, si lo llevo a un planeta cuya
gravedad sea la cuarta parte que la de la
Tierra?
g/4 2T
Su periodo T aumenta al doble,
pues raíz de 1/4 es ½ y como la
inversa de ½ es dos, pues el periodo
se duplica.
Qué le pasa al periodo T de un péndulo si lo
llevo a un planeta cuya gravedad sea nueve
veces la de la Tierra?
El periodo se triplica
g/9
5T
T = 2π L
g
-X
X = 0
Ec = max
Ep = 0
X
Ec = 0
Ep = max

6. PÉNDULO Y GRAVEDAD
PREGUNTA: Gravedad Periodo RESPUESTA
Si la gravedad g de un planeta donde está un
péndulo de longitud L, cuál es su periodo T?
g T Su periodo es T
¿Qué pasa al periodo T si lo llevo a un planeta
cuya gravedad sea cuatro veces la de la
Tierra?
4g T/2
Su periodo T se reduce a la mitad,
pues raíz de cuatro dos y la inversa
de 2 es 1/2G
¿Qué le pasa al periodo T de un péndulo de
longitud L, si lo llevo a un planeta cuya
gravedad sea la cuarta parte que la de la
Tierra?
g/4 2T
Su periodo T aumenta al doble,
pues raíz de 1/4 es ½ y como la
inversa de ½ es dos, pues el periodo
se duplica.
Qué le pasa al periodo T de un péndulo si lo
llevo a un planeta cuya gravedad sea nueve
veces la de la Tierra?
El periodo se triplica
g/9
5T
T = 2π L
g
-X
X = 0
Ec = max
Ep = 0
X
Ec = 0
Ep = max

7. SISTEMA MASA RESORTE
Pregunta Masa Periodo Respuesta
Si la masa es m, ¿Cuál es el periodo? m T El periodo es T
Si la masa se cuadruplica, ¿Cuál es su
periodo T?
4m 2T
Su periodo es el doble 2T , pues la raíz
de cuatro es 2
¿Qué le pasa al periodo T si la masa la
reduzco a la cuarta parte?
m/4 T/2
El periodo se reduce a la mitad , ya que
raíz de ¼ es un medio
9m
T/3
T = 2π m
k
ECUACIONES
Y = A sen(wt) Ymax = A
V = A.W Cos(wt) Vmax = A . W
a = -A.W2 Sen(wt) amax = -A . W2
V=0
amax
Vmax
a =0
V=0
amax
m

8. SISTEMA MASA RESORTE
Pregunta Masa Periodo Respuesta
Si la masa es m, ¿Cuál es el periodo? m T El periodo es T
Si la masa se cuadruplica, ¿Cuál es su
periodo T?
4m 2T
Su periodo es el doble 2T , pues la raíz
de cuatro es 2
¿Qué le pasa al periodo T si la masa la
reduzco a la cuarta parte?
m/4 T/2
El periodo se reduce a la mitad , ya que
raíz de ¼ es un medio
9m
T/3
T = 2π m
k
ECUACIONES
Y = A sen(wt) Ymax = A
V = A.W Cos(wt) Vmax = A . W
a = -A.W2 Sen(wt) amax = -A . W2
V=0
amax
Vmax
a =0
V=0
amax
m

9. SISTEMA MASA RESORTE
Pregunta Masa Periodo Respuesta
Si la masa es m, ¿Cuál es el periodo? m T El periodo es T
Si la masa se cuadruplica, ¿Cuál es su
periodo T?
4m 2T
Su periodo es el doble 2T , pues la raíz
de cuatro es 2
¿Qué le pasa al periodo T si la masa la
reduzco a la cuarta parte?
m/4 T/2
El periodo se reduce a la mitad , ya que
raíz de ¼ es un medio
9m
T/3
T = 2π m
k
ECUACIONES
Y = A sen(wt) Ymax = A
V = A.W Cos(wt) Vmax = A . W
a = -A.W2 Sen(wt) amax = -A . W2
V=0
amax
Vmax
a =0
V=0
amax
m

10. GRÁFICAS DEL MAS
EN EL PUNTO
“A”
EN PUNTO DE
EQUILIBRI”O “
EN EL PUNTO
“B”
V =0 V = máxima V = 0
F máxima + F = 0 F máxima -
Acel.max a= 0 Acel. max
V
A O B O A
F
A O B O A
Cada figura seno o coseno corresponde a una oscilación.A B
O

11. GRÁFICAS DEL MAS
EN EL PUNTO
“A”
EN PUNTO DE
EQUILIBRI”O “
EN EL PUNTO
“B”
V =0 V = máxima V = 0
F máxima + F = 0 F máxima -
Acel.max a= 0 Acel. max
V
A O B O A
F
A O B O A
Cada figura seno o coseno corresponde a una
oscilación.
A B
O

12. APLICACIONES
.
Un sismógrafo dibuja en 2 sg la siguiente figura :
4mm
2mm
-2mm
-4mm ____2cm____
1.Cuál es su frecuencia?
A. 3/2 hz. B. 2/3 HZ
C. 2 HZ D. 4HZ
CLAVE A
Recordemos que cada oscilación corresponde a una figura seno o coseno, en la
figura se forman tres figuras seno por tanto dio 3 oscilaciones en dos segundos,
y la frecuencia se define como numero de oscilaciones por tiempo empleado
por ello la frecuencia es : f = 3/2 , da tres oscilaciones en dos segundos

13. APLICACIONES
.
Un sismógrafo dibuja en 2 sg la siguiente figura :
4mm
2mm
-2mm
-4mm ____2cm____
. Cuál es su periodo?
A. 3/2 s B. 2/3 sg
C. 2 sg D. 4 sg
CLAVE B

14. APLICACIONES.
Un sismógrafo dibuja en 2 sg la siguiente figura :
4mm
2mm
-2mm
-4mm ____2cm____
3. Cuál es su velocidad, en cm/s ?
A. 3/2. B. 2
c. 3 D. 4
CLAVE C
cada figura seno o coseno corresponde a una distancia llamada
longitud de onda λ y como bien sabemos el tiempo de cada
oscilación se llama periodo T, y entendiendo el movimiento
ondulatorio como uniforme entonces:
V =
𝒙
𝒕
=
𝛌
𝑻
= λ . f ………. se usó que
1
𝑇
= f
V = λ . f = 2cm . 3/2 hz = 3 cm/s.

15. APLICACIONES.
Un sismógrafo dibuja en 2 sg la siguiente figura :
4mm
2mm
-2mm
-4mm ____2cm___
3. Cuál es su amplitud?
A. 8 mm. B. 6 mm
c. 2 mm D. 4 mm
CLAVE D

16. SISTEMA MASA RESORTE
V λ
- A O A O -A O A
En el
punto A
En punto
de
equilibrio
O
En el
punto -A
Cuando el cuerpo se mueve desde A hasta -A la
velocidad es negativa se desplaza hacia abajo.
En cualquier parte desde o hasta –A el resorte
empuja hacia o es decir hacia arriba , por lo
tanto su fuerza es positiva, por el contrario la
fuerza es negativa en cualquier punto cuando la
masa se encuentre entre O y A
En el
punto A
V = 0
En punto
de
equilibrio
O
V= máx.
En el
punto -A
V = 0
En el
punto A
V = 0
F máx. –
Hacia
abajo
En punto
de
equilibrio
O
V= máx. F = O
En el
punto -A
V = 0
F máx. +
Hacia
arriba
En el
punto A
V = 0
F máx. –
Hacia
abajo
Acel. máx.
En punto
de
equilibrio
O
V= máx. F = O Acel. =0
En el
punto -A
V = 0
F máx. +
Hacia
arriba
Acel. máx.

17. La masa en el resorte se mueve de
acuerdo con: 8cm
10cm
1 2 3 4 5
t (sg)
-10cm
1. Cuál es su periodo en segundos?:
A. 8 B. 3 C.4 D.5
SISTEMA MASA RESORTE
CLAVE C

18. La masa en el resorte se mueve de
acuerdo con: 8cm
10cm
1 2 3 4 5
t (sg)
-10cm
2. Cuál es su amplitud en cm?:
A. 5 B. 10 C.4 D.20
SISTEMA MASA RESORTE
CLAVE B

19. La masa en el resorte se mueve de
acuerdo con: 8cm
10cm
1 2 3 4 5
t (sg)
-10cm
3. Cuál es su longitud de onda en cm?
A. 5 B. 10 C. 20 D. 8
SISTEMA MASA RESORTE
CLAVE D

20. La masa en el resorte se mueve de
acuerdo con: 8cm
10cm
1 2 3 4 5
t (sg)
-10cm
4. La velocidad de la onda es en cm/sg:
A. 2 B. 4 C. 8 D. 5
SISTEMA MASA RESORTE
CLAVE A
cada figura seno o coseno
corresponde a una distancia llamada
longitud de onda λ y como bien
sabemos el tiempo de cada
oscilación se llama periodo T, en la
figura anterior el coseno se da en un
tiempo de T =4sg , su inversa será la
frecuencia f=1/4 y su distancia o
longitud de onda λ =8cm
V =
𝒙
𝒕
=
𝛌
𝑻
= λ . f
V = λ . f
V = 8cm .
𝟏
𝟒
hz
V = 2 cm/s.

21. La masa en el resorte se mueve de
acuerdo con: 8cm
10cm
1 2 3 4 5
t (sg)
-10cm
4. La velocidad es máxima en t :
A. 2 ,4,6 …
B. 1,3,5…
C. 1,3,4,5…8
D. 1,7,10…
SISTEMA MASA RESORTE
CLAVE B
La masa del resorte se comprimió
desplazándola 10 cm hacia arriba y
desde allí se dejo libre empezando
un MAS, en el punto mas alto
donde se soltó su velocidad es cero
y empieza a ganar velocidad hasta el
punto de equilibrio central, desde
allí hasta abajo empieza a frenar
hasta detenerse en el punto inferior
más bajo a -10 cm , luego asciende
ganando velocidad llegando a su
máxima en el punto central, por eso
concluimos que cada vez que pase
por el punto de equilibrio en 1 sg,
3sg, 5 sg su velocidad será máxima.
.

22. FENÓMENOS ONDULATORIOS
REFLEXIÓN: se presenta cuando una
onda cambia de dirección
SOLOMEO
PAREDES

23. FENÓMENOS ONDULATORIOS
2. DIFRACCIÓN: la onda bordea los
obstáculos adecuados
Cesar Noso

24. b. I. CONSTRUCTIVA:
AMPLIFICADORES
SONIDO + SONIDO = SONIDOMAYOR
( NO EL DOBLE)
a . I. DESTRUCTIVA:
SILENCIADORES
SONIDO + SONIDO = SILENCIO

25. REFRACCIÓN
La frecuencia de las dos ondas sonora y óptica conservan
Refracción refracción
De sonido De luz
V aire=340m/s v aire= 3 . 10 8m/s
V sonido en el
agua=1450 mt/sg
V = λ . F
+ + cte
V de la luz
agua=2,25..10 8 m/s
V = λ . F
+ - cte

26. REFRACCIÓN
se presenta cuando una onda
cambia de medio, mantiene
constante su frecuencia y cambia
su velocidad y longitud de onda λ
DESCOMPOSICION DE LA LUZ
COMPOSICIÓN DE LA LUZ
LONGITUD
DE ONDA
-3
-2
-1
1
2
3
Si en un disco de Newton se
pintan tres colores, dos de ellos
son el violeta y el amarillo el
tercer color para que al girar se
vea blanco es?:
a. Rojo b. naranja
c. verde d. azul
Si este disco de Newton se
pone a girar se observa de
color o luz blanca.
La luz se integra : -6 + 6 = 0
CLAVE B
Violeta + amarillo + ? = blanca
3 - 1 + ? = 0
3 - 1 - 2 = 0
La frecuencia ASOCIADA para que
la suma de cero corresponde a -2 ,
es decir color naranja.
FRECUENCIA
asociada

27. En una carretera fututurista se deben
respetar los semáforos, pero los autos o
motos pueden viajar sin limites de
velocidad.
Un motosiclista acercarse a gran velocidad
hacia un semáforo que esta en luz roja
se lo pasa y el motociclista y el policía
de transito argumentan:
I: motociclista: por efecto Doppler al
acercarme la luz la vi verde
II . Policía. El efecto Doppler en los colores
se presenta si la moto se acerca a
velocidad comparable con la de la luz
por eso la vio roja.
a. Los dos tienen razón
b. Solo el motociclista tiene razón
c. Solo el policía tiene razón
d. Ninguno tiene razón

28. VELOCIDAD DE LA ONDA EN UNA CUERDA
Las ondas transversales se presentan
en las cuerdas y su velocidad de
propagación depende de la tensión
de la cuerda T y de la densidad de
la cuerda µ o masa por unidad de
longitud que tenga la cuerda, es
decir µ = m/L
T = tensión
µ = densidad de la cuerda
µ = m/L
m = masa
L = longitud de la cuerda
Con estos elementos la velocidad de la
cuerda se calcula con:
V = T
µ
La velocidad d
es v y…
V T …su tensión es T
La velocidad se
duplica si…
2v
La velocidad d es v
y…
V µ …su densidad es µ
La velocidad se
duplica si…
2v
La velocidad d
es v y…
V T …su tensión es T
La velocidad se
duplica si…
2v 4T ….su tensión se
cuadruplica
La velocidad se
reduce a la
mitad si…
v/2 T/4 La tensión se reduce a
la cuarta parte
3v
T/3
La velocidad d
es v y…
V T …su tensión es T
La velocidad se
duplica si…
2v 4T ….su tensión se
cuadruplica
La velocidad d
es v y…
V T …su tensión es T
La velocidad se
duplica si…
2v 4T ….su tensión se
cuadruplica
La velocidad se
reduce a la
mitad si…
v/2
La velocidad d
es v y…
V T …su tensión es T
La velocidad se
duplica si…
2v 4T ….su tensión se
cuadruplica
La velocidad se
reduce a la
mitad si…
v/2 T/4 La tensión se reduce a
la cuarta parte
3v
T/3
La velocidad d es v
y…
V µ …su densidad es µ
La velocidad se
duplica si…
2v µ/4 ….su densidad se
reduce a la cuarta
parte
La velocidad se
reduce a la mitad
si…
v/2
3v
La velocidad d es v
y…
V µ …su densidad es µ
La velocidad se
duplica si…
2v µ/4 ….su densidad se
reduce a la cuarta
parte
La velocidad se
reduce a la mitad
si…
v/2 4µ La densidad se
cuadruplica
3v
µ /3

29. APLICACIÓN
En una cuerda de guitarra se
pulsa y vibra con
frecuencia “f”, para que al
pulsar otra cuerda del
doble de masa vibre con
la misma frecuencia es
necesario que la cuerda.
a. La tensión T se reduzca a
la mitad
b. La tensiónT se duplique
c. La tensión T se
mantenga
d. Se cuadruplique la
tensión
Las ondas transversales se
presentan en las cuerdas y su
velocidad de propagación
depende de la tensión de la
cuerda T y de la densidad de la
cuerda µ o masa por unidad de
longitud que tenga la cuerda, es
decir
µ = m/L
Con estos elementos la velocidad
de la cuerda se calcula con:
V = T
µ
V = 2 T
2 µ
CLAVE B

30. CUERDAS Y TUBOS SONOROS
CUERDA L? λ? V = λ .F F?
TUBO ABIERTO L ?-Para cuerdas y tubos abiertos la formula
general: F = n v
2L
Donde n es el armónico deseado:1,2,3..
-Para tubos abiertos la ecuación general es :
F=n v
2L
Para tubos observa que L y F tienen la misma
fracción, entonces sólo hay que averiguar que
parte de sen o cos se forma
λ? V = λ .F F?
2L= λ
2L = λ
2
2L = λ
3
λ? V = λ .F F?
2L= λ V=2L.F 1V =F
2L
2L = λ
2
V=2L.F
2
2V =F
2L
2L = λ
3
V=2L.F
3
3V =F
2L
TUBO CERRADO L? F?
V =F
4L
3V =F
4L
5V =F
4L
F?
V =F
2L
2V =F
2L
3V =F
2L
L =
2λ
𝟐
L =
λ
𝟐
L =
3λ
𝟐
L =
λ
𝟒
L =
3 λ
𝟒
L =
5 λ
𝟒
L =
λ
𝟐
L =
2λ
𝟐
L =
3λ
𝟐

31. APLICACIONES
En cada uno de los tres tubos mostrados están
vibrando con su primer armónico, el tubo III es
abierto:
L
I
2L
II
3L
III
3. La relación FI / FII es:
a. 1 b. 2 c.3 d.4
4. velocidad de la onda en cada tubo es:
A. VI =VII=VIII b. VI <VII <VIII
c. VI >VII>VIII d . VI = 2VII=3VIII
5. Una cuerda de guitarra vibra con una frecuencia f
para una segunda cuerda de el doble de masa
vibre con la misma frecuencia :
a. Duplicamos la tensión en la segunda
b. Reducimos a la mitad la tensión
c. Cuadruplicamos la tensión
d. Reducimos a la cuarta parte la tensión
1
2

32. APLICACIONES1
CLAVE c

33. APLICACIONES
2
CLAVE A
3v / 2L
3v / L
v / 2L
v / L

34. APLICACIONES
En cada uno de los tres tunos mostrados están
vibrando con su primer armónico, el tubo
III es abierto:
L
I
2L
II
3L
III
3. La relación FI / FII es:
a. 1 b. 2 c.3 d.4
CLAVE B

35. APLICACIONES
En cada uno de los tres tunos mostrados están
vibrando con su primer armónico, el tubo III es
abierto:
L
I
2L
II
3L
III
1
2
4. velocidad de la onda en
cada tubo es:
A.VI =VII=VIII
B. VI <VII <VIII
c. VI >VII>VIII
D VI = 2VII=3VIII
CLAVE A

36. APLICACIONES
En cada uno de los tres tunos
mostrados están vibrando con su
primer armónico, el tubo III es
abierto:
L
I
2L
II
3L
III
4. Una cuerda de guitarra vibra con una frecuencia f
para una segunda cuerda de el doble de masa
vibre con la misma frecuencia :
a. Duplicamos la tención en la segunda
b. Reducimos a la mitad la tensión
c. Cuadruplicamos la tensión
d. Reducimos a la cuarta parte la tensión
1 CLAVE B

37. EFECTO DOPPLER
pero se simplifican en la siguiente
recomendación para el signo enVo y para la
velocidad de la fuente Vf
- + - +
O f

38. APLICACION
Cuando una fuente sonora se
mueve con velocidad mayor
a la del sonido se genera una
onda de choque en
interferencia constructiva
quien muestra esto es:
Si la fuente sonora es un avión
supersónico y cuando estaba en el
punto O1 produjo una onda ( verde )
que ha viajado una distancia
equivalente a su radio r , el avión a
superado esa distancia r y esta mas
delante del frente de onda inicial.
Cuando el avión paso por O2 el avión
produjo un frente de onda nuevo
(rojo) que a su vez el avión supera en
su velocidad , pero los frentes de
onda (verde y rojo) interfieren en un
momento constructivamente,
produciendo la onda de choque
O1 O2
CLAVE B

39. APLICACION
 1. de acuerdo con el gráfico
mostrado y si tenemos en
cuenta la velocidad de la
onda comoVo.Y la velocidad
de un avión comoVa.
 a.V a =Vo
 b.V a >Vo
 d.V a <Vo
 d.V a = 2Vo
CLAVE A

40. ESPEJOS
ESPEJO PLANO . DE UN PUNTO ,
ANGULAR Y DEL TAMAÑO
NECESARIO DE UN ESPEJO
PARAVERSE POR COMPLETO:
.
h= H /2
El número de imágenes en un espejo angular
es n
N = 360 - θ
θ
cuantas imágenes se obtienen al colocar un
objeto frente aun espejo angular de 90°
A. 3 B. 4 C. 11 D. 6

41. IMAGEN EN UN ESPEJO PLANO
LA IMAGEN ESVIRTUAL , DE IGUALTAMAÑO

42. LA IMAGEN DE UN OBJETO SITUADO ENTRE ∞ Y C
.
.
LA IMAGEN ES REAL, INVERTIDAY DE MENORTAMAÑO

43. IMAGEN DE UN OBJETO SITUADO EN EL CENTRO DE CURVATURA
LA IMAGEN ES REAL, INVERTIDAY DE IGUALTAMAÑO

44. LA IMAGEN ES REAL, INVERTIDA Y DE MAYOR TAMANO
IMAGEN DE UN OBJETO SITUADO ENTRE CY F

46. EN CONCLUSION LA IMAGEN INV. VA CRECIENDO CUANDO SE ACERCA A V:
∞ C F V
INV MENOR IGUAL MAYOR NO HAY DERECHA
TAMAÑO TAMAÑO TAMAÑO IMAGEN MAYOR
REAL REAL REAL REAL VIRTUAL

47. IMAGEN EN UN ESPEJO CONVEXO
IMAGENVIRTUAL, DERECHA Y DE MENORTAMAÑO

48. APLICACION
El objeto mostrado a la izquierda al
colocarse al frente de un espejo da
como resultado la imagen de la
derecha.
a. Cóncavo entre el infinito y c
b. Cóncavo en c
c. Cóncavo entre c y f
d. convexo
CLAVE A

49. APLICACION
El objeto mostrado a la izquierda al
colocarse al frente de un espejo da
como resultado la imagen de la
derecha.
a. Cóncavo entre el infinito y c
b. Cóncavo en c
c. Cóncavo entre c y f
d. convexo
CLAVE D
SOLUCI{ON

50. APLICACION
El objeto mostrado a la izquierda al
colocarse al frente de un espejo da
como resultado la imagen de la
derecha.
a. Cóncavo entre el infinito y c
b. Cóncavo en c
c. Cóncavo entre c y f
d. convexo
SOLUCION:
CLAVE B
Existen tres tipos
existen tres tipos de
personas las que saben
contar y las que no
Existentrestipos
existentrestiposde
personaslasquesaben
contarylasqueno

51. APLICACION
El objeto mostrado a la izquierda al
colocarse al frente de un espejo da
como resultado la imagen de la
derecha.
a. Cóncavo entre el infinito y c
b. Cóncavo en c
c. plano
d. convexo
CLAVE C

52. APLICACION
El objeto mostrado a la izquierda al
colocarse al frente de un espejo da
como resultado la imagen de la
derecha.
a. Cóncavo entre el infinito y c
b. Cóncavo en c
c. Cóncavo entre f y v
d. convexo CLAVE C

53. EL OJO HUMANO
OJO NORMAL
OJO MIOPEY CORRECCIÓN
OJO HIPERMETROPEY CORRECCIÓN
LENTES :
CONVERGENTESO
BICONVEXA
LENTE DIVERGENTEO
BICONCAVA

54. OJO HUMANO
OJO NORMAL

55. MIOPIA Y CORRECCION
MIOPIA  CORRECCION
LENTES DIVERGENTES
OJO NORMAL

56. HIPERMETROPIA CORRECCION
LENTES CONVERGENTE