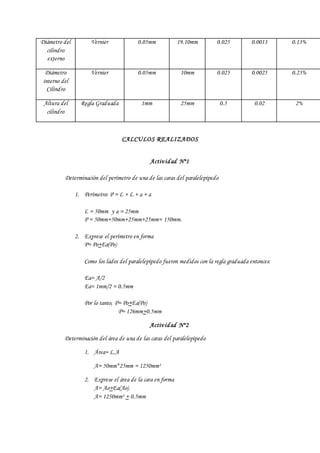
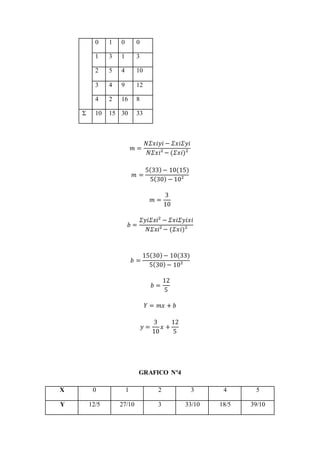
Este documento presenta los resultados de una práctica de laboratorio sobre mediciones físicas y representaciones gráficas. Se midieron varias cantidades como la longitud, diámetro y altura de objetos usando instrumentos como regla graduada, tornillo micrométrico y vernier. Se calculó el error absoluto y relativo de cada medición. Adicionalmente, se graficaron tres conjuntos de datos experimentales y se determinó la ecuación que representa mejor cada relación mediante el cálculo de la pendiente y la ordenada al origen.

1. INTUNIVERSIDAD FERMIN TORO
VICERRECTORADO ACADEMICO
FACULTAD DE INGENIERIA
PRACTICA Nº 2
GRAFICOS
Autor: Alvimar Vargas: 23849955
Seccion: Saia
Cabudare, 2015

2. INTRODUCCIÓN
Al momento en que se realizan medidas directas de magnitudes físicas, todo lo que se
obtiene es importante para el análisis.
Existen cantidades físicas que se encuentran fuera del alcance en el cual los sentidos
humanos no pueden percibir, es necesario el uso de instrumentos de medición que nos permiten
cuantificar los valores.
Los instrumentos que utilizamos enesta práctica fueron:la reglagraduada, eltornillo
micrométrico y el vernier; ellos nos facilitaron el trabajo en el laboratorio al tener q medir los
objetos correspondientes.
OBJETIVOS ESPECÍFICOS
1. Determinar las apreciaciones e interpretar su significado, de una serie de
instrumentos de medida.
2. Estimar el error absoluto cometido al realizar cualquier medición directa.
3. Expresar cualquier medida que se efectúe, bajo la forma:
V= Vo + Ea (Vo).
4. Calcular el error relativo y porcentual de cualquier medida e interpretarla.
5. Operar con cifras significativas.
DATOS EXPERIMENTALES
CANTIDAD
FISICA A
MEDIR
INSTRUMENTO APRECIACION VALOR
OBTENIDO
ERROR
ABSOLUTO
ERROR
RELATIVO
ERROR
PORCENTUAL
Largo del
paralelepípedo
Regla Graduada 1mm 50mm 0.5 0.01 1%
Ancho del
Paralelepípedo
Regla Graduada 1mm 25mm 0.5 0.02 2%
Diámetro de
la Esfera
Tornillo
Micrométrico
0.001mm 19.709mm 0.0005 0.000025 0.0025%
Diámetro
externo del
Cilindro
Tornillo
Micrométrico
0.001mm 15.234mm 0.0005 0.000032 0.0032%

3. CALCULOS REALIZADOS
Actividad Nº1
Determinación del perímetro de una de las caras del paralelepípedo
1. Perímetro: P = L + L + a + a
L = 50mm y a = 25mm
P = 50mm+50mm+25mm+25mm= 150mm.
2. Exprese el perímetro en forma
P= Po+Ea(Po)
Como los lados del paralelepípedo fueron medidos con la regla graduada entonces:
Ea= A/2
Ea= 1mm/2 = 0.5mm
Por lo tanto, P= Po+Ea(Po)
P= 126mm+0.5mm
Actividad Nº2
Determinación del área de una de las caras del paralelepípedo
1. Área= L.A
A= 50mm*25mm = 1250mm²
2. Exprese el área de la cara en forma
A= Ao+Ea(Ao)
A= 1250mm² + 0.5mm
Diámetro del
cilindro
externo
Vernier 0.05mm 19.10mm 0.025 0.0013 0.13%
Diámetro
interno del
Cilindro
Vernier 0.05mm 10mm 0.025 0.0025 0.25%
Altura del
cilindro
Regla Graduada 1mm 25mm 0.5 0.02 2%

4. Actividad Nº3
Determinación del volumen del cilindro recto (macizo)
1. Volumen:
𝑉 =
𝜋𝑟2
4
𝐻
Donde: 𝑟 = 7.617𝑚𝑚
𝐻 = 25𝑚𝑚
Entonces, 𝑉 =
3.14(7.617𝑚𝑚 )²
4
x25mm
oPnotPoo roP
V=1139.19mm²
2. Exprese el volumen de la forma
V= Vo+Ea(Vo)
Como el diámetro fue medido con el vernier y la altura con la regla graduada, entonces:
V= 1139.19 mm+0.025mm
V= 1139.19 mm+0.5mm
CONCLUSIONES Y RECOMENDACIONES
Conclusiones:
Una vez finalizada la práctica se puede concluir que existen diferentes tipos de instrumentos
de medición; entre los cuales podemos mencionar: el vernier, el tornillo micrométrico y la regla
graduada).
Unos son más precisos que otros, por ejemplo, el tornillo micrométrico es más preciso que el
vernier, y a su vez, el vernier es más preciso que la regla graduada. Esto se debe a que el tornillo
micrométrico tiene 3 niveles de escalas, el vernier 2, y lareglagraduada solo tiene 1 nivel de escala, lo
que ayuda a obtener una medida más exacta con un margen de error mucho menor.

5. Lo planteado anteriormente, se puede observar claramente en la tabla realizada en el
laboratorio, allí vemos como el error absoluto de la regla graduadaes mayor que el del vernier, y el del
vernier es mayor que el del tornillo micrométrico.
Por lo tanto elnivelde precisiónde cadainstrumentode mediciónviene dadapor laapreciación
que cada uno de estos posea; el tornillo micrométrico tiene una apreciación de 0.001mm, el vernier de
0.05mm, y la regla graduada de 1mm.
Recomendaciones:
A la hora de medir cualquier objeto, podemos utilizar los instrumentos de medición que
prefiramos; pero una vez analizadas las conclusiones, dependiendo del objeto a medir, podemos
recomendar que se utilicen los instrumentos de medición más precisos para que el margen de error sea
menor.
ANEXOS
Post-laboratorio:
1. ¿Qué significa medir una magnitud física?
Toda medición consiste en atribuir un valor numérico cuantitativo a alguna propiedad de un
cuerpo, como la longitud o el área. Estas propiedades, conocidas bajo el nombre de magnitudes físicas,
pueden cuantificarse por comparación con un patrón o con partes de un patrón. Constituyen ejemplos
de magnitudes físicas: la masa, la longitud, el tiempo, la densidad, la temperatura, la velocidad, la
aceleración, la energía, etc.
2. ¿Cuáles son las cantidades básicas de la física?
Las cantidades físicas, son elementos de construcción de la física, en función de los cuales se
expresan las leyesde lamisma. Por ejemplo:fuerza, tiempo, velocidad, densidad, temperaturay muchas
otras que existen en la Física.
Las cantidades físicas fundamentales, son aquellas que no pueden ser expresadas a partir de
otras, ejemplo: longitud, masa y tiempo; mientas que las cantidades físicas derivadas son las que se
expresan en función de las fundamentales, ejemplo: área volumen, fuerza, velocidad y cantidad.
3. ¿Por qué la medidade precisión realizada con un vernier tiene más precisión que la realizada
con una regla graduada?
Porque el vernier posee 2 niveles de escalas y unaapreciación de 0.05mm, mientras que laregla
graduada posee 1 nivel de escala y una apreciación de 1mm.
4. ¿Cómo podemos medir el tiempo que tarda una pelota en caer desde 10mts de altura?
El instrumento de medición más acorde para tomar dicho tiempo es el cronómetro, ya que la
aplicación del cronómetro es lade un reloj que mide con gran precisión, un tiempo determinado. En este

6. caso se dejarácaer la pelotadesde los10mts y a lavezse pulsaelbotón delcronómetro para que empiece
a tomar el tiempo, cuando la pelota toque el piso se detiene el cronómetro y sabremos cuanto tiempo
tardó.
5. ¿Cómo mediría usted el tiempo que tarda una rueda en dar una vuelta?
Este ejemplo es similar al anterior, también podemos utilizar el cronómetro para tomar el
tiempo que tarda una rueda en dar una vuelta.
6. ¿Usted mediríael espesor de unaláminadelgadacon mayor precisión con: a) un vernier (0.02)
mm b) un calibrador palmer o tornillo micrométrico (0.01) mm c) una regla graduada (0.1) cm?
El espesor de una lámina delgada se mediría con mayor precisión un tornillo micrométrico ya
que su nivel de apreciación es de 0.01mm, mucho menor que el de laregla graduaday el vernier, por lo
tanto es más preciso.
7. Si se hacen dos medidas de unamismalongitud y resulta: L1 = (10.0+ 0.01) cm y L2 = (10.5+
0.19)cm. ¿Cuál de las 2 medidas es más precisa?
La L1 es más precisayaque fue realizadacon uninstrumento de mediciónde menor apreciación
y por ende el error absoluto es menor.
8. Una hoja de papel rectangular tiene las siguientes medidas: L1 = (20.00+0.19cm L2= (32.5+
0.1)cm
Calcule:
 El perímetro de la hoja y expréselo como: P=Po+Ea(Po)
P= L1+L1+L2+L2
P= 10cm+10cm+10.5cm+10.5cm
P= 41cm
 El área de la hoja como: A=Ao+Ea(Ao).
A= L1*L2
A= 10cm*10.5cm
A= 105cm2
9. Los lados de un triángulo isósceles son: L1=L2= (20.0+0.1)cm y L3=(15.0+0.1)cm
H=(18.5+0.1)cm
Calcule:
 Perímetro
P= L1+L2+L3
P= 20cm+20cm+15cm
P= 55cm
 Área
𝐴 =
𝑏. ℎ
2
Considerando la base=L3,Entonces:

7. 𝐴 =
15𝑐𝑚 ∗ 18.5𝑐𝑚
2
A= 138.75cm2
10. Las medidas del trapecio mostrado en la figura son:
L1= (3.6+0.1) CM donde L1,L3, L4, son los lados del trapecio
L2= (2.9+0.1) CM y L2 es la altura
L3= (1.8+0.1) CM
L4= (2.0+0.1) CM
Calcular y expresar en forma correcta:
 El perímetro
P= L1+L4+L4+L3
P= 3.6cm+2.0cm+2.0cm+1.8cm

8. P= 9.4cm
 El area
𝑨 =
𝒉(𝒂 + 𝒄)
𝟐
Donde: h= L2 ; a=L1 ; c=L3
Entonces: 𝐴 =
2.9𝑐𝑚(3.6𝑐𝑚+1.8𝑐𝑚)
2
A= 7.83cm2
PRACTICA Nº 2
GRAFICOS
INTRODUCCIÓN
Las representaciones gráficas son indispensables para realizar un estudio tipo
experimental, ya que los mismos, nos generan una curva o una recta dependiendo de los
puntos que se grafiquen en el sistema de las coordenadas cartesianas (X, Y), generalmente
llamamos X a la variable independiente y Y a la variable dependiente.
Al momento de graficas logramos determinar el valor de algunas magnitudes
físicas, que generalmente están representadas por las pendientes de las rectas, no obstante,
el gráfico sirve para observar y comparar los resultados obtenidos con una curva teórica.
OBJETIVOS ESPECÍFICOS.
1. Determinar la ecuación o función que rige o gobierne un determinado fenómeno
o ley.
DATOS EXPERIMENTALES
GRAFICOS Nº1
NOTACION NORMAL NOTACION CIENTIFICA
F (grt) T (s) F (grt) T (s)
5.0 1.30 5.0x100 1.30x100
10.0 1.14 1.0x101 1.14x100
15.0 1.05 1.5x101 1.05x100

9. 20.0 0.99 2.0x101 9.9x10-1
Para m: tomamos dos puntos cualesquiera
𝑚 =
𝑙𝑜𝑔10− 𝑙𝑜𝑔5
𝑙𝑜𝑔1.14 − 𝑙𝑜𝑔1.30
𝑚 = −5.28
Por la gráfica buscamos 100 y vemos que su imagen K=18 aprox.
Así la ecuación es Y=17x-5.28
F=17t-5.28
GRAFICO Nº2
NOTACION NORMAL
I (µA) 22.8 14.5 9.2 5.8 3.7 2.3
T (s) 0 5 10 15 20 25
NOTACION CIENTIFICA
I (µA) 2.28x101 1.45x101 9.2x100 5.8x100 3.7x100 2.3x100
T (s) 0 5 10 15 20 25
Para hallar la ecuación buscamos C, para lo cual primero determinamos b y aun antes el
m.
𝑚 =
log(14.5) − log⁡(22.8)
5 − 0
𝑚 = −0.0393
B= antilog m= antilog (-0.0393) = 0.913

10. Como B=0.913 C=2.3logb = 2.3m
C=2.3log0.913 = -0.0903
Yo = 22.8 ; ya que esa es la imagen de X=0
Así Y=22.8e-0.0903x (genérica)
I=22.8e-0.0903t (experimental)
GRAFICO Nº3
NOTACIÓN NORMAL
T
(seg)
0 2 5 8 10 13 17 23 35 70 80 100
T (ºC) 120 116 111 107 104 101 96.9 91.8 83 67.2 63 57
NOTACIÓN CIENTIFICA
T
(s
eg
)
0x1
00
2x1
00
5x1
00
8x1
00
1x1
01
1.3x
101
1.7x
101
2.3x
101
3.5
x10
1
7x1
01
8x1
01
1x1
02
T
(º
C)
1.2
x10
2
1.16
x102
1.11
x102
1.07
x102
1.04
x102
1.01
x102
9.69
x101
9.18
x101
8.3
x10
1
6.72
x101
6.3
x10
1
5.7
x10
1
Dados los siguientes valores de Fuerza (Nw) y T(s). Aplicar mínimos cuadrados y
determinar la ecuación general que rige al fenómeno y grafíquela
T (s) X 0 1 2 3 4
F (Nw) Y 1 3 5 4 2
METODO DE MINIMOS CUADRADOS
X1 Y1 X1
2 X1Y1

11. 0 1 0 0
1 3 1 3
2 5 4 10
3 4 9 12
4 2 16 8
Σ 10 15 30 33
𝑚 =
𝑁𝛴𝑥𝑖𝑦𝑖 − 𝛴𝑥𝑖𝛴𝑦𝑖
𝑁𝛴𝑥𝑖² − (𝛴𝑥𝑖)²
𝑚 =
5(33)− 10(15)
5(30) − 10²
𝑚 =
3
10
𝑏 =
𝛴𝑦𝑖𝛴𝑥𝑖² − 𝛴𝑥𝑖𝛴𝑦𝑖𝑥𝑖
𝑁𝛴𝑥𝑖² − (𝛴𝑥𝑖)²
𝑏 =
15(30)− 10(33)
5(30)− 10²
𝑏 =
12
5
𝑌 = 𝑚𝑥 + 𝑏
𝑦 =
3
10
𝑥 +
12
5
⁡
GRAFICO Nº4
X 0 1 2 3 4 5
Y 12/5 27/10 3 33/10 18/5 39/10

12. CONCLUSIONES Y RECOMENDACIONES
Conclusiones:
GRAFICO 1: Graficando se obtuvo una curva en el papel milimetrado lo que indica que
se debe probar con otro tipo de papel, y como la gráfica es una curva potencial usaremos
el papel log-log.
Graficando en el log-log se obtuvo una recta por lo que se busca una ecuación tipo
Y= K.Xm, donde se buscan m y k para obtener la ecuación.
GRAFICO 2: Al graficas en papel milimetrado se observa que da una curva semejante a
una exponencial, por lo que se presume que debe corregir en papel semi-log; al graficas
en papel semi-log se observó la recta por lo que se está buscando una ecuación de la forma
Y=Yo . eex.
GRAFICO 3: Graficando en papel milimetrado nos dimos cuenta que es una curva de
tipo potencial y se debe corregir en papel log-log.
GRAFICO 4: En el gráfico 4 utilizamos el método de los mínimos cuadrados para
obtener m y b; y así obtener la ecuación de la gráfica de y obtener los valores de X y Y,
y al graficar en papel milimetrado nos dio una línea recta por lo que no fue necesario
hacer la corrección en otro tipo de papel.
Recomendaciones:
Al graficar los datos dados en papel milimetrado, debemos observar el tipo de gráfica que
obtenemos (Potencial o Exponencial), luego llevamos dichos datos a notación científica
para así graficar en papel log-log o semi-log según sea el caso.
Para esto debemos recordar que las gráficas de tipo exponencial se grafican en papel semi-
log y las de tipo potencial en papel log-log.