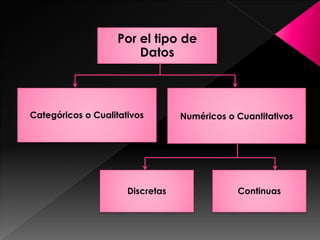
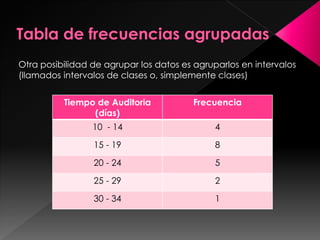
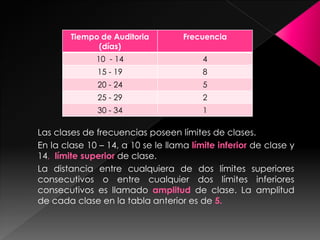
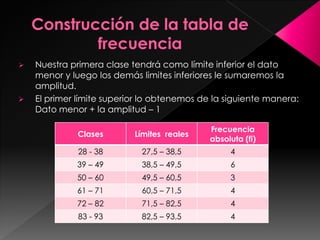
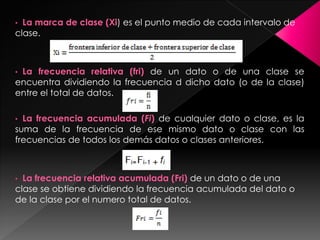
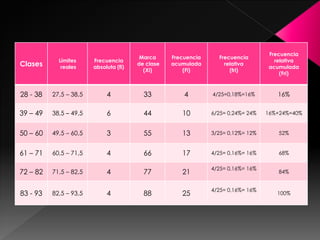
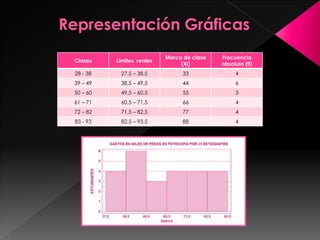
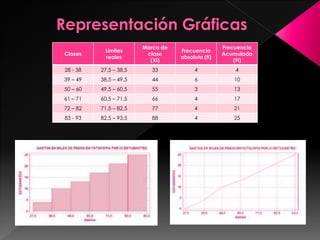
La estadística es la ciencia de los datos y su objetivo es mejorar la comprensión de los hechos a partir de la información disponible. Para lograrlo, los datos siempre deben ser organizados, clasificados y presentados de manera que facilite el análisis y las conclusiones válidas. Existen diferentes formas de organizar los datos, como tablas de frecuencias con datos agrupados y representaciones gráficas que transmiten la información de manera visual.