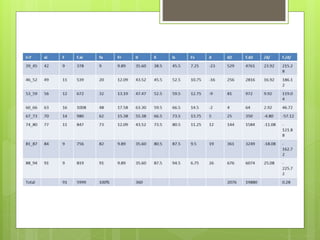
Este documento presenta definiciones estadísticas fundamentales como intervalo de confianza, frecuencia absoluta, frecuencia relativa, desviación estándar, media aritmética, moda y mediana. Explica conceptos como marca de clase, frecuencia acumulada, límite superior e inferior, y regla de Sturges para determinar el número de clases en un histograma. El documento provee fórmulas y ejemplos para calcular y aplicar estos conceptos estadísticos básicos.

1. ESCUELA NACIONAL DE CIENCIAS CONERCIALES SOLOLA
CATEDRATICO: OBED
ESTIDIANTE: KENDY ESTEFANY CHAVEZ YAC
CURSO: COMPUTACION
GRADO: 6to.PERITO CONTADOR
CLAVE:32
TRABAJA:TABLA DE VALORES

2. Intervalo de confianza
 Intervalo

 Las líneas verticales representan 50 construcciones diferentes de
intervalos de confianza para la estimación del valor μ.
 En estadística, se llama a un par o varios pares de números entre
los cuales se estima que estará cierto valor desconocido con una
determinada probabilidad de acierto. Formalmente, estos
números determinan un intervalo, que se calcula a partir de datos
de una muestra, y el valor desconocido es un parámetro
poblacional. La probabilidad de éxito en la estimación se
representa con 1 - α y se denomina nivel de confianza. En estas
circunstancias, α es el llamado error aleatorio o nivel de
significación, esto es, una medida de las posibilidades de fallar en
la estimación mediante tal intervalo.

3. La marca de clase

 La marca
 Es el punto medio de cada intervalo.
 La marca de clase es el valor que
representa a todo el intervalo para
el cálculo de algunos parámetros como
la media aritmética o la desviación típica.
 Se representa por ci o xi.

4. Frecuencia estadística

 Frecuencia
 Para el término en física,
véase Frecuencia.
 Se denomina frecuencia a la cantidad
de veces que se repite un determinado
valor de la variable.
 Se suelen representar
con histogramas y diagramas de Pareto.

5. La frecuencia absoluta
 La frecuencia absoluta
 Es el número de veces que aparece un
determinado valor en un estudio
estadístico.
 Se representa por fi.
 La suma de las frecuencias absolutas es
igual al número total de datos, que se
representa por N.

6. Para indicar resumidamente estas sumas se utiliza la letra griega Σ(sigma mayúscula) que se lee
suma o sumatoria.

7. La frecuencia acumulada
 La frecuencia acumulada es la suma de las
frecuencias absolutas de todos los valores
inferiores o iguales al valor considerado.
 La frecuencia acumulada se representa por Fi.
 Ejemplo
 Durante el mes de julio, en una ciudad se han
registrado las siguientes temperaturas máximas:
 32, 31, 28, 29, 33, 32, 31, 30, 31, 31, 27, 28, 29, 30,
32, 31, 31, 30, 30, 29, 29, 30, 30, 31, 30, 31, 34, 33,
33, 29, 29.

8. La frecuencia relativa
 La frecuencia relativa es el cociente entre
la frecuencia absoluta de un
determinado valor y el número total de
datos.
 La frecuencia relativa se puede expresar
en tantos por ciento y se representa
por ni.

9. El grado sexagesimal
 El grado sexagesimal,
 como unidad del sistema de medida de ángulos
sexagesimal, está definido partiendo de que un
ángulo recto tiene 90° (90 grados sexagesimales),
y sus divisores: el minuto sexagesimal y el segundo
sexagesimal, están definidos del siguiente modo:
 1 ángulo recto = 90° (grados sexagesimales).
 1 grado sexagesimal = 60′ (minutos
sexagesimales).
 1 minuto sexagesimal = 60″ (segundos
sexagesimales).

10. Límite superior y límite inferior

 Límite superior y límite inferior
 En matemática se define límite
superior y límite inferior de una sucesión (xn)
como el mayor y menor límite convergente
de las subsecuencias de (xn). Análogamente
a éste, el límite superior y límite inferior
para funciones reales se define de la misma
manera. El límite superior y el límite inferior son
un sustituto parcial para el límite, si es que
éste no existe.

11. Definición formal
Formalmente el límite inferior de una sucesión se define como
o también como
y se denota como o como . Análogamente se
define .
Estas definiciones son útiles en un conjunto parcialmente ordenado en un sentido cuantitativo,
y proporcionan que el supremo y el ínfimoexistan. En una red reticular completa siempre
existen estos valores, por lo que en este caso, cada secuencia tiene un límite inferior y límite
superior asociado.
Si existe el límite inferior y el límite superior de una sucesión , se cumple
que

12. CURVAS DE FRECUENCIAS
 CURVAS DE FRECUENCIAS. OJIVAS SUAVIZADAS
 El conjunto de datos puede considerarse normalmente
como perteneciente a una muestra extraída de
una población grande. A causa de las muchas
observaciones que podemos realizar en la población es
posible teóricamente (para datos continuos) elegir los
intervalos de clase muy pequeños y todavía tener un
número adecuado de observaciones dentro de cada
clase. Así se tiene que el polígono de frecuencias o el de
frecuencias relativas para una población grande puede
estar formado por muchos pequeños segmentos rectos
que aproximan el conjunto a una curva, las curvas de este
tipo pueden llamarse curvas de frecuencias o curvas de
frecuencias relativas, respectivamente.

13. La desviación típica o desviación estándar (denotada con el símbolo σ o s, dependiendo de la
procedencia del conjunto de datos) es una medida de dispersión para variables de razón (variables
cuantitativas o cantidades racionales) y de intervalo. Se define como la raíz cuadrada de
la varianza de la variable.
FRECUENCIA Y DESVIACION CUADRADA
La desviación estándar o desviación típica es la raíz cuadrada de la varianza.
Es decir, la raíz cuadrada de la media de los cuadrados de las puntuaciones de desviación.
Desviación en valor absoluto
La desviación respecto a la media es la diferencia en valor absoluto entre
cada valor de la variable estadística y la media aritmética.
FRECUENCIA Y DESVIACION EN VALOR ABSOLUTO
La desviación media es la media aritmética de los valores absolutos
de las desviaciones respecto a la media.
La desviación media se representa por

14. Regla de Sturges
Regla de Sturges
La regla de Sturges, propuesta por Herbert Sturges en 1926, es una regla práctica acerca del
número de clases que deben considerar al elaborarse un histograma.1
Este número viene dado por la siguiente expresión:
, donde M es el tamaño de la muestra.
Que puede pasarse a logaritmo base 10 de la siguiente forma:
siendo N la cantidad de datos.
El valor de c (número de clases) es común redondearlo al entero más cercano.

15. MEDIA ARITMÉTICA SIMPLE
Datos Agrupados
MEDIA ARITMÉTICA SIMPLE
La media aritmética o promedio simple ( X ) muestra el valor central de los datos constituyendo
ser la medida de ubicación que más se utiliza. En general, es calculada sumando los valores de
interés y dividiendo entre el número de valores sumados.
Datos Agrupados
La fórmula correspondiente para su cálculo es la siguiente: n n n f f f f f X f X f X f X X + + + + + + + =
1 2 3 1 1 2 2 3 3 _ ... ¿Cuándo se debería utilizar este tipo de media? Para responder a esta
interrogante se presentan una ilustración sobre la aplicación de esta medida de tendencia central.

16. LA MODA
Mediana
 LA MODA
 La moda es el valor que tiene mayor frecuencia absoluta.
 Se representa por Mo.
 Se puede hallar la moda para variables cualitativas ycuantitativas.
 Hallar la moda de la distribución


 Mediana
 Es el valor que ocupa el lugar central de todos los datos cuando
éstos están ordenados de menor a mayor.
 La mediana se representa por Me.
 La mediana se puede hallar sólo para variables cuantitativas.

