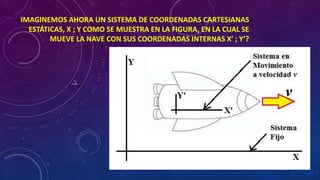
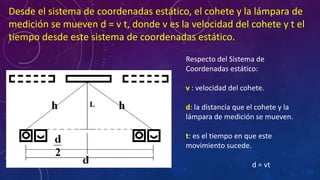
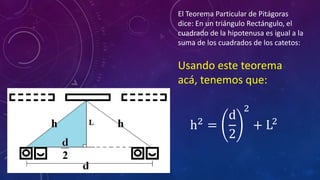
La paradoja de los gemelos describe cómo dos gemelos experimentan el paso del tiempo de manera diferente cuando uno de ellos realiza un viaje espacial a alta velocidad. El gemelo que viaja en una nave espacial a velocidades cercanas a la de la luz envejece menos que su gemelo que permanece en la Tierra. La teoría de la relatividad explica que el tiempo es relativo y depende del movimiento, por lo que los gemelos medirán tiempos diferentes entre los mismos eventos.

1. PARADOJA DE LOS GEMELOS
Una mirada matemática introductoria.
Primer intento de clase inagural del 2do Medio - 2015

2. ¿MARCO DE LA PARADOJA DE LOS GEMELOS?
• La paradoja de los gemelos (o de los relojes) es un experimento mental que analiza la
distinta percepción del tiempo entre dos observadores con diferentes estados de
movimiento.
• Esta paradoja fue propuesta por Einstein al desarrollar lo que hoy se conoce como la
relatividad especial.
• Dicha teoría postula que la medida del tiempo no es absoluta, y que, dados dos
observadores, el tiempo medido entre dos eventos por estos observadores, en general,
no coincide, sino que la diferente medida de tiempos depende del estado de movimiento
relativo entre ellos. Así, en la teoría de la relatividad, la medida del tiempo (y espacio) son
relativas, pues dependen del estado de movimiento del observador.

3. ¿QUÉ DICE LA PARADOJA DE LOS GEMELOS?
EN LA FORMULACIÓN MÁS HABITUAL DE LA PARADOJA, DEBIDA A
PAUL LANGEVIN, SE TOMA COMO PROTAGONISTAS A DOS GEMELOS
(DE AHÍ EL NOMBRE);
EL PRIMERO DE ELLOS HACE UN LARGO VIAJE A UNA ESTRELLA EN UNA
NAVE ESPACIAL A VELOCIDADES CERCANAS A LA VELOCIDAD DE LA
LUZ; EL OTRO GEMELO SE QUEDA EN LA TIERRA.
A LA VUELTA, EL GEMELO VIAJERO ES MÁS JOVEN QUE EL GEMELO
TERRESTRE.

4. EN IMÁGENES ….

5. ENCONTREMOS UNA RELACIÓN ENTRE LO QUE
PASA CON EL TIEMPO PARA EL GEMELO
VIAJERO Y PARA EL GEMELO EN TIERRA.
Imaginemos que dentro de la nave que
viaja a velocidad “v”, establecemos un
sistema de Coordenadas Cartesianas
X’ ; Y’
como se muestra en la figura:
Materia: Coordenadas Cartesianas, 1ro. Medio.

6. IMAGINEMOS AHORA UN SISTEMA DE COORDENADAS CARTESIANAS
ESTÁTICAS, X ; Y COMO SE MUESTRA EN LA FIGURA, EN LA CUAL SE
MUEVE LA NAVE CON SUS COORDENADAS INTERNAS X’ ; Y’?

7. ¿QUÉ QUEREMOS HACER?
1) DEJAR UN GEMELO EN TIERRA.
2) MANDAR AL OTRO GEMELO EN VIAJE
ESPACIAL, A UNA VELOCIDAD CERCANA
A LA DE LA LUZ (ESTO ES SOLO UN
EXPERIMENTO MENTAL)
3) VER LA RELACIÓN ENTRE EL TIEMPO
EN VIAJE Y EL TIEMPO EN TIERRA,
PARA CORROBORAR QUE EL TIEMPO ES
RELATIVO, PUES LA MEDICIÓN DEL
MISMO ENTRE DOS EVENTOS,
DEPENDERÁ DE LA VELOCIDAD
RELATIVA EN LA QUE SE MUEVAN LOS
DOS OBSERVADORES.

8. VAMOS A INTRODUCIR ARRIBA DE LA NAVE ESPACIAL, UN RELOJ LUMINOSO,
EL PROTOTIPO DISEÑADO POR EL FÍSICO ESTADOUNIDENSE R.P. FEYNMAN.
LA AMPOLLETA EMITE PULSACIONES REGULARES QUE REBOTAN EN EL ESPEJO
VOLVIENDO AL CONTADOR PARA PROVOCAR UN CLICK.

9. • Sea t’ el tiempo transcurrido entre dos clicks
al interior del sistema en movimiento.
Este tiempo lo calculamos usando la fórmula de
la velocidad:
𝑣 =
𝑑
𝑡
Desde donde despejamos:
𝑡′ =
2𝐿
𝑐
El tiempo t’ es de ida y vuelta. La Luz
(cuya velocidad es c) recorre dos veces
la distancia “L”.
t =
d
v
En nuestro caso: Materia: Despeje
de fómula, 8avo.

10. Pero desde el Sistema de
Coordenadas estático, la
imagen del reloj luminoso es
otra, porque el cohete ha
avanzado a la velocidad “v”
t =
ℎ
𝑐
+
ℎ
𝑐
=
2ℎ
𝑐
La velocidad sigue siendo la
de la luz, la distancia de ida
y la de vuelta son iguales a
“h” y el tiempo desde el
sistema estático es “t”:
Materia:
Suma Fracciones Igual Denominador, 4to. Básico

11. Desde el sistema de coordenadas estático, el cohete y la lámpara de
medición se mueven d = v t, donde v es la velocidad del cohete y t el
tiempo desde este sistema de coordenadas estático.
Respecto del Sistema de
Coordenadas estático:
v : velocidad del cohete.
d: la distancia que el cohete y la
lámpara de medición se mueven.
t: es el tiempo en que este
movimiento sucede.
d = vt

12. El Teorema Particular de Pitágoras
dice: En un triángulo Rectángulo, el
cuadrado de la hipotenusa es igual a la
suma de los cuadrados de los catetos:
Usando este teorema
acá, tenemos que:
h2
=
d
2
2
+ L2

13. Pero antes teníamos que: t =
2h
c
; despejando: h =
ct
2
d = vt ; o lo mismo:
d
2
=
vt
2
t′ =
2L
c
; despejando: L =
ct′
2
Luego nuestra ecuación es:
ct
2
2
=
vt
2
2
+
ct′
2
2
Despejemos t en función de t’

14. ct
2
2
=
vt
2
2
+
ct′
2
2
𝑐2 𝑡2
4
=
𝑣2 𝑡2
4
+
𝑐2 𝑡′2
4
; Multiplicando la ecuación por 4:
𝑐2 𝑡2 = 𝑣2 𝑡2 + 𝑐2 𝑡′2; Trasponiendo términos:
𝑐2 𝑡2 − 𝑣2 𝑡2 = 𝑐2 𝑡′2 ; 𝐟𝐚𝐜𝐭𝐨𝐫𝐚𝐧𝐝𝐨 𝐩𝐨𝐫 𝐭 𝟐
𝑡2 𝑐2 − 𝑣2 = 𝑐2 𝑡′2 ; Dividiendo por 𝑐2
𝑡2
1 −
𝑣2
𝑐2 = 𝑡′2
; Despejando y Tomando Raíz:
𝑡 =
𝑡′
2
1 −
𝑣2
𝑐2
Maravilloso !!!! ,
tenemos una ecuación
que vincula:
el tiempo en el sistema de
coordenadas móvil
(en la nave que vuela)
con
el tiempo en el sistema de
coordenadas estático
(en la tierra)
LOS TIEMPOS SON DIFERENTES!
(El tiempo es relativo, producto
del movimiento)
Materia: Manejo del Lenguaje Algebraico + Potencias.

15. PROBLEMA:
Uno de los gemelos de LEO, se lanza en un cohete a 8/10 de
la velocidad de la luz respecto de la tierra. Luego de
transcurridos 30 años en el cohete, ¿Cuánto tiempo
transcurrió en la tierra? t’ : Tiempo transcurrido en el cohete.
V : velocidad del cohete = 8c/10
𝑡 =
30 𝑎ñ𝑜𝑠
2
1 −
0,8𝑐 2
𝑐2
=
30 𝑎ñ𝑜𝑠
2
1 − 0,64
=
𝑡 =
30 𝑎ñ𝑜𝑠
0,6
= 50 𝑎ñ𝑜𝑠
Mientras el LEO que viaja lo hace por 30 años, en la tierra han transcurridos 50 años. Eso
muestra que entre dos sucesos: la partida y la llegada de un cohete, dos observadores han
medido 2 tiempos diferentes: el tiempo es Relativo!, cuando uno de esos observadores se
mueve respecto del otro a cierta velocidad, mientras el cohete se mueve con rapidez cercana
de la rapidez de la LUZ.
Materia: Aplicación a un Problema
Concreto.