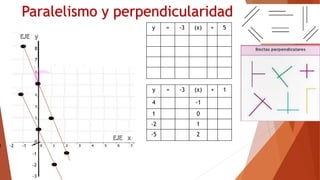
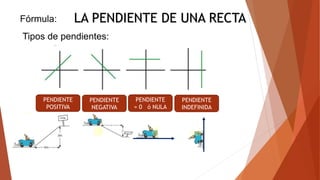
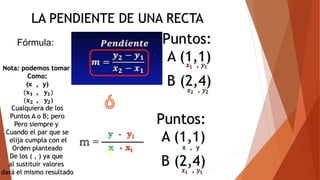
Este documento presenta información sobre la representación algebraica y gráfica de relaciones geométricas. Explica los sistemas de coordenadas cartesianas y cómo usarlos para representar funciones algebraicas en un plano. También define conceptos como pendiente, paralelismo y perpendicularidad, y muestra ejemplos de cómo calcular la pendiente entre dos puntos y usar la ecuación punto-pendiente.

1. REPRESENTACIÓN ALGEBRAICA Y GRÁFICA DE RELACIONES
RESULTADO DE APRENDIZAJE
1.1 Representa la solución de problemas geométricos mediante el análisis de las variables
Objetivos de la sesión
Que los estudiantes Caractericen de forma analítica los problemas
geométricos de localización y trazado de lugares geométricos.
UNIDAD 1
Aplicación de los sistemas de coordenadas rectangulares.
Propósito del módulo
Utilizar los sistemas coordenados de representación por medio de la
ubicación de funciones algebraicas en el plano, a través de estrategias sobre
el tratamiento de los lugares geométricos, para incorporar métodos analíticos
en la resolución de problemas geométricos.
Tema:
Sistema Cartesiano De Coordenadas

3. REPRESENTACIÓN ALGEBRAICA Y GRÁFICA DE RELACIONES
RESULTADO DE APRENDIZAJE
1.2 Traza en un plano los puntos, ejes y cuadrantes mediante las coordenadas de los lugares
geométricos en los diferentes contextos en los que se desarrolla.
Objetivos de la sesión
Que los estudiantes Ubiquen en el plano - en distintos cuadrantes - y
localizan puntos en los ejes y los cuadrantes mediante sus coordenadas.
UNIDAD 1
Aplicación de los sistemas de coordenadas rectangulares.
Propósito del módulo
Utilizar los sistemas coordenados de representación por medio de la
ubicación de funciones algebraicas en el plano, a través de estrategias sobre
el tratamiento de los lugares geométricos, para incorporar métodos analíticos
en la resolución de problemas geométricos.
Tema:
Representación gráfica de la pendiente de una recta y
Representación algebraica y gráfica de la recta.

4. Paralelismo y perpendicularidad
y = -3 (x) + 5
8
7
3 -2 -1
-1
-2
-3
y = -3 (x) + 1
4 -1
1 0
-2 1
-5 2

5. LA PENDIENTE DE UNA RECTA
O ALTURA
PENDIENTE = la inclinación
y dirección de rectas.
Elevación = 2
Empieza en un punto en la recta, como (2, 1) y
muévete verticalmente hasta alinearte con otro
punto en la recta, como (6, 3). La elevación es
de 2 unidades. Es positiva puesto que te
moviste hacia arriba.
Avance = 4
Luego, muévete horizontalmente al punto (6, 3).
Cuenta el número de unidades. El avance es de
4 unidades. Es positivo puesto que te moviste
hacia la derecha
PENDIENTE=
PENDIENTE=
2
4
=
1
2
1
2
Pendiente =
𝑒𝑙𝑒𝑣𝑎𝑐𝑖ó𝑛
𝑎𝑣𝑎𝑛𝑐𝑒
m
m

6. LA PENDIENTE DE UNA RECTA
Fórmula:
Tipos de pendientes:
PENDIENTE
POSITIVA
PENDIENTE
NEGATIVA
PENDIENTE
= 0 ó NULA
PENDIENTE
INDEFINIDA

7. LA PENDIENTE DE UNA RECTA
Fórmula:
B (2,4)
Puntos:
A (1,1)
B (2,4)
Puntos:
A (1,1)
Nota: podemos tomar
Como:
(x , y)
(𝐱𝟏 , 𝐲𝟏)
(𝐱𝟐 , 𝐲𝟐)
Cualquiera de los
Puntos A o B; pero
Pero siempre y
Cuando el par que se
elija cumpla con el
Orden planteado
De los ( , ) ya que
al sustituir valores
dará el mismo resultado

8. LA PENDIENTE DE UNA RECTA
B (2,6)
Puntos:
A (3,8)
cuál es el valor de la pendiente si conocemos los siguientes puntos:
(3,8) y (2, 6). En este caso conocemos los dos puntos por lo que
utilizamos la ecuación de pendiente
Fórmula:
Sustituir:

9. La ecuación punto pendiente
La ecuación punto – pendiente es útil cuando conocemos un punto y el valor de la
pendiente, y sirve para determinar el grado de inclinación que tiene nuestra recta.
Ejemplo: determinar la ecuación punto – pendiente si conocemos el punto (3,5) y el
valor de la pendiente es 4.
Fórmula:
Sustituir:
Se iguala a cero (0) la ecuación
Se reducen términos semejantes
Puntos:
A ( , )
B (3,5)
Se ordenan términos
M= 4: