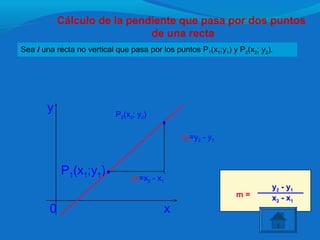
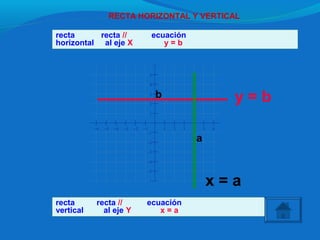
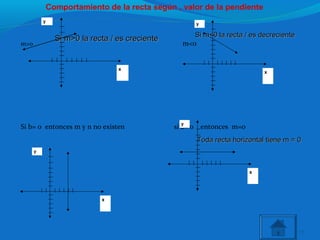
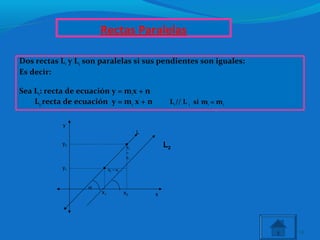
Este documento describe conceptos matemáticos relacionados con la ecuación de la recta, incluyendo la pendiente, ecuaciones de rectas horizontales y verticales, paralelismo, perpendicularidad y posiciones relativas de rectas. Explica cómo calcular la pendiente de una recta a partir de dos puntos y cómo identificar el comportamiento de una recta según el valor de su pendiente.

1. Lcdo. Juan Jácome.

2. INDICE
1.-Objetivos
2.-Explicar el concepto de pendiente.
3.-Cálculo de la pendiente de una recta
6.-Pendiente y coeficiente de posición de la recta
7.-Recta horizontal y vertical
5.-Ecuación de la recta , a través de la forma punto pendiente
8.-Ecuación de la recta , forma general
9.-Ecuación Principal de la Recta principal de la recta
10.-Comportamiento de la recta según valor de la pendiente
11.-Como encontrar la pendiente de una recta a través de su grafica
12.-Posiciones relativas de dos rectas en el plano
13.-Rectas paralelas
14.-Grafica de dos rectas paralelas
15.-Rectas perpendiculares
16.-Grafica de rectas PERPENDICULARES
17.-Rectas coincidentes

3. OBJETIVO FUNDAMENTAL Conocer y utilizar conceptos matemáticos asociados
al estudio de la ecuación de la recta, sistemas de ecuaciones lineales, semejanzas
de figuras planas y nociones de probabilidad, iniciándose en el reconocimiento y
aplicación de modelos matemáticos.
3
CONTENIDOS MINIMOS OBLIGATORIOS
• Ecuación de la recta.
• Interpretación de la pendiente y del intercepto con el eje de las ordenadas.
• Condición de paralelismo y perpendicularidad.
Objetivos de Aprendizaje
1) Reconocer la expresión algebraica y la gráfica de la ecuación de la recta.
2) Identificar e interpretar los parámetros de pendiente e intercepto con el eje de las
ordenadas tanto en la forma y = mx como en ax + by + c=0 de la ecuación de la recta.
3) Reconocer la pendiente y el intercepto con el eje de las ordenadas en las respectivas
gráficas.
4) Analizar las posiciones relativas que pueden tener dos rectas en el plano.
5) Establecer las relaciones específicas que condicionan el paralelismo y la perpendicularidad
entre rectas.
.

4. La pendiente de una recta en un sistema de
representación triangular (de un plano
cartesiano ), suele ser representado por la
letra , y es definido como el cambio o diferencia
en el eje Y dividido por el respectivo cambio en
el eje X, entre 2 puntos de la recta. En la
siguiente ecuación se describe:
DEFINICION DE PENDIENTE

5. y2 - y1
x2 - x1
Cálculo de la pendiente que pasa por dos puntos
de una recta
0 x
y
P1(x1;y1)
P2(x2; y2)
∆x=x2 - x1
∆y=y2 - y1
m =
Sea l una recta no vertical que pasa por los puntos P1(x1;y1) y P2(x2; y2).

6. La ecuación de la recta de pendiente m, y un punto de Ella (xLa ecuación de la recta de pendiente m, y un punto de Ella (x11, y, y11) es:) es:
(x1, y1) y - y1 = m(x - x1)
X
Y
Ecuación de la recta, a través de la forma punto
pendiente: y-y1=m (x-x1)

7. La gráfica de una recta de pendiente m y ordenada en el origen
b, es:
b
y = mx + b
X
Y
Pendiente y coeficiente de posicion de la recta .
•Ecuación pendiente ordenada al origen y = m x+b

8. recta recta // ecuación
horizontal al eje X y = b
recta recta // ecuación
vertical al eje Y x = a
−6 −5 −4 −3 −2 −1 1 2 3 4 5 6
−6
−5
−4
−3
−2
−1
1
2
3
4
5
b
a
y = b
x = a
RECTA HORIZONTAL Y VERTICAL

9. 9
Es toda igualdad de la forma ax + by = c , donde a,b,c ∈ R, representa una
ecuación lineal con dos incógnitas llamada ecuación General de la Recta, las soluciones
son pares ordenados de la forma (x, y). Este par ordenado (x, y) corresponde a un
punto del plano cartesiano.
1-1
1
-1
2
2
3
3
4
4
5
•
•
L
x
yEjemplo Nº1 : la ecuación L: x + y - 4 = 0 es la ecuación
general de la recta.
Grafiquemos L en el plano cartesiano:
Tabla de valores Gráfico
X Y (x, y)
2 2 (2, 2)
1 3 (1, 3)
0 4 (0, 4)
-1 5 (-1, 5)
Observaciones:
1. A toda ecuación lineal (de primer grado) con dos incógnitas le corresponde gráficamente una
recta.
• Cada par ordenado de números (x, y) corresponde a las coordenadas de un punto que es
solución de la ecuación dada, es decir satisface esta ecuación.
•Forma general Ax + By + C = 0

10. Ecuación Principal de la Recta
Importante
Tiene la forma y= mx + n y se llama ecuación principal de la recta
donde mes la pendiente de la recta ( ángulo de inclinación de la recta respecto el eje x)
y n es el intercepto con el eje y eje de las ordenadas o el punto donde la recta corta al eje y.
Ecuación General
2x – y- 1 = 0
Despejemos “y” en términos de “x” - y = - 2x + 1
Si dividimos la igualdad por -1 para
que el coeficiente de y no sea
negativo
-Y = -2x + 1 / : - 1
Nos queda Y = 2x – 1
se llama Ecuación principal de la recta.
Donde: m = 2 n= -1
10
Ejemplo: Sea L2
una recta en el plano cuya ecuación es: 2x – y – 1 = 0
Despejemos ”y” en la ecuación, para darle la forma principal.

11. m>0 m<0
Si b= 0 entonces m y n no existen si a= 0 entonces m=o
11
x
y
x
y
x
y
x
y
Si m>0 la rectaSi m>0 la recta ll es crecientees creciente Si m<0 la rectaSi m<0 la recta ll es decrecientees decreciente
Toda recta horizontal tiene m = 0Toda recta horizontal tiene m = 0
Comportamiento de la recta según , valor de la pendiente

12. ¿Cómo encontrar la pendiente de una recta a través de una
grafica?
Ejemplo: Si tenemos la gráfica de una recta y queremos calcular la pendiente, ubica
dos puntos del plano que pertenezcan a la recta.
Por ejemplo:
Los puntos ( 2,2) y (-1,5) pertenecen a la recta
Usaremos la ecuación
12
x-x
y-y
m
12
12
=
donde (x1 , y1) son las coordenadas de uno de los puntos que pertenece a la recta.
( x2 , y2) son las coordenadas del otro punto que pertenece a la recta.
Por lo tanto remplazando tenemos:
Luego la pendiente m = -1
m = = = = -1
12
12
xx
yy
−
−
21
25
−−
−
3
3
−
1-1
1
-1
2
2
3
3
4
4
5
•
•
L
x
y

13. Posiciones relativas de dos rectas en el plano
Dos rectas L1 y L2 en el plano pueden adoptar 3 posiciones:
a) Que sean Paralelas b) Que se intercepten
c) Que sean
Coincidentes
13
1-1
1
-1
2
2
3
3
4
4
5
•
•
L
x
y
1-1
1
-1
2
2
3
3
4
4
5
•
•
L
x
y
1-1
1
-1
2
2
3
3
4
4
5
•
•
L
x
y

14. Rectas Paralelas
Dos rectas L1 y L2 son paralelas si sus pendientes son iguales:
Es decir:
Sea L1: recta de ecuación y = m1x + n
L2:recta de ecuación y = m2 x + n L1// L 2 si m1 = m2
14
x1 x2
y1
y2
L
•
•
x2 – x1
y2
–
y1
α
x
y
L2

15. Ejemplo
Grafiquemos las rectas de ecuaciones
y = x y = x – 2 y = x + 1 y = x - 3
En el mismo plano cartesiano
15

16. Rectas Perpendiculares
Dos rectas que se cortan en un punto cualquiera se llaman
rectas secantes, pero si además de cortarse en un punto, ambas
rectas forman un ángulo recto ( de 90º), se dice que son
perpendiculares.
si L1 es una recta de ecuación
y=m1 x + n
L2 es una recta de ecuación
y= m2x +n
L1 L┴ 2 si m1 • m2 = -1
16
x1 x2
y1
y2
L
•
•
x2 – x1
y2
–
y1
α
x
y
L1

17. GRAFICA DE RECTAS PERPENDICULARES
Grafiquemos las rectas de ecuaciones
y = 4x + 3
y = - ¼ x + 1 En el mismo plano cartesiano
17

18. 18
Rectas Coincidentes
Rectas coincidentes: Si L1 y L2 son coincidentes entonces sus
pendientes m1 y m2 son iguales y su intercepto con el eje de ordenadas
“n” en ambas rectas son iguales es decir las rectas coinciden punto a
punto.
Si L1: y = m1 x + n1
L2: y = m2 x + n2
L1 y L2 son coincidentes entonces m1 = m2 y
n1 = n2 L1 y L2 son la misma recta.
x1 x2
y1
y2
L1
•
•
α
x
y
L2