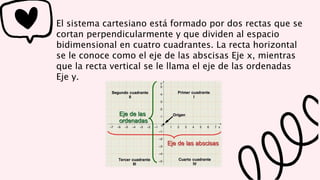
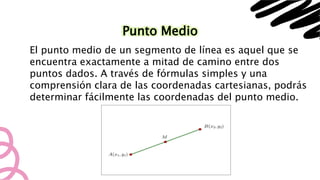
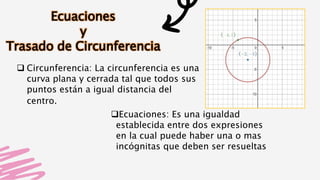
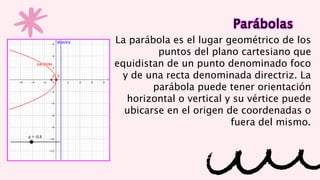
El documento explica el plano cartesiano y sus componentes principales. Describe el sistema de coordenadas cartesianas formado por dos rectas perpendiculares que dividen el plano en cuadrantes. Explica cómo calcular la distancia entre puntos y encontrar el punto medio de un segmento usando coordenadas. También define figuras geométricas como circunferencias, parábolas, elipses e hipérbolas y cómo representarlas gráficamente a través de ecuaciones.

1. Plano Numérico
Republica Bolivariana de Venezuela
Ministerio del Poder Popular Para la Educación
Universidad Politécnica Territorial Andrés Eloy Blanco
Barquisimeto Edo. Lara
Estudiante: Daianara Reyes
Sección: T0232
Cedula: 31099616

2. Plano Numérico
Se conoce como plano cartesiano, coordenadas cartesianas o
sistema cartesiano, a dos rectas numéricas perpendiculares, una
horizontal y otra vertical, que se cortan en un punto llamado origen
o punto cero.
La finalidad del plano cartesiano es describir la posición o
ubicación de un punto en el plano, la cual está representada por el
sistema de coordenadas.
El plano cartesiano también sirve para analizar matemáticamente
figuras geométricas como la parábola, la hipérbole, la línea, la
circunferencia y la elipse, las cuales forman parte de la geometría
analítica.

3. El sistema cartesiano está formado por dos rectas que se
cortan perpendicularmente y que dividen al espacio
bidimensional en cuatro cuadrantes. La recta horizontal
se le conoce como el eje de las abscisas Eje x, mientras
que la recta vertical se le llama el eje de las ordenadas
Eje y.

4. Distancia
A partir de conocer la ubicación de dos
puntos en el plano cartesiano, es posible
determinar la distancia que hay entre
éstos. Cuando algún punto se encuentra
en el eje de las x o de las abscisas o en
una recta paralela a éste eje, la distancia
entre los puntos corresponde al valor
absoluto de las diferencia de sus abscisas.
(x 2 – x 1 ).

5. Formula para Calcular
Distancia
La fórmula para calcular dicha magnitud está
dada por la siguiente expresión:

6. Punto Medio
El punto medio de un segmento de línea es aquel que se
encuentra exactamente a mitad de camino entre dos
puntos dados. A través de fórmulas simples y una
comprensión clara de las coordenadas cartesianas, podrás
determinar fácilmente las coordenadas del punto medio.

7. Ecuaciones
y
Trasado de Circunferencia
❑ Circunferencia: La circunferencia es una
curva plana y cerrada tal que todos sus
puntos están a igual distancia del
centro.
❑Ecuaciones: Es una igualdad
establecida entre dos expresiones
en la cual puede haber una o mas
incógnitas que deben ser resueltas

8. Parábolas
La parábola es el lugar geométrico de los
puntos del plano cartesiano que
equidistan de un punto denominado foco
y de una recta denominada directriz. La
parábola puede tener orientación
horizontal o vertical y su vértice puede
ubicarse en el origen de coordenadas o
fuera del mismo.

9. Eclipses
Una elipse es el lugar geométrico de todos
los puntos de un plano para los cuales se
cumple que el cociente entre sus distancias
a un punto fijo (que se denomina foco) y a
una recta dada (llamada directriz)
permanece constante y es igual a la
excentricidad de la misma.

10. Hipérbola
Al igual que la elipse, la hipérbola también se puede
definir como un conjunto de puntos en el plano de
coordenadas. Una hipérbola es el conjunto de todos
los puntos ( x , y ) ( x , y ) en un plano tal que la
diferencia de las distancias entre ( x , y ) ( x , y ) y los
focos es una constante positiva

11. Representar gráficamente la ecuación
de la cónica
✓ Circunferencia: (x-c 1)2+(y-c2)2=r.
✓ Elipse: (x2/a2)+(y2/b2)=1.
✓ Parábola: x2=2py.
✓ Hipérbola: -2x²+y²+xy+2x+2y+1=0.
Una cónica es la curva obtenida como
intersección de un plano, llamado plano de
corte, con la superficie de un cono doble
(un cono con dos nudos)

12. Ejercicio Propuesto:
Ubicar los siguientes puntos en
el plano cartesiano:
A (5; 3)
B (-4; -2)
C (-2; 0)