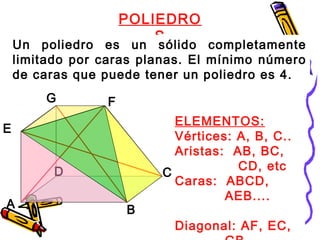
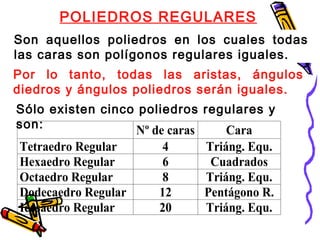
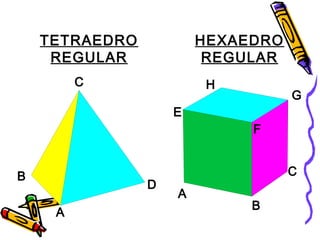
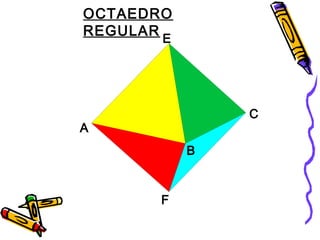
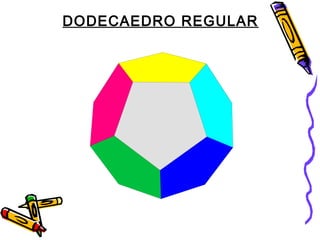
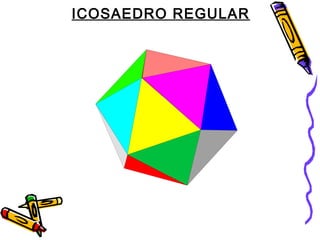
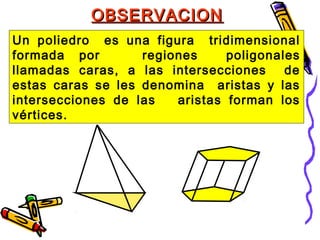
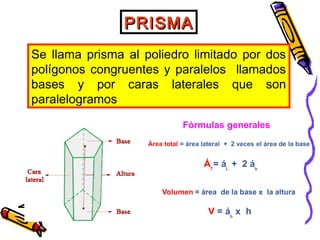
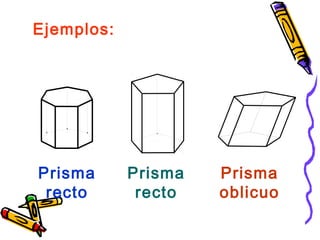
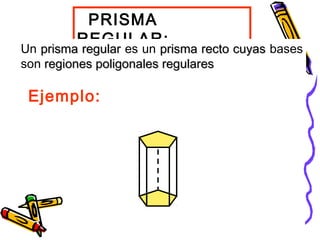
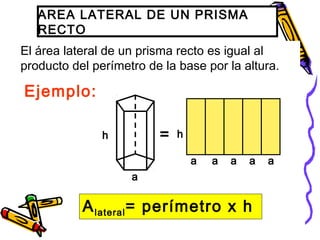
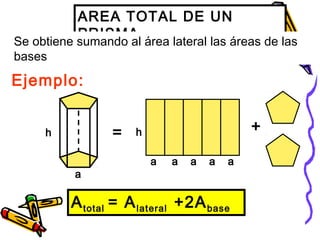
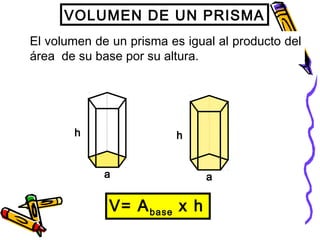
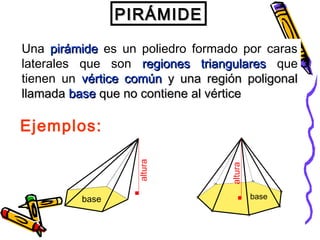
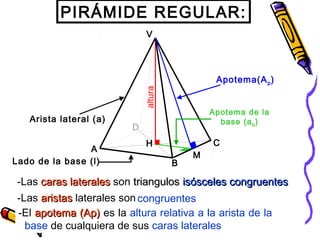
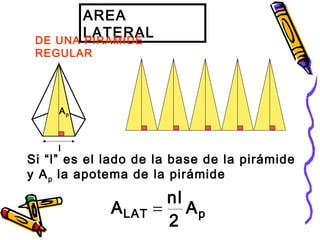
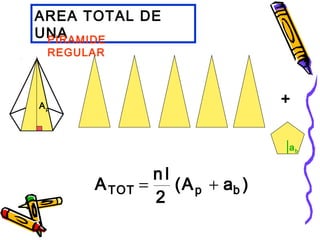
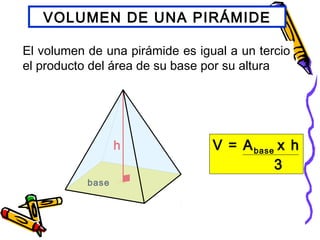
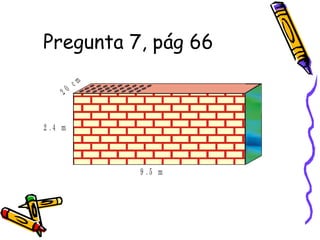
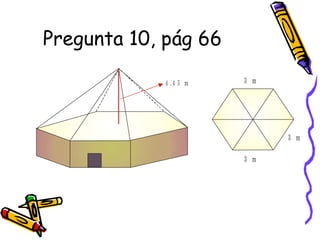
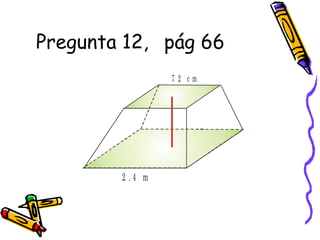
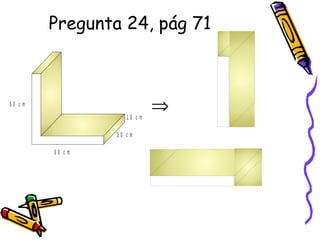
Este documento trata sobre poliedros y sus propiedades. Explica que un poliedro es un sólido limitado por caras planas, y que los poliedros regulares son aquellos donde todas las caras son polígonos regulares iguales. Describe las propiedades de figuras como el prisma, la pirámide y los cinco poliedros regulares.

1. MATEMÁTICAMATEMÁTICA
BÁSICABÁSICA
ComunicadoresComunicadores
POLIEDROSPOLIEDROS

2. POLIEDRO
S
Un poliedro es un sólido completamente
limitado por caras planas. El mínimo número
de caras que puede tener un poliedro es 4.
D
A B
C
E
FG
ELEMENTOS:
Vértices: A, B, C..
Aristas: AB, BC,
CD, etc
Caras: ABCD,
AEB....
Diagonal: AF, EC,

3. POLIEDROS REGULARES
Son aquellos poliedros en los cuales todas
las caras son polígonos regulares iguales.
Por lo tanto, todas las aristas, ángulos
diedros y ángulos poliedros serán iguales.
Sólo existen cinco poliedros regulares y
son: Nº de caras Cara
Tetraedro Regular 4 Triáng. Equ.
Hexaedro Regular 6 Cuadrados
Octaedro Regular 8 Triáng. Equ.
Dodecaedro Regular 12 Pentágono R.
Icosaedro Regular 20 Triáng. Equ.

4. HEXAEDRO
REGULAR
TETRAEDRO
REGULAR
A
B
C
E
F
G
H
A
B
C
D

5. OCTAEDRO
REGULAR
A
F
C
B
E

6. DODECAEDRO REGULAR

7. ICOSAEDRO REGULAR

8. Un poliedro es una figura tridimensional
formada por regiones poligonales
llamadas caras, a las intersecciones de
estas caras se les denomina aristas y las
intersecciones de las aristas forman los
vértices.
OBSERVACIONOBSERVACION

10. PRISMAPRISMA
Se llama prisma al poliedro limitado por dos
polígonos congruentes y paralelos llamados
bases y por caras laterales que son
paralelogramos

11. Ejemplos:
Prisma
recto
Prisma
recto
Prisma
oblicuo
A B
C
D
E
F G
H
I
J

12. PRISMA
REGULAR:
Un prisma regularprisma regular es un prisma recto cuyasprisma recto cuyas bases
son regiones poligonales regularesregiones poligonales regulares
Ejemplo:

13. AREA LATERAL DE UN PRISMA
RECTO
El área lateral de un prisma recto es igual al
producto del perímetro de la base por la altura.
a
h
a
h
a a a a
Alateral= perímetro x h
Ejemplo:
=

14. AREA TOTAL DE UN
PRISMA
Se obtiene sumando al área lateral las áreas de las
bases
Ejemplo:
a
h
a
h
a a a a
Atotal = Alateral +2Abase
= +

15. VOLUMEN DE UN PRISMA
a
h
a
h
El volumen de un prisma es igual al producto del
área de su base por su altura.
V= Abase x h

16. basebase
PIRÁMIDEPIRÁMIDE
Una pirámidepirámide es un poliedro formado por caras
laterales que son regiones triangularesregiones triangulares que
tienen un vértice comúnvértice común y una región poligonaly una región poligonal
llamadallamada basebase que no contiene al vérticeque no contiene al vértice
Ejemplos:
altura
altura

17. PIRÁMIDE REGULAR:
Apotema(Ap)
Arista lateral (a)
-Las caras lateralescaras laterales son triangulostriangulos isósceles congruentesisósceles congruentes
-Las aristasaristas laterales son congruentes
-El apotemaapotema (Ap)(Ap) es la altura relativa a la arista de la
base de cualquiera de sus caras laterales
altura
V
A
B
C
D
M
H
Apotema de la
base (ab)
Lado de la base (l)

18. AREA
LATERAL
Si “l” es el lado de la base de la pirámide
y Ap la apotema de la pirámide
Ap
l
DE UNA PIRAMIDE
REGULAR
pLAT A
2
nl
A =

19. AREA TOTAL DE
UNA
Ap
+
PIRAMIDE
REGULAR
)a(A
2
ln
A bpTOT +=
ab

20. base
h
VOLUMEN DE UNA PIRÁMIDE
El volumen de una pirámide es igual a un tercio
el producto del área de su base por su altura
V = Abase x h
3

21. Se desea empaquetar pelotitas de ping-pong en
grupos de 4 pelotitas, en cajas con forma de
prismas rectangulares. Si el diámetro de la
pelota es de 4 cm, determine las dimensiones de
la caja mas económica de fabricar.
Ejemplos:

22. Solución:
Analizar las posibles formas

23. Problema:
Se desea fabricar envases para jugo de frutas, con
forma de tetraedro regular y que tengan una
capacidad de 250 cc.
•¿Cuánto debe medir la arista de cada cara
del envase?
•¿Cuántos cm2
de “tetrapak” se empleará en
cada envase?

24. Ejercicios planteados
en el libro

25. Preg 5 pág 66
papel
cuarto

26. Pregunta 7, pág 66
9 . 5 m
2 . 4 m
2 0
c m

27. Pregunta 10, pág 66
3 m
3 m
3 m4 .4 5 m

28. Pregunta 12, pág 66
2 . 4 m
7 2 c m

29. Pregunta 24, pág 71
6 0 c m
6 0 c m
3 0 c m
1 0 c m
⇒