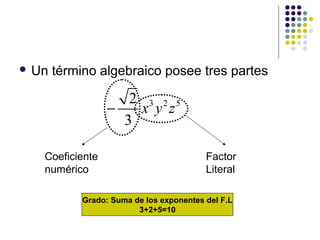
Este documento presenta conceptos básicos de álgebra como expresiones algebraicas, términos algebraicos, clasificación de expresiones, operaciones con expresiones algebraicas como suma, resta, multiplicación y factorización. También introduce traducción entre lenguaje algebraico y lenguaje verbal.

1. ÁLGEBRA y
ECUACIONES
Expresión algebraica
Clasificaciones
Operatoria
Traducción
Regularidades
Ecuaciones

2. Expresiones Algebraicas
 Una expresión algebraica es una
expresión en la que se relacionan valores
indeterminados con constantes y cifras,
todas ellas ligadas por un número finito de
operaciones de suma, resta, producto,
cociente, potencia y raíz.
 Ejemplos
1
2.
)
2)
2)
2
32
2
+
−
+
+
x
xyx
c
xyxb
xyxa
2

3. Una expresión algebraica es toda
combinación de números y letras unidos por
los signos de las operaciones aritméticas.
Los números se llaman coeficientes y las
letras se llaman variables, incógnitas o
indeterminadas.

4. Término algebraico
 Un término algebraico es una expresión
algebraica que no posee símbolos de sumas
o restas.
3 2 52
3
x y z−
3 2 52
3
x y z− +
a b c+ +1

5.  Un término algebraico posee tres partes
3 2 52
3
x y z−
Coeficiente
numérico
Factor
Literal
Grado: Suma de los exponentes del F.L
3+2+5=10

6.  Las letras que representen un valor numérico fijo
son consideradas como parte del coeficiente
numérico y no del factor literal.
 Se dice que dos términos son semejantes cuando
ellos tienen IDENTICO factor literal.
 Esto debe incluir todas las letras con sus
respectivos exponentes.
 En una expresión algebraica se deben reducir los
términos semejantes antes de clasificarla.

7. 1. Reduce los términos semejantes:
Reducción de términos semejantes
a) 5a + 7a + 4a
b) 4x + 5x - 2x + x
c) -12a - 8a + 4a + a
d) 9x - 8y + 5y - 2x
e) 14x - x - 17y + 4x - y + 23x - 16y
f) 7x + 4x2
+ 5x + 9x2
g) 2,5a - 0,4a - 3,6a + 4a
h) -a + 7,1a + 2a - 3,5a
i) 2/3 a + 3/4 b - a - b + 1/6 a - 2/5 b

8. Clasificación
 Las expresiones algebraicas se pueden
clasificar según la cantidad de términos que
poseen o por el grado de sus términos.
Según los términos, la clasificación es:
Monomio: un término
Binomio: dos términos
Trinomio: tres término
Polinomio o multinomio: dos o más términos.
8

9.  Según el grado de sus términos, estas
pueden ser
Constantes: grado 0
Lineales: grado 1
Cuadráticas: grado 2
Cúbicas: grado 3
Cuárticas: grado 4….etc.
9

10. Expresión Algebraica
10
x
y
Si x y y son las medidas de los lados de
un rectángulo, 2x + 2y es la expresión
algebraica que nos da el perímetro del
rectángulo.
Su valor numérico para x = 3 y y = 2 nos
da el perímetro de un rectángulo de esas
dimensiones:
2 . 3 + 2 . 2 = 10
Ejemplo:

11. Operatoria con Ex. Alg.
 Es posible trabajar con las expresiones
algebraicas considerando las mismas
operaciones que con los sistemas
numéricos: sumar y multiplicar.
(también restar y dividir)
 Otra operación es la valorización.

12. Valoración de Expresiones
12

13. Suma de Polinomios
 Para sumar dos polinomios se agrupan los términos
del mismo grado y se suman sus coeficientes.
 Ejemplo: Sumar los siguientes polinomios
P(x) = -2x4
+ 5x3
– 3x + 1
Q(x) = 3x3
– 6x2
– 5x - 2
13

14. Propiedades de la Suma
 Asociativa
 Conmutativa
 Existencia de elemento neutro
 Existencia de elemento opuesto
14

15. Resta de Polinomios
 Para restar el polinomio Q(x) del polinomio P(x) se
debe sumar a P(x) el opuesto de Q(x).
P(x) – Q(x) = P(x) + [ - Q(x) ]
 Ejemplo: Restar los siguientes polinomios
P(x) = -2x4
+ 5x3
– 3x + 1
Q(x) = 3x3
– 6x2
– 5x - 2
15

16. Multiplicación de Polinomios
 Para multiplicar dos polinomios se multiplica cada monomio de
uno de ellos por cada uno de los términos del otro y luego se
suman los términos de igual grado.
 Ejemplo: Multiplicar los siguientes polinomios
P(x) = -2x4
+ 5x3
– 3x + 1
Q(x) = 3x3
– 6x2
– 5x – 2
P(x).Q(x) = P(x) 3x3
+ P(x) (-6x2
) + P(x) (-5x ) + P(x)(-2)
16

17. Propiedades de la
Multiplicación
 Asociativa
 Conmutativa
 Existencia de elemento neutro.
17

18. Uso de Paréntesis
 Si tenemos un signo + o – delante de un
paréntesis, conviene eliminar el paréntesis
multiplicando este signo por cada término
dentro del paréntesis.
18

19. Reducir:
19

20. Ejemplos: Operatoria algebraica
 Una caja con fondo cuadrado está hecha
de una pieza cuadrada de cartón de 12
pulgadas de lado. Se cortan cuadrados de
lado x en las esquinas, y los lados se
doblan hacia arriba. Expresar el volumen
y el área superficial de la caja en términos
de un polinomio.
20

21. Resuelve los paréntesis y luego reduce los términos semejantes:
a) (9a - 4b) + (3a - 2b)
b) (-3a + b) - (2a - b)
c) -(x - 3y + 5z) - (4x + 3y - 8z)
d) 4x - (x2
+ 5x - 7) + 6 - (-4 + 3x2
)
e) [9a - (3a + 7) + (6 + 4a)] - (a + b)
f) -[8 + (2x - 1)] + [-(6x - 5) - 2]
g) 7x + {-4x + [(-6 + 5x) - (2x -4)] - 8x}
h) 0,6a - [(1,2 + 0,4b) + (-a + 3,6)] - (-2,2 - 6,2b)
Ejercicios

22. Ejercicios
Eliminar los términos semejantes en los siguientes polinomios:
 8x -3x+7x=
 3x +9y –2x –6y=
 7a2
– 15b3
+ 5b3
+ 9a 2
– 4b3
=
 3a+ 4c + 9c – 7b – 7a- 15c =
 0,01 b2
c – 0,2 c2
b - 0,8 c2
b + 0,99 b2
c=
22

23. Ejercicios
*Eliminar paréntesis y reducir términos semejantes en los siguientes
polinomios
a) (10b +4) +(6 –9b) –(3b-7)=
b) 20 + (-7 +2x) –(-3x-7)=
* Dados los polinomios
A: 2b2
c –3b + 6c B: 4b - c2
b + 12 b2
c C: 4 – 2c
Ejecute las siguientes operaciones:
a) A + B= b) A – C= c) B - A=
23

24. Ejercicios
8. Calcular el perímetro de la siguiente figura:
x +y
2x +y x
3x +y –3
9. El perímetro de un rectángulo es 8x –6 y un lado es 3x +7
¿Cuánto mide el otro lado?
24

25. Productos Notables
25

26. Ejercicio
 Escribir los desarrollos de
2
43
232
2
3
1
3
2
)
)()
)32()






−−
−
+
xxc
xxb
xa
3
23
34
3
3
2
2
1
)
)()
)32()






+−
+−
+−
xxf
xxe
xd
26

27. Ejemplo aplicación productos notables
 1. Se tiene un cubo cuya arista mide x
metros. Si se necesita disminuir el
volumen, sacando y metros de la arista,
exprese el nuevo volumen del cubo.
 2. Se tienen x bolsas de suero que
contienen y ml, si la cantidad de bolsas
aumenta en 5 y el contenido disminuye en
30ml, exprese la nueva cantidad total de
suero.
27

28. Factorización
Factorización:
FACTOR: Expresión algebraica que multiplica a una segunda expresión
( )( )zxba −− ( ) ( )zxba −− y
Sonfactores
( )zxba −− ( )zxb −y
Operación necesaria para re-escribir una expresión
algebraica como producto de factores
))((22
babammbma −+=−

29. Factorización
29

30. Ejemplo Máx.
factor
común
Segundo
factor
Factorización
Caso I. Factor Común
Resolviendo los ejemplos:
22
mbma −
xyx −2
3
4222
3624 yxxya −
)1()1( +−+ xbxa
m 22
ba − )( 22
bam −
)13( −xyx
)32(12 222
xyaxy −
))(1( bax −+

31. nmmnm 8463 2
−+−
Caso Ib. Factor Común por
Agrupación de Términos
Resolviendo los ejemplos:
)84()63( 2
nmmnm −+−
)2(4)2(3 nmnmm −+−)2)(43( nmm −+

32. Caso II. Factorización de
Trinomios
Trinomio Cuadrado Perfecto
22
2 baba ++
• Determinar si es tcp
• Obtener la raíz cuadrada
del primer y tercer
términos
• Observar el signo del
segundo término
• Escribir el binomio al
cuadrado
122
+− xx
9124 22
+− axxa

33. Caso III. Factorización de la
Diferencia de Cuadrados
12
−a • Identificar la diferencia
de cuadrados
• Obtener la raíz cuadrada
del primer y segundo
términos
• Escribir el producto de
binomios conjugados
6
169 x−
22
12 yxx −++
22
ba −

34. Ejercicio: La expresión x2
- a2
es una diferencia de cuadrados.
Escribir las siguientes diferencias como producto de
binomios.
64)
4)
36
1
)
100)
8
4
2
2
−
−
−
−
xd
xc
xb
xa
34

35. La diferencia entre el
doble de x y su mitad.
2x –
Dos veces el producto de m
y n. 2mn
Un tercio de x.
Tres veces la suma de f
y g.
3(f + g)
El triple de a. 3a1.
2.
3.
4.
5. x
2
x
3
Traducción:
Matemática-Español
Español lenguaje algebraico

36. Ejemplo aplicación
Escribir en notación algebraica las siguientes
Situaciones:
1. El volumen (V) de un cono es igual a un tercio
del producto de área basal por su altura (h). El
área basal es π veces el cuadrado de su radio
(r).
2. Si a es la edad actual de Homero, expresar en
lenguaje algebraico:
i. La de edad de Homero dentro de 10 años.
ii. La edad que tenía Homero hace 5 años.
iii. El triple de la edad de Homero.
36

37.
Enuncia verbalmente las siguientes expresiones
algebraicas:
1. x - 2 : "La diferencia entre un número y 2"
2. 2x
3. x + 3
4. 2x + 5
5. 2x3
6. x - 3y
7. x2
8. 5x
9. x + y
10. 2x - 4y
Lenguaje algebraico a lenguaje
verbal

38. Lenguaje verbal a lenguaje
algebraico
 1. Un número cualquiera.
 2. El doble de un número cualquiera.
 3. Un número aumentado en 5.
 4. Un número disminuido en 3.
 5. Un número aumentado en su mitad.
 6. El antecesor de un número cualquiera.
 7. El sucesor de un número cualquiera.
 8. Un número par cualquiera.
 9. Un número impar cualquiera.
 10. Dos pares consecutivos cualesquiera.

39.  11. Tres impares consecutivos cualesquiera.
 12. El exceso de un número sobre 3.
 13. El exceso de un número cualquiera sobre otro
número cualquiera.
 14. La quinta parte de un número.
 15. La centésima parte de un número.
 16. Las tres cuartas partes de un número
cualquiera.
 17. El cuadrado de un número cualquiera.
 18. El cubo de un número cualquiera.
 19. El doble de un número aumentado en 4.
 20. El triple de un número disminuido en 5.

40. Regularidades Numéricas:
 Considere la siguiente secuencia numérica
2, 4, 6, 8, 10, 12,…
¿cuáles son los siguientes dos términos?
 Y en la siguiente secuencia:
-4, 7, -10, 13, -16, 19….
O en
2, 3, 5, 7, 11, 13….

41.  Muchas veces se dificulta el “encontrar la
fórmula” que determina los siguientes
términos.
 Las anteriores son: 2n ; ; no hay
 Otros ejemplos interesantes son los
geométricos
( 1) (3 1)n
n− +

42.  ¿Cuántos triángulos habrán en las siguientes
“piramides”?
 En general se busca la relación entre el
número de la figura y el número
correspondiente.

43.  Figura: Número
1 1
2 4
3 9
n n*n

44. Ecuaciones
Una Ecuación es una igualdad con una o más
cantidades desconocidas llamadas incógnitas.
Resolver una ecuación es encontrar el valor de la o
las incógnitas que hacen verdadera la igualdad.
Ejemplos: • x + 17 = 23
• 3 x = 6
• x + y = 2 + 4y

45. Una ecuación puede ser representada por una balanza
que se encuentra en equilibrio.
Lo que está en el platillo de la izquierda pesa lo mismo
que el platillo de la derecha.
x + 4 = 8 + 4

46. •Al sumar o restar un mismo número a ambos
miembros de una igualdad, esta se mantiene.
•Si se multiplican o dividen por un mismo número
(distinto de cero) ambos miembros de la igualdad, esta
se mantiene.
•Las ecuaciones de las formas
a + x = b (ecuaciones aditivas) y
a · x = b (ecuaciones multiplicativas)
Se denominan de Primer Grado, porque el exponente
máximo de la incógnita es 1.

47. 2
32
64-
64 32
485216325
216483255
−=
=
−=
−+−=+−+
−−=++−
x
x
x
xxxx
xxxx

48. Resolviendo problemas
Pedro y Cecilia tienen entre los dos 57 láminas y Cecilia tiene 11 más
que Pedro, ¿cuántas láminas tiene cada uno?
Ana María decide salir a correr todas las mañanas y se desafía a sí
misma a aumentar su recorrido en 1/2 km, por día. Sumando lo
recorrido cada día, al cabo de 9 días el recorrido acumulado es
igual a 58,5 km, ¿cuánto corrió el décimo día?
Crea un problema, que represente a la ecuación siguiente:
 a) x + 12 = 23
 b) x + x + 24 = 53
 c) x + x - 56 = 123
 d) 2x + 5 =34
 e) x + 5600 = 10000
 f) 300 - x = 770.