Semana01 ord-2013-i

UNMSM – CENTRO PREUNIVERSITARIO Ciclo 2013-I
Solucionario_Semana Nº 1 (Prohibida su reproducción y venta) Pág.1
UNIVERSIDAD NACIONAL MAYOR DE SAN MARCOS
Universidad del Perú, DECANA DE AMERICA
CENTRO PREUNIVERSITARIO
SOLUCIONARIO GENERAL
Habilidad Lógico Matemática
EJERCICIOS DE CLASE Nº 1
1. Iván tiene cuatro frascos herméticamente cerrados y no transparentes, dos azules y
dos rojos, los cuales contienen mermelada de uno de los siguientes sabores: fresa,
piña, naranja y pera. Es verdad que:
I. Las mermeladas de fresa y naranja se encuentran en frascos de colores
diferentes.
II. Si la mermelada de fresa está en un frasco rojo, entonces la mermelada de piña
y pera están en frascos del mismo color.
Luego, es cierto que:
A) La mermelada de piña está en un frasco de color azul.
B) Las mermeladas de pera y naranja se encuentran en frascos del mismo color.
C) Un frasco azul contiene mermelada de pera.
D) Los frascos de color rojo no contienen mermelada de naranja.
E) La mermelada de fresa se encuentra en el frasco de color azul.
Solución:
1) De (I): Las mermeladas de piña y pera también se encuentran en frascos
diferentes.
2) De (II) y (1): La mermelada de fresa no puede estar en un frasco rojo, luego se
encuentra en un frasco azul y la mermelada de naranja en un frasco de color
rojo.
Clave: E
2. Danielito tiene dos cubos de madera, uno de ellos tiene impreso, en cada una de
sus caras, una letra y en el otro cubo, en cada cara, un número, como se indica en
la figura. Danielito ha colocado en una mesa ambos cubos, como se indica en la
figura. En las caras en contacto, ¿qué letra y qué número están impresos?
A) C y 1 B) A y 2 C) C y 2 D) A y 1 E) E y 2
Marcos Elantiguo

Solución:
1) De las figuras se obtienen los siguientes desarrollos de ambos cubos.
2) Luego, en las caras en contacto están impresos la letra C y el número 1.
Clave: A
3. Ana, Betty y Carla llevan a todos sus hijos al cine. Los nombres de los niños son
Raúl, Beatriz, Ángela, Mónica y Jesús. Se sabe que:
I) A Raúl y al hijo único de Betty le gustan las películas de terror.
II) Las hijas de Carla y la hermana de Raúl prefieren las películas de acción.
III) Carla y la madre de Mónica prefieren que sus hijos vean una película de ciencia
ficción.
Entonces, es falso afirmar que:
A) Jesús es hijo de Betty. B) Raúl es hermano de Ángela.
C) Mónica y Raúl son hermanos. D) Ana no es la madre de Beatriz.
E) La madre de Beatriz no es Betty.
Solución:
1) De (I): El hijo de Betty es Jesús.
2) De (II): Raúl es hijo de Ana.
3) De (III): Ángela y Beatriz son hijas de Carla, y Raúl y Mónica son hermanos.
Clave: B
4. En la figura se muestran tres discos sobre una mesa en cuyas caras opuestas están
impresos los números 3, 6 y 5, uno en cada disco. Si se arrojan los tres discos sobre
la mesa se puede obtener como suma, de los tres números que se pueden ver, los
ocho números diferentes desde 7 hasta 14. Tal cuál están ubicados los discos en la
figura, de izquierda a derecha, ¿cuál es una posible secuencia de los números que
no se pueden observar?
A) 5-6-3 B) 3-6-5 C) 5-3-6 D) 6-5-3 E) 6-3-5
Marcos Elantiguo

Solución:
1) De los posibles valores en la suma de los tres números que van las caras
visibles se puede ver que las posibles distribuciones son
Clave: A
5. Un juego tiene las siguientes reglas: dos jugadores toman por turnos una, dos o tres
cartas de un mazo que inicialmente tiene 20. El jugador que toma la última carta
pierde. Lucía y Andrea deciden jugar una partida. Si Lucía pretende asegurarse
ganar la partida, entonces
A) debe dejar empezar el juego a Andrea y luego retirar una carta.
B) debe iniciar el juego retirando dos cartas.
C) debe iniciar el juego retirando una carta.
D) debe iniciar el juego retirando tres cartas
E) debe dejar empezar el juego a Andrea y luego retirar dos cartas.
Solución:
1) Debe iniciar el juego retirando tres cartas, de este modo jugando
apropiadamente se puede asegurar de retirar la carta décimo primera y la
décimo quinta. Luego quedan cinco cartas y el turno es de Andrea, sea cual
sea la cantidad de cartas que recoja en esta oportunidad, si Lucía juega con
criterio, Andrea se verá obligada a retirar la última carta.
Clave: D
6. Cinco varones y cinco mujeres se reunieron para jugar ping-pong. Los partidos se
desarrollaron en dos rondas, en donde cada mujer jugó dos partidos y en cada una
de ellos enfrentó a un hombre diferente. Los partidos de ambas rondas se realizaron
simultáneamente. Se observó que
– Jenny y Juanita tuvieron los mismos rivales.
– Patricia enfrentó en su segundo partido al que Sandra enfrentó en su primer
partido
– Patricia no jugó con Andrés, y Camila no jugó con Tomás. Juan ganó un partido.
– Camila y Sandra no jugaron con Santiago.
– Sandra jugó su segundo partido con el que jugó Camila en su primer partido.
– El segundo partido de Juanita fue con Miguel.
¿Con quién jugó Juan en su primer y segundo partido respectivamente?
A) Camila - Sandra B) Patricia - Camila C) Sandra – Patricia
D) Juanita - Jenny E) Patricia - Sandra
Marcos Elantiguo

Solución:
1) Camila jugó su primer partido con Andrés o Juan.
2) Patricia jugó su segundo partido con Juan o Tomás.
3) Sandra jugó su primer partido con Juan o Tomás.
Luego
Primer partido
Camila – Andrés
Jenny – Miguel
Patricia – Juan
Juanita – Santiago
Sandra – Tomás
Segundo partido
Juanita – Miguel
Jenny – Santiago
Camila – Juan
Patricia – Tomás
Sandra – Andrés
Clave: B
7. Rebeca vive en el mismo edificio que yo, pero no sé en qué departamento. Le
pregunté a cuatro de mis vecinos por el número de su departamento, y ellos afirman:
– Vecino 1: El número de su departamento es el 9.
– Vecino 2: El número de su departamento es primo.
– Vecino 3: El número de su departamento es par.
– Vecino 4: El número de su departamento es 15.
El portero no quiso decirme en qué departamento vive Rebeca, pero me aseguró que
exactamente dos de las afirmaciones anteriores son falsas.
¿En qué departamento vive Rebeca?
A) 1 B) 15 C) 3 D) 9 E) 2
Solución:
1) Dos de los vecinos 1, 3 y 4 tienen que estar mintiendo, luego el vecino 3 está
diciendo la verdad y el número buscado es par.
2) Así los vecinos 1 y 4 están mintiendo, luego el vecino 2 dice la verdad. Luego el
departamento de Rebeca debe ser el 2.
Clave: E
Marcos Elantiguo

8. En cada uno de los círculos de la figura se debe escribir uno de los dígitos 1, 2, 3
o 4. En cada fila y columna no debe repetirse los números. En cada conjunto de
cuatro círculos unidos entre sí por un segmento, no debe repetirse los números.
Halle la suma de los dígitos que se ubican en los círculos sombreados.
A) 5 B) 7 C) 4 D) 3 E) 6
Solución:
1) En la figura se indica la distribución de los números.
2) Suma pedida es 5.
Clave: A
9. De un grupo de 277 personas, 100 hablan francés, 130 inglés y 119 italiano; 80 solo
hablan francés, 60 solo inglés, 50 solo italiano y 72 hablan por lo menos 2 idiomas.
¿Cuántas personas no hablan ninguno de los tres idiomas?
A) 5 B) 10 C) 25 D) 15 E) 20
Solución:
1) # personas que no hablan ninguno de los tres idiomas: x
x 277 (80 60 50 72)
x 15
     
 
Clave: D
10. Se tiene un conjunto de 420 personas que ven los canales de televisión A, B y C.
Resulta que: 240 no ven el canal A, 180 no ven el canal B, 150 no ven el canal C. Si
los que vieron por lo menos dos canales son 230 personas, ¿cuántas personas ven
los tres canales?
A) 10 B) 20 C) 40 D) 60 E) 80
Marcos Elantiguo

Solución:
1) # personas que ven solo un canal = 420 – 230 = 190.
2) # personas que ven solo dos canales = (240 + 180 + 150) – 2 x 190 = 190.
3) # personas que ven tres canales = 230 – 190 = 40.
Clave: C
11. Aldo, Giovanni y Giacomo han decidido regalar a Nicolás, por su cumpleaños, el
videojuego que desea desde hace tiempo. Sin embargo, ninguno de ellos tiene el
dinero suficiente para comprar el videojuego: a Aldo le faltan 17 soles, a Giovanni 13
soles y a Giacomo 21 soles. Ellos deciden juntar sus ahorros y descubren así que,
no solo pueden regalar el videojuego a su amigo, sino que también pueden
comprarse otro igual y tener todavía un sobrante de 7 soles. ¿Cuánto cuesta el
videojuego?
A) S/. 48 B) S/. 58 C) S/. 72 D) S/. 64 E) S/.98
Solución:
1) Precio del videojuego: S/. x.
2)
Aldo : x 17
Giovanni : x 13
Giacomo : x 21
 


 
Luego:
(x 17)(x 13)(x 21) 2x 7
x 58
      

Clave: B
12. De dos aleaciones con diferente porcentaje de cobre que pesan 15 kg y 10 kg se
cortan dos pedazos de igual peso. El pedazo cortado de la primera aleación se funde
con el resto de la segunda y el pedazo cortado de la segunda aleación se funde con
el resto de la primera, después de lo cual el porcentaje de cobre en ambas
aleaciones es la misma. ¿Cuánto pesa cada uno de los pedazos cortados?
A) 4 kg B) 7 kg C) 2 kg D) 3,5 kg E) 6 kg
Solución:
1) % cobre 1º aleación y segunda aleación: a% y b%.
2) Peso de uno de los pedazos cortados: x kg
Entonces:
ax b(15 x) a(10 x) bx
100 100 100 100
15 10
x 6
 
 


Clave: E
Marcos Elantiguo

13. En la figura se indica un lago en el que hay
seis islas las cuales están interconectadas,
entre sí y con el exterior del lago, mediante
puentes. De las siguientes afirmaciones
indicar cuales son verdaderas.
I. Si se desea dar un paseo por todos
los puentes es necesario repetir por lo
menos uno de ellos.
II. Si se inicia el recorrido en F, se puede
recorrer todos los puentes sin
necesidad de repetirlos.
III. Si se inicia y se finaliza el recorrido en el exterior del lago con el propósito de
recorrer todos los puentes, entonces por lo menos se debe repetir dos puentes.
A) Solo I B) Solo II C) Solo III D) II y III E) I y II
Solución:
1) Se T un punto del exterior del lago,
entonces en la figura se indica un
esquema de los puentes y las islas.
2) Esta red solo tiene dos vértices impares,
luego para recorrerla completamente no
es necesario repetir puentes.
3) Si el recorrido se inicia en el punto,
entonces no es necesario repetir
puentes.
4) Si el inicio y fin del recorrido es el punto
T, entonces será necesario repetir por lo
menos dos puentes.
Clave: D
14. En la figura se indica un armazón hecho de alambre, dos cubos con cuatro aristas
comunes. Si una hormiga recorre por todas estas aristas, ¿cuál es la longitud mínima
de su recorrido?
A) 2,3 m
B) 2 m
C) 2,4 m
D) 2,2 m
E) 2,1 m
Marcos Elantiguo

Solución:
1) Longitud de la red: 20x10 = 200 cm
2) Longitud de repeticiones = 3x10 = 30 cm
Long mín recorr = 200 + 30 = 230 cm = 2,3 m
Clave: A
EJERCICIOS DE EVALUACIÓN Nº 1
1. Sofía tiene en su pecera seis peces: dos azules, 2 amarillos y dos rojos; sus
longitudes son: 3 cm, 6, 6, 9, 9 y 12 cm. Ella ha observado que
– Peces del mismo color tienen longitudes diferentes.
– El pez más largo es amarillo.
– El pez más corto no es rojo.
– Un pez azul es 6 cm más largo que el otro azul.
Entonces es cierto que:
I. La diferencia de longitudes de los peces rojos es 3 cm.
II. Los dos peces azules juntos miden lo mismo que uno de los peces amarillos.
III. Los dos peces amarillos juntos miden lo mismo que un azul y un rojo juntos.
A) I, II y III B) Solo II C) I y III D) Solo I E) Solo III
Solución:
1) En el gráfico se tiene el esquema:
Clave: A
Marcos Elantiguo

2. En una reunión se encuentran Luz, Elena, Magali y Sofía cuyas profesiones son
bióloga, arquitecta, ingeniera y psicóloga, aunque no necesariamente en ese orden. Si
se sabe que:
 Luz no simpatiza con la arquitecta,
 Magali es amiga de la bióloga y de la psicóloga,
 Elena no es ingeniera y no simpatiza con Magali.
¿Cuáles de las siguientes afirmaciones son verdaderas?
I) Elena es psicóloga
II) Sofía es ingeniera
III) Magali es ingeniera
A) Solo II B) II y III C) Solo III D) I y III E) Solo I
Solución:
1) Elena no es ingeniera, ni bióloga ni psicóloga, luego es arquitecta.
2) Magali no es bióloga ni psicóloga ni arquitecta, luego es ingeniera.
Clave: C
3. Después de tres partidos de un torneo de futbol, el equipo Hijos del Sol ha anotado
3 goles y ha recibido 1. En el torneo se dan 3 puntos por partido ganado, 1 punto por
partido empatado y 0 puntos por partido perdido. ¿Cuál de las siguientes
puntuaciones no puede ser la que tiene dicho equipo en este momento?
A) 7 puntos B) 6 puntos C) 5 puntos D) 4 puntos E) 3 puntos
Solución:
1) La única forma de obtener 3 puntos con 3 partidos es habiéndolos empatados
todos o habiendo perdido dos de ellos, lo cual es imposible con los datos del
problema.
Clave: E
4. En un baúl hay 5 cofres, en cada cofre hay 3 cajas, y en cada caja hay 10 monedas
de oro. El baúl, los cofres y las cajas están cerrados con llave. ¿Cuál es la menor
cantidad de cerraduras que hay que abrir para obtener 50 monedas?
A) 10 B) 8 C) 6 D) 5 E) 3
Solución:
1) Hay que abrir 5 cajas, que están contenidas en al menos 2 cofres, que están
dentro del baúl.
Por lo tanto, hay que abrir 8 cerraduras como mínimo.
Clave: E
Marcos Elantiguo

5. De una muestra recogida de 200 transeúntes se determinó lo siguiente: 60 eran
mudos, 70 eran cantantes callejeros y 90 eran ciegos, de estos últimos, 20 eran
mudos y 30 eran cantantes callejeros. ¿Cuántos de los que no son cantantes
callejeros no eran mudos ni ciegos?
A) 30 B) 35 C) 40 D) 45 E) 60
Solución:
1) Con los datos del problema se construye el siguiente diagrama
2) Los que no son cantantes, ni mudos, ni ciegos son 30.
Clave: A
6. En el departamento de control de calidad de la fábrica de micro chips se consideran
tres defectos A, B y C como las más importantes. Se eligen al azar 200 productos y
se observan que:
– 58 presentan el defecto A.
– 72 presentan el defecto B.
– 80 presentan el defecto C.
– 100 productos presentan exactamente un defecto.
– 10 productos presentan los tres defectos.
¿Cuántos productos presentan al menos un defecto?
A) 100 B) 130 C) 140 D) 150 E) 160
Solución:
1) 100 58 72 80 10
# soloundefecto 2#dosdefectos #def A #defB #def C 3# tresdef
#dosdef 40
 
     


 
2)
#almenosundef #undef #dosdef #tresdef
#almenosundef 100 40 10 150
   

    
Clave: D
Marcos Elantiguo

7. A Jacinto le prometieron pagar por un año de trabajo S/. 2 100 más una refrigeradora
y dos licuadoras. Si luego de seis meses de trabajo es despedido y recibe como
pago S/. 1 500 más una licuadora, ¿cuánto cuesta la refrigeradora?
A) S/. 900 B) S/. 850 C) S/. 1 250 D) S/. 1 100 E) S/. 600
Solución:
1) Pago por un año: 2100 + refrig +2 licuadoras
2) Pago por 6 meses será la mitad de lo anterior, pero por dato esto equivale a
S/. 1500 mas una licuadora.
3) Luego la mitad del valor de una refrigeradora es 1500-1050=450
Por lo tanto, la refrigeradora cuesta S/. 900.
Clave: A
8. Raquel tiene un canasto con cierta cantidad de manzanas, las cuales desea repartir
a sus tres hermanas. A la primera le da la mitad de las manzanas y una manzana
más. A la segunda la mitad de lo que quedó y una manzana más y para la tercera la
mitad de lo que quedó y tres manzanas más, con lo que el canasto quedó vacío.
¿Cuántas manzanas contenía el canasto inicialmente?
A) 45 B) 38 C) 44 D) 24 E) 30
Solución
1) # manzanas=x
1 x x 1 1 x x 3
1 1 quedan :
1ºrecibi
x x
1 q
1 1
2 2 4 2 2
uedan : 1
1 x 3 1 x 3
3 queda
ó :
2ºr
2 4
n : 3
2 4 2 2
ecibió :
3ºrecibió :
4 2
2 2
2
   
          
  
   
      




 
  




 


Luego:
1 x 3
3 0
2 4 2
x 30
 
    
 

Clave: E
9. Se desea dibujar la cuadrícula de un tablero de ajedrez cuyos escaques sean
cuadrados de 1 cm de lado. Si dicho dibujo se debe hacer de un solo trazó continuo
sin separar la punta del lápiz del papel, ¿cuál es la longitud mínima que debe
recorrer la punta del lápiz?
A) 160 cm B) 156 cm C) 144 cm D) 148 cm E) 158 cm
Marcos Elantiguo

Solución:
1) En la figura se indican los tramos que se deben repetir
2) Long de la red = 18 x 8 = 144 cm
3) Long trazos rep =14 cm
Long min = 158 cm
Clave: E
10. La malla de alambre que se muestra en la figura está construida por segmentos,
mutuamente perpendiculares, de alambre de 10 cm de longitud. Si una hormiga
recorre toda la malla, ¿cuál será la longitud mínima de su recorrido?
A) 270 cm
B) 240 cm
C) 260 cm
D) 300 cm
E) 280 cm
Solución:
1) Longitud de la malla = 24 x 10 = 240 cm
2) Longitud de repeticiones = 3 x 10 = 30 cm
3) Long min recorrido = 270 cm.
Clave: A
Marcos Elantiguo

Habilidad Verbal
SEMANA 1 A
LA JERARQUÍA TEXTUAL: EL TEMA CENTRAL
El texto es una cadena de enunciados, pero no todos gozan del mismo estatus. En
todo texto, hay un principio de jerarquía. Este principio sostiene que el texto está
gobernado por una noción capital (el tema central), crucial para entender la trama textual,
puesto que es el concepto de mayor prominencia cognitiva en la estructura semántica del
conjunto de enunciados. El tema central se formula mediante un vocablo o una frase
nominal: Por ejemplo, «La importancia del sueño».
ACTIVIDADES DE RECONOCIMIENTO DEL TEMA CENTRAL
Formule el tema central del siguiente texto.
TEXTO A
La ciencia podría lograr en breve lo que parecía imposible: procrear un ser humano
sin la necesidad de una pareja hombre-mujer. El doctor Calum Mackellar, profesor en
bioética y bioquímica de la Universidad de Edimburgo, sostiene que es posible la
concepción de hijos por parte de parejas homosexuales, en este caso de varones, y que
solo precisarían un «vientre de alquiler» femenino. Si bien otros científicos cuestionan la
viabilidad del procedimiento sugerido, ya que los embriones de los mamíferos precisan de
los genes maternos para desarrollarse con normalidad, el debate una vez más se centra
en los aspectos éticos y morales.
¿Sería la homoconcepción una opción válida para la sociedad? ¿Podría un núcleo
familiar prescindir hasta genéticamente de un sexo?
Tema central: ……………………………………………………………………..
SOLUCIÓN: La homoconcepción o forma polémica de procreación
Lea el texto y conteste la pregunta de opción múltiple.
TEXTO B
Un nuevo estudio demuestra que los perros tienen un sistema de comunicación de
gran complejidad. Los ladridos de tu perro, más allá de causarte problemas con vecinos y
no dejarte dormir, están cargados de significados que los canes, y a veces los humanos,
pueden decodificar. Brian Hare y Vanessa Woods, investigadores de la Universidad de
Duke, convencidos de la inteligencia canina, condujeron varios experimentos en los que
comprueban que existe entre los perros un elaborado lenguaje. Al igual que los humanos,
los perros pueden vocalizar. Si bien no lo hacen con la misma sofisticación, la movilidad
de sus cuerdas vocales les permite alterar su voz para producir diferentes sonidos con
diferentes significados. Los ladridos y gruñidos varían según el contexto.
En una prueba, los científicos grabaron a dos perros gruñendo: uno mientras
protegía su comida y otro al acercársele un desconocido. En una segunda etapa, se
colocó un hueso jugoso y cada vez que un perro iba hacia él se reproducían las
grabaciones. Los perros titubeaban al escuchar el gruñido ocasionado por el afán de
proteger la comida más que el emitido cuando el perro presenciaba a un extraño.
Marcos Elantiguo

En un experimento similar, se grabó el ladrido de un perro al sentirse solo y otro
cuando se aproximaba un extraño. Diferentes perros escucharon las grabaciones y se
ponían en alerta al oír el ladrido provocado por un extraño. Claramente, los perros podían
distinguir entre los diferentes sonidos y comprender sus significados. A pesar de
acompañarnos durante miles de años, realmente sabemos poco acerca del lenguaje
canino, quizá estudios como éste nos ayuden a entender mejor a nuestro mejor amigo.
1. ¿Cuál es el tema central del texto?
A) Los extraños significados que subyacen a los ladridos de los perros
B) El complejo sistema de comunicación canino a la luz de un estudio *
C) Las grabaciones de los gruñidos canidos decodificados por perros
D) La vocalización en perros y su equivalencia con el lenguaje humano
E) La necesidad de gruñir que los perros evidencian al sentir hambre
SOLUCIÓN: B. El texto desarrolla la compleja forma de comunicación de los perros
basada sustancialmente en ladridos y gruñidos; esta ha sido develada gracias a un
estudio experimental en el que se usaron grabaciones de gruñidos como estímulos.
LA JERARQUÍA TEXTUAL: LA IDEA PRINCIPAL
Una vez que hemos identificado el tema central de un texto, podemos determinar la
idea principal. Esta se formula mediante una oración o un enunciado. Por ejemplo, si el
tema central de un texto es «La importancia del sueño», la idea principal puede ser «El
sueño es importante porque cumple con una función esencial de equilibrio de la vida
mental». En consecuencia, la idea principal es el desarrollo esencial del tema central que
se hace en el texto.
ACTIVIDADES DE RECONOCIMIENTO DE LA IDEA PRINCIPAL
A. Formule la idea principal del siguiente texto.
TEXTO A
Todos los mamíferos producen lágrimas, humedecen el ojo y lo mantienen libre de
infecciones. Sin embargo, únicamente las personas podemos llorar. Las lágrimas
motivadas por la emoción son un rasgo exclusivamente humano. ¿Qué sucede en nuestra
estructura cerebral que posibilita el llanto y nos diferencia del resto de los animales? De
acuerdo al profesor inglés Michael Trimble del Instituto de Neurología en Londres, la
evolución y la cultura moldearon la mente humana para que pudiera expresar sus
sentimientos a un nivel superior al resto del reino animal. Las lágrimas emotivas o
aquellas producidas por una experiencia estética no se encuentran en ningún otro ser
vivo. Según Trimble, el llanto pudo haber sido una de las primeras formas de
comunicación del hombre, antes incluso de que existiera el lenguaje. El poder demostrar
tristeza, alegría, compasión y empatía va de la mano con la realización del ser, con la
teoría de la mente (capacidad de atribuir pensamientos e intenciones a otras personas), y
el percatarse de la finitud de la existencia. Las emociones humanas surgen a partir de una
red compleja de regiones cerebrales interconectadas. Nuestro sistema límbico cerebral
(asociado a las emociones) está relacionado con el sistema nervioso autónomo; como
consecuencia, nuestros sentimientos integran nuestro entorno y nuestras respuestas
corpóreas. El ritmo cardiaco, la respiración y las cuerdas vocales intervienen en el llanto.
Marcos Elantiguo

Es posible que el consuelo que sentimos después de llorar se deba a que se
estimulan los nervios craneales, que a su vez alivian la amígdala cerebral sobreestimulada
por una emoción específica.
Diferentes formas de arte también nos hacen llorar. Una novela, una película, una
obra de teatro y especialmente la música nos conmueve a las lágrimas. Durante un
estudio, se demostró que el 85% de los participantes lagrimaron al escuchar música
emotiva. Estimulando nuestro sistema límbico, la música evoca memorias y sentimientos.
Llorar, por lo tanto, no indica debilidad, sino una cultura y moralidad característicamente
humana. Millones de años de evolución se reflejan en cada lágrima.
Idea principal: …………………………………………………………………………………….
SOLUCIÓN: El llanto es un rasgo cultural privativamente humano producido por millones
de años de evolución, e involucra procesos cerebrales complejos.
B. Lea los siguientes textos y conteste las preguntas de opción múltiple.
TEXTO 1
El hambre, al que deben enfrentarse cada día 870 millones de personas, no es una
fatalidad a la que una parte de la humanidad esté predestinada. Es resultado de la
injusticia; de la violación del derecho fundamental de toda persona a disponer, en todo
momento, de alimentos en cantidad y calidad suficiente que le permitan vivir una vida
digna y saludable.
En un mundo donde la producción agrícola mundial podría ser suficiente para
alimentar al doble de la población mundial, la cifra de personas que pasan hambre se ha
incrementado en más de 1000 millones durante los últimos 3 años.
El alza de los precios de los alimentos en el mercado internacional ha sido la
principal causa de este incremento, pero las causas que provocan el hambre son
numerosas y complejas: políticas comerciales injustas, pobreza, falta de acceso a agua
potable, situación de discriminación de la mujer, desastres naturales, violencia y conflictos
armados, o pandemias son algunas de ellas.
1. ¿Cuál es la idea principal del texto?
A) Es evidente que existe una violación del derecho fundamental a disponer de una
vida digna.
B) Los desastres naturales refuerzan la concepción del hambre como una fatalidad
predestinada.
C) La producción agrícola mundial es suficiente para acabar con el hambre creciente
en el mundo.
D) El hambre que padecen millones de personas deviene de causales diversas y
complejas.*
E) El alza de precios de los alimentos básicos es la causa excluyente del hambre en
el mundo.
SOLUCIÓN: D. El texto sostiene que el hambre creciente en el mundo es producida por
causas de diverso cariz y complejidad, entre las que se cuentan aquellas que son
producto del hombre (alza de precios, guerras, exclusión, etc.), además de desastres
naturales.
Marcos Elantiguo

TEXTO 2
Después de vivir encerrados en un laboratorio, siendo partícipes de múltiples
experimentos médicos, los chimpancés no pueden regresar a una vida normal una vez
dados de alta. La mayoría sufren de depresión y traumatismo y son incapaces de
relacionarse con los demás miembros de su especie. Debido a que compartimos el 99%
de nuestro ADN con los chimpancés, estos animales sirven como ideales modelos de
humanos en la investigación médica. Su similitud genética significa que pueden contraer
casi todas las enfermedades que afectan a las personas hoy en día. Han sido utilizados
principalmente en la elaboración de vacunas y tratamientos como la de hepatitis A, B y el
SIDA.
Alrededor de mil chimpancés se encuentran actualmente en laboratorios, tanto
privados como gubernamentales, tan solo en Estados Unidos. Una vez servida su
sentencia, la mayoría son liberados en santuarios. Muchos de ellos, tras 10 o 15 años de
encierro. Solitarios, apáticos y con varios trastornos mentales, no pueden desarrollar una
vida social sana. Afortunadamente para los chimpancés, un nuevo estudio apunta hacia
los antidepresivos como una posible solución a la vida tras el laboratorio. Godelieve
Kranendonk del Centro de Rescate para Animales Exóticos y Martin Bruene, psiquiatra de
la Universidad de Bochum en Alemania, han administrado a cinco chimpancés dosis de
SSRI (inhibidores selectivos de recaptación de serotonina) con excelentes resultados.
Después de 6 a 8 semanas, los chimpancés recobraron su vitalidad y empezaron a
interactuar y jugar con otros simios. Conforme presentaban un comportamiento normal, el
medicamento se suspendió gradualmente. Más allá de ser físicamente similares, nuestros
parientes también comparten respuestas emocionales y psicológicas.
A) Son más o menos mil chimpancés los que actualmente son víctimas de la
experimentación en laboratorios gubernamentales de Estados Unidos.
B) Después de vivir encerrados en laboratorios, sometidos a múltiples experimentos,
los chimpancés no pueden tener una vida normal una vez dados de alta.*
C)Debido a la gran similitud genética entre seres humanos y chimpancés, estos
últimos son objeto predilecto de experimentos para la investigación médica.
D)Los chimpancés comparten una importante carga genética con los seres
humanos, y por ello pueden padecer enfermedades como el SIDA.
E) Los chimpancés no solo son físicamente similares al hombre, sino que comparten
con este casi todas sus respuestas emocionales y psicológicas.
SOLUCIÓN: B. La idea principal del texto sostiene que los chimpancés responden
negativamente a los experimentos a los que son sometidos una vez que se los deja en
libertad; por ello se deprimen y no pueden tener una vida normal.
TEXTO 3
Para el ojo poco entrenado, un concierto de heavy metal puede parecer el caos total.
Música violenta a todo volumen, los gritos del vocalista principal y un público que brinca,
empuja y se estrella sin cesar. Sin embargo, para dos jóvenes investigadores, estos
eventos son la clave para entender el comportamiento humano en situaciones extremas.
Sirviéndose de la física, han encontrado un patrón constante dentro del aparente
desorden. Jesse Silverberg y Matt Bierbaum, estudiantes de la Universidad de Cornell y
amantes del metal, han observado durante dos años múltiples conciertos basándose en
teorías de movimiento colectivo y de las propiedades físicas del gas para hacer sentido
del alboroto.
Marcos Elantiguo

Encontraron dos maneras distintivas del baile metalero: quienes se encuentran más
cercanos al escenario saltan, se avientan y chocan entre sí (un comportamiento similar al
de las partículas gaseosas, ya que al viajar en grupos también se aceleran y se golpean);
quienes rodean al grupo central bailan en un círculo rotativo (una conducta parecida al
patrón vórtice de las partículas).
En base a sus observaciones, han creado un modelo computarizado interactivo
capaz de representar el fenómeno. Modelos como este, que permiten recrear numerosas
acciones en cuestión de segundos, podrían ser utilizados en el diseño de espacios más
seguros, ya que podrían predecir las reacciones humanas frente a situaciones de pánico.
En lugares cerrados que contienen grandes masas, reduciría el riesgo de ser pisoteado o
herido.
A) En un concierto de heavy metal, quienes se encuentran cerca del escenario
tienden a saltar, aventarse y a chocar entre sí, como las partículas gaseosas.
B) Ciertos modelos virtuales interactivos permitirían diseñar espacios en los que las
personas se congreguen multitudinariamente de manera bastante segura.
C) Una investigación permite conjeturar que los jóvenes que se mueven al ritmo del
heavy metal muestran patrones de conducta similares a los de ciertas partículas.*
D) Jesse Silverberg y Matt Bierbaum han observado durante dos años la forma en
que los jóvenes se movilizan y socializan en conciertos de heavy metal.
E) Para la gente común, un concierto de heavy metal puede constituir una
manifestación excesivamente caótica y beligerante de música violenta.
SOLUCIÓN: C. La idea que desarrolla esencialmente el tema central sostiene que es
posible determinar patrones conductuales similares a ciertas partículas en conciertos de
heavy metal, gracias a la investigación de Jesse Silverberg y Matt Bierbaum.
TEXTO 4
Se rompen los paradigmas de la neurociencia al demostrarse que es posible sentir
pavor aun cuando no se tiene una amígdala. Durante décadas, se creía que esta pequeña
estructura almendrada en el cerebro era la única responsable de producir miedo. Ahora,
se confirma la existencia de mecanismos alternos capaces de alertarnos frente al peligro.
El investigador Justin Feinstein y su equipo de la Universidad de Iowa, en Estados Unidos,
demostraron que víctimas del síndrome Urbach-Wiethe (enfermedad que ataca a la
amígdala) también pueden sentir miedo en ciertas situaciones.
La amígdala, al detectar altas concentraciones de dióxido de carbono en la sangre,
desencadena ataques de pánico para prevenir la asfixia. Esto ocurre aun cuando se inhala
CO2 en cantidades no letales. Asumiendo que los pacientes con amígdalas dañadas no
sentirían miedo al respirar el gas, los investigadores condujeron un experimento revelador.
Se les pidió a tres personas enfermas de Urbach-Wiethe y a 12 personas sanas que
respiraran a través de una máscara que contenía un 35% de carbón en el aire.
Sorprendentemente, quienes padecían el daño cerebral sintieron incluso más susto y
pánico que los voluntarios sanos: la primera vez, desde su infancia, que experimentaban
el miedo.
Debido a los resultados observados se pudo concluir que, contrariamente a lo que se
pensaba, la amígdala no es esencial en todas las respuestas de miedo. Por lo tanto, el
cerebro cuenta con diferentes sistemas que reaccionan frente a diferentes amenazas,
como es en el caso de ciertos cambios fisiológicos dentro del cuerpo.
Marcos Elantiguo

Este nuevo conocimiento, además de aclarar que existe una distinción entre el miedo
generado por factores externos y el miedo originado por amenazas internas, ha arrojado
luces esclarecedoras en la identificación de estructuras cerebrales desconocidas.
A) Las personas que sufren del síndrome de Urbach-Wiethe experimentan el miedo
en ciertas situaciones a pesar de tener la amígdala dañada.
B) La investigación sobre el miedo desatado a pesar de evidenciar la amígdala
dañada permitió identificar zonas cerebrales ignotas.
C) La amígdala genera reacciones de pavor para prevenir la asfixia cuando los
individuos son sometidos a cantidades ingentes de CO2.
D) Por mucho tiempo se creyó que la amígdala, estructura almendrada localizada en
el cerebro, era la única responsable de producir miedo.
E) Los paradigmas de la neurociencia son transgredidos al demostrarse que se
puede sentir pavor, aun cuando se carece de amígdala.*
SOLUCIÓN: E. La idea principal sostiene que la amígdala no es la causante exclusiva del
miedo; esta afirmación genera una ruptura de los esquemas canónicos en neurociencia.
SEMANA 1 B
ELIMINACIÓN DE ORACIONES
Los ejercicios de eliminación de oraciones establecen dos criterios sobre el manejo
de la información en un texto determinado: a) La cohesión temática y b) la economía de la
expresión. En virtud de estos criterios, la eliminación de oraciones se puede hacer de dos
maneras alternativas: a) O bien, se suprime la oración que no corresponde al tema clave
del conjunto; b) o bien, se suprime la oración redundante, esto es, la que no aporta
información al conjunto.
1. I) El universo maya descansa sobre un gran cocodrilo. II) El dragón bicéfalo cuyo
cuerpo es una banda con símbolos celestes se arquea sobre la diosa de la Luna
para los mayas. III) El universo maya es una confluencia de animales vinculados con
los cuerpos celestes. IV) La luna sostiene la figura del conejo que es el animal
representativo de la superficie lunar para los mayas. V) La cola de una gran
serpiente representa las pléyades del universo maya.
A) V B) I C) IV D) II E) III*
SOLUCIÓN: E. Se elimina el enunciado III por redundancia. El vínculo entre lo animal y el
cosmos está implicado en cada una de las oraciones restantes.
2. I) Los eclipses solares, generados por la confluencia entre el Sol y la Luna, pueden
ocurrir se manera parcial o total. II) El eclipse solar parcial, uno de los cuatro tipos de
eclipse, ocurre cuando la Luna no cubre por completo al Sol, y solo la penumbra toca
a la Tierra. III) El eclipse anular de Sol ocurre cuando la Luna se encuentra más
alejada de la Tierra en su órbita elíptica, lo que genera que la imagen de la Luna sea
menor que la del Sol. IV) Cuando la Luna pasa por la umbra de la Tierra, suceso
visible para la mitad del planeta al mismo tiempo, se genera el denominado eclipse
lunar. V) Es posible que la Luna cubra al Sol completamente, y la corona se torne
visible sobre la superficie solar: tal es el caso de un eclipse total de Sol.
A) I* B) V C) II D) IV E) III
Marcos Elantiguo

SOLUCIÓN: A. Se elimina el enunciado I en virtud del criterio de redundancia. El
contenido informativo de esta oración lo detectamos en II y en V.
3. Los navajos originarios del oeste de América Septentrional suelen denominarse a sí
mismos «el pueblo». II) Los navajos consideran que el cielo centellea con las
constelaciones y la vía láctea, vigilado por un dios del arco iris. III) Cada cuarto
terrestre se caracteriza por un color, una montaña sagrada, la hora del día y una
persona sagrada para los navajos. IV) Unos jóvenes guerreros cargan el sol azul y la
luna blanca en la cosmovisión de los navajos. V) Los navajos creen que una tierra
gobernada por el Gran Viento (amarillo) y el Gran Trueno se encuentra más allá de la
ubicación del sol azul y la luna blanca.
A) I* B) II C) III D) IV E) V
SOLUCIÓN: A. Se elimina el enunciado I en virtud del criterio de inatingencia. El resto de
oraciones aborda la forma en que los navajos entienden el cosmos.
4. I) Hubble se dedicó a medir con paciencia y precisión la distancia hasta las
misteriosas nebulosas espirales que durante mucho tiempo fueron asumidas como
nubes de gas. II) Hubble determinó que las nebulosas espirales difusamente visibles
eran, en realidad, otras galaxias sumamente alejadas que fue descubriendo una tras
otra. III) Hubble, a través de la detección de galaxias desconocidas, transformó la
idea de que todos los cuerpos celestes existentes estaban contenidos en nuestra
galaxia. IV) Hubble descubrió nuevas galaxias midiendo la distancia hasta las mal
llamadas nubes de gas, y dio cuenta de un cosmos en movimiento acelerado. V)
Mediante la medición de la distancia hasta las nuevas galaxias, Hubble se percató de
que el cosmos estaba explotando salvajemente y cada galaxia viajaba a una
velocidad proporcionalmente mayor.
A) V B) III C) I D) IV* E) II
SOLUCIÓN: D. Se elimina el enunciado IV en virtud del criterio de redundancia. La
información de esta oración está incluida en las oraciones I, II y V.
5. I) El «milagro griego», según José Russo Delgado, fue producto de la geografía de
Grecia cuyo porcentaje de costa respecto de su extensión total es muy elevado. II)
Es pertinente indicar que se desarrolló un «milagro» egipcio, hebreo, o caldeo; pero
el que ocurrió en Grecia define los linderos de la filosofía en sí, señala el filósofo
Russo Delgado. III) La adaptabilidad y la claridad de la lengua griega, de evidente
superioridad respecto del egipcio o el hebreo, fue otra de las causas del denominado
«milagro griego» para José Russo. IV) José Russo Delgado sostiene que la
economía griega, carente de trigo como producto comercial, contribuyó a la riqueza
en Grecia y, por ende, a la ocurrencia del «milagro griego». V) Otra de las causas
que determinaron el «milagro griego» es el cariz politeísta de la religión griega,
religión abierta a la influencia de los dioses de los pueblos vecinos.
A) III B) V C) II* D) IV E) I
SOLUCIÓN: C. Se elimina el enunciado II en virtud del criterio de inatingencia. El tema
que cohesiona el contenido oracional es los diversos factores que determinaron el
«milagro griego» según el filósofo José Russo Delgado.
Marcos Elantiguo

6. I) Entre los factores históricos que ocasionan el bilingüismo aparece la expansión de
unos pueblos por territorios donde se habla otra lengua. II) La unificación política
guiada por grupos de poder determina que se impongan ciertos hábitos lingüísticos
y, por consiguiente, que se gesten situaciones de bilingüismo. III) El bilingüismo en el
cual el contacto de dos o más lenguas deviene en la expansión de una de ellas por
su mayor peso demográfico se denomina bilingüismo ambiental. IV) Países y
ciudades que reciben grandes contingentes de inmigrantes determinan que la
migración sea uno de los factores potenciales en la ocurrencia de bilingüismo. V) El
cosmopolitismo presente en lugares de contactos internacionales, por lo general
comerciales y económicos, es uno de los factores que determinan situaciones de
bilingüismo.
A) II B) V C) I D) IV E) III*
SOLUCIÓN: C. Se elimina la oración III en virtud del criterio de inatingencia. Los factores
que ocasionan el bilingüismo constituyen el eje temático; la oración señalada está referida
a un tipo de bilingüismo.
COMPRENSIÓN DE LECTURA
TEXTO 1
Ojos almendrados, orejas delicadas, dedos gráciles y cuello largo y esbelto como el
de un cisne; los labios, carnosos y de trazo elegante; los pómulos, marcados y elevados;
su barbilla era fina y la nariz, estrecha y recta. Es decir, un canon de belleza femenina. ¿O
quizás era corpulenta y cuellicorta, con los hombros caídos, las mejillas fláccidas, los
labios finos y las caderas rollizas?
Tal vez nunca lleguemos a saberlo. Evidentemente, no hay fotos ni dibujos de su
persona; tampoco descripciones de sus contemporáneos. Sigue teniéndosela por una de
las mujeres más poderosas de la Antigüedad —erótica, mayestática, con un indudable
carisma—, pero todo cuanto conocemos de ella proviene de los relieves e inscripciones
tallados en bloques de piedra caliza, y de las interpretaciones que los artistas hicieron de
la soberana en las estatuillas y los bustos que han llegado hasta nosotros, el más famoso
de los cuales fue hallado hace un siglo por arqueólogos alemanes y está expuesto en el
Museo Egipcio de Berlín (Neues Museum). Al entrar en la Sala de la Cúpula Norte y
contemplar su belleza bajo la estudiada iluminación, el observador es presa de su encanto
irresistible. Cada año sucumben a su hechizo un millón de visitantes. Muchos acuden
solamente por verla a ella.
Sabemos que Nefertiti estuvo casada con el faraón Akenatón y que vivió hace casi
tres milenios y medio en un período fascinante de la historia de Egipto. Pero los detalles
de su biografía son caldo de cultivo de especulaciones y un campo de batalla para los
investigadores. «No hay dos opiniones coincidentes sobre esta época», asegura el
eminente egiptólogo y arqueólogo inglés Nicholas Reeves.
1. El tema central del texto es
A) la carencia de fotos y dibujos representativos sobre la vida íntima de Nefertiti.
B) la imagen de Nefertiti representada en inscripciones talladas en piedra caliza.
C) la falta de certeza acerca de la fisonomía y los detalles de la vida de Nefertiti.*
D) el carisma de Nefertiti, una de las mujeres más poderosas de la Antigüedad.
E) la hipótesis taxativa de Nicholas Reeves acerca de la biografía de Nefertiti.
Marcos Elantiguo

SOLUCIÓN: C. El texto desarrolla el tema de la imprecisión que se tiene respecto de la
fisonomía de Nefertiti, que es posible derivar a los detalles de su biografía, la cual motiva
conjeturas cruzadas y opiniones diversas.
2. La palabra PERSONA hace referencia específicamente a la
A) sensibilidad. B) personalidad. C) complexión.*
D) naturaleza. E) idiosincrasia.
SOLUCIÓN: C. En el texto se alude a la incertidumbre que se tiene acerca del físico de
Nefertiti, dado que no existen dibujos ni fotos de su «persona». Por esa razón, la palabra
se relaciona con la constitución física, esto es, la complexión de Nefertiti.
3. La expresión CAMPO DE BATALLA se refiere expresamente a
A) las agresiones de los arqueólogos que investigan la vida de los faraones.
B) la patente avidez mostrada por los visitantes de la reina egipcia Nefertiti.
C) las conjeturas desatadas acerca de la arcana belleza de la reina Nefertiti.
D) las teorías discordantes que se originan respecto de la vida de Nefertiti.*
E) las pugnas ideológicas que los egipcios desatan acerca de sus deidades.
SOLUCIÓN: D. La expresión referida se relaciona con las discusiones o propuestas
teóricas divergentes que los investigadores plantean acerca de la vida o biografía de
Nefertiti.
4. Es posible deducir del texto que el busto expuesto en el Museo Egipcio de Berlín
A) es una representación idealizada que no necesariamente se corresponde con el
aspecto real que tuvo Nefertiti.*
B) fue confeccionado por espiritistas y magos que han hecho que, aun hoy, la gente
se enamore de Nefertiti.
C) constituye un caso paradigmático en el que la representación artística ha seguido
estándares objetivos.
D) permite obtener una versión fidedigna del tremendo carisma que Nefertiti
ostentaba cuando era reina.
E) es la prueba de que los arqueólogos alemanes fueron los únicos en proporcionar
datos sobre la reina Nefertiti.
SOLUCIÓN: A. No existen imágenes concluyentes que corroboren la belleza superlativa
de Nefertiti; algunas representaciones son producto de las interpretaciones que los artistas
han hecho de su figura. De ello se deduce que la imagen visitada solo es una idealización.
5. Resulta incompatible con el desarrollo textual afirmar que los investigadores de
Nefertiti
A) se enfrenta a la indeterminación de los detalles respecto de la vida de esta.
B) se permiten plantear diversas propuestas sobre los aspectos de su biografía.
C) determinaron su matrimonio con Akenatón, y la sitúan en una etapa fascinante.
D) han llegado a un consenso concluyente acerca de los detalles de su biografía.*
E) asumen, como en el caso de Reeves, que las teorías sobre su época divergen.
Marcos Elantiguo

SOLUCIÓN: D. En el texto se desarrolla el tema de la indeterminación que se tiene acerca
de la reina Nefertiti, tanto en lo que concierne a su belleza como en lo relativo a su
biografía; por lo tanto, es incompatible afirmar que existe un consenso de los
investigadores en lo que toca a los detalles de su biografía.
6. Si los bustos y las estatuillas de Nefertiti hubiesen sido creados por artistas signados
por un estilo realista, es probable que
A) el embeleso de los visitantes al Museo de Berlín disminuya notablemente.
B) los debates de los estudiosos sobre la fase de esplendor egipcio crezcan.
C) las opiniones divergentes acerca de la biografía de la reina desaparezcan.
D) bustos, estatuillas e imágenes de los museos sean reemplazados por fotos.
E) la belleza que se le atribuye se corresponda con un referente histórico real.*
SOLUCIÓN: E. Las representaciones son sumamente subjetivas, razón por la que no
existe una prueba fidedigna acerca de la presunta belleza de Nefertiti. Si los artistas
hubiesen tenido una orientación realista, las imágenes de Nefertiti nos mostrarían con
veracidad la complexión real de la reina.
TEXTO 2
En un artículo muy leído dentro de la antropología y la lingüística desde su
publicación original en 1967, Keith Basso describió todo un sistema de denominación de
partes de vehículos de motor en la lengua de los apaches occidentales del centro-este de
Arizona. Los apaches occidentales han extendido el uso de las partes del cuerpo de los
seres humanos y los animales para referirse a las partes de los automóviles y camionetas.
En este sistema estructurado de denominación, el capó se convierte en la nariz (bichih),
los faros son los ojos (bidáá) y el parabrisas se convierte en la frente (bita’). El término
para la cara (bínii’) se extendió a toda la zona que va desde la parte superior del
parabrisas hasta el parachoques delantero, de modo que este término incluía como
subpartes la nariz/capó y la frente/parabrisas. Las ruedas delanteras se convierten en
manos y brazos (bigan), mientras que las ruedas traseras y sus neumáticos son los pies
(bikee’). Todos los elementos debajo del capó se clasificaban como partes de las tripas
(bibiye’). Bajo el capó, la batería se convirtió en el hígado (bizig); los cables eléctricos, en
las venas (bits’ oos); el depósito de gasolina, en el estómago (bibid); el distribuidor es el
corazón (bijíí); el radiador, el pulmón (bijíí’ izólé); los manguitos del radiador, los intestinos
(bich’í). Basso se refirió a la denominación de vehículos en apache occidental como
«extensión de conjunto», sugiriendo que lo sucedido era simplemente que un conjunto de
nombres relativos a los seres animados había extendido su significado para abarcar el
nuevo conjunto de las partes pertenecientes a los vehículos de motor.
Es posible predecir, sobre la base de este sistema descriptivo minucioso de Basso, y
ciñéndonos al conocimiento actual que proporciona la teoría cognitiva gestada por Lakoff y
Johnson en su obra Metaphors We Live By (1980), que los apaches occidentales, cuando
vieron vehículos de motor por primera vez, usaron el cuerpo humano o la fisonomía del
caballo como una metáfora que le permitía hablar de aquellos. La metáfora conceptual
subyacente me permito definirla como LOS VEHÍCULOS DE MOTOR SON COSAS ANIMADAS, y
les posibilitó establecer correspondencias entre las partes de los seres vivos y las partes
de los coches y las camionetas, y denominarlas en consecuencia. En la metáfora LOS
VEHÍCULOS DE MOTOR SON COSAS ANIMADAS, la cosa de la que hablamos (el vehículo de
motor), con sus partes y relaciones constitutivas, es el dominio meta; mientras que la cosa
con la que hablamos (seres animados), con sus propias partes y relaciones constitutivas,
es el dominio origen.
Marcos Elantiguo

1. Fundamentalmente, el tema central gira en torno a
A) la manera exótica en que los apaches en general denominan las partes del cuerpo
mediante secciones de vehículos.
B) la descripción que Basso realiza sobre las metáforas conceptuales que ocurren en
apache para designar las partes de un auto.
C) las metáforas que utilizan los apaches para indicar las partes de los vehículos a
motor, a partir de palabras relativas al cuerpo.*
D) los artículos de investigación que Basso presentó sobre las expresiones apache
referidas al cuerpo de los seres humanos.
E) las palabras apache usadas para referirse al radiador, el capó y las ruedas de las
camionetas y los automóviles modernos.
SOLUCIÓN: C. El tema central del texto es la denominación de las partes de un vehículo
a motor sobre la base del léxico apache referido al cuerpo humano o animal. Se presenta
la descripción de Basso sobre este sistema, y se replantea a través de la teoría cognitiva.
2. En el texto, la palabra CONVERTIR connota
A) intercambio desigual entre cosmovisiones.
B) degeneración de la cosmovisión apache.
C) transformación de las partes de un hombre.
D) modificación del sentido literal primigenio.*
E) desaparición del léxico usado por apaches.
SOLUCIÓN: D. El verbo es usado para indicar la designación de un referente distinto a
través de la palabra apache para hígado; por consiguiente, el sentido literal del término
varía.
3. Se puede colegir del texto que la teoría de la metáfora conceptual planteada en el
texto
A) devino del sistema de clasificación descrito por Basso.
B) asume que el dominio de origen es el único relevante.
C) evidencia el concepto de «extensión de conjunto».
D) sugiere la inflexibilidad significativa de las palabras.
E) fue completamente desconocida para Keith Basso.*
SOLUCIÓN: E. La teoría de la metáfora conceptual fue planteada por Lakoff y Johnson en
el año 1980, mientras que la descripción de Basso es de 1967. La brecha temporal
permite inferir que la propuesta de la metáfora fue desconocida por Keith Basso.
4. Es posible deducir que los apaches occidentales mencionados en el texto
A) desaparecieron al entrar en contacto con la sociedad moderna.
B) mostraron fidelidad hacia las formas léxicas de su lengua nativa.*
C) eran incapaces de respetar sus rasgos culturales al usar autos.
D) vieron en el léxico foráneo para los autos una fuente de cambios.
E) contribuyeron activamente en la constitución de la teoría cognitiva.
Marcos Elantiguo

SOLUCIÓN: B. Los apaches occidentales usaron los elementos léxicos de su lengua
materna; por consiguiente, se deduce que estos mostraron una actitud de fidelidad hacia
sus particularidades lingüísticas.
5. Resulta incompatible con el desarrollo textual afirmar que Lakoff y Johnson sostienen
que la metáfora conceptual
A) se circunscribe a las creaciones de tipo retórico y académico.*
B) involucra la relación entre dominios diferentes (origen y meta).
C) permite que se expresen ciertos dominios a partir de otros.
D) haría posible que la palabra bidáá sirva para decir «faros».
E) permitiría usar correspondencias entre el cuerpo y los autos.
SOLUCIÓN: A. La muestra que nos ofrece el texto es de cariz cotidiano; por tal razón, es
incompatible asumir que la propuesta de la metáfora conceptual se ciñe al ámbito
académico.
6. Si fuésemos incapaces de usar ciertos dominios para referirnos a otros,
posiblemente
A) la teoría de la metáfora conceptual habría sido planteada antes de la descripción
sobre el apache.
B) las expresiones metafóricas podrían explicarse mediante la propuesta semántica
de Keith Basso.
C) se tendrían que crear nuevos y diversos elementos lexicales para expresar las
nuevas realidades.*
D) los préstamos lingüísticos serían insuficientes para cubrir las necesidades
comunicativas.
E) la teoría de la metáfora conceptual solo debería concentrarse en el denominado
dominio origen.
SOLUCIÓN: C. La metáfora conceptual sostiene que somos capaces de relacionar
dominios; esto es, mediante ciertos dominios de origen nos permitimos expresar dominios
meta. Si fuésemos incapaces de realizar esta operación, la creación léxica, entre otros
posibles mecanismos, harían posible la expresión de nuevos referentes.
SEMANA 1 C
SERIES VERBALES
Las palabras no están en nuestra mente como entidades aisladas. Más bien, se
puede sostener con plausibilidad que los vocablos presentan ciertos engarces semánticos
claramente definidos. En el lexicón mental, los vocablos se encuentran reunidos en virtud
de ciertas leyes semánticas de asociación. La noción de serie verbal intenta recoger la
idea de que las palabras no se reúnen por simple yuxtaposición, sino que se organizan en
función de relaciones semánticas definidas.
Ahora bien, las asociaciones léxicas subtendidas por las series verbales son de
variada índole: sinonimia, antonimia, cohiponimia, meronimia, etc. En consecuencia, los
ítems de series verbales son versátiles y plasman la creatividad inherente al lenguaje
humano.
Marcos Elantiguo

1. ¿Cuál de los siguientes términos no forma parte de la serie verbal?
A) Desordenado B) Inatingente C) Estocástico *
D) Inconexo E) Farragoso
SOLUCIÓN: C. La serie verbal está conformada por sinónimos. La palabra «estocástico»
significa ‘azaroso’ y, por ello, queda excluida.
2. Reservado, reticente; cachazudo, veloz; fortuito, casual…
A) felón, inocuo B) proteo, voluble C) basto, palurdo
D) cutre, mezquino E) banal, capital *
SOLUCIÓN: E. La serie verbal es mixta y sigue la siguiente secuencia: sinónimos,
antónimos y sinónimos. Se completa consistentemente con el par de antónimos BANAL
‘trivial, insignificante’ y CAPITAL ‘importante, medular’.
3. Embutir, encajar, llenar…
A) enquistar* B) pergeñar C) flagrar
D) detentar E) gravar
SOLUCIÓN: A. La serie verbal es sinonímica. Se completa con la palabra ENQUISTAR
cuya primera acepción es literalmente «embutir, encajar algo».
4. Fulgir, resplandecer; pauperizar, empobrecer; arrostrar, encarar…
A) zaherir, honrar B) tañer, silenciar C) pungir, herir *
D) paliar, agudizar E) azuzar, reprimir
SOLUCIÓN: C. La serie verbal está formada por pares de sinónimos; por consiguiente, se
completa con el par de palabras que mantiene la relación semántica: PUNGIR y HERIR.
5. Topo, desmán; solípedo, caballo; marmota, castor…
A) panda, osezno B) cebra, onagro C) reno, ñandú
D) cetáceo, narval* E) bufeo, delfín
SOLUCIÓN: D. La serie verbal es mixta y está conformada por pares de palabras cuyas
relaciones semánticas son las siguientes: cohiponimia; hiperonimia-hiponimia, y
cohiponimia. El par de palabras que recoge la relación de hiperonimia-hiponimia es
«cetáceo, narval».
6. Capó, automóvil; ballesta, muelle; espoleta, torpedo…
A) dintel, puerta B) armadura, yelmo* C) pértiga, vara
D) derrame, alféizar E) fuselaje, avión
SOLUCIÓN: B. La serie verbal es mixta, y está conformada por pares de palabras cuyas
relaciones son las siguientes: merónimo-holónimo; holónimo-merónimo y merónimo-
holónimo. Esta se completa con las palabras que recogen la segunda relación; a saber,
«armadura, yelmo».
Marcos Elantiguo

7. Determine la palabra que es antónima de DELETÉREO, PONZOÑOSO y
MORTÍFERO.
A) Dechado B) Munífico C) Inocuo*
D) Venenoso E) Benévolo
SOLUCIÓN: C. La serie verbal está formada por sinónimos. El antónimo de deletéreo,
mortífero, etc., es «inocuo» cuyo sentido literal es ‘inofensivo’.
8. Casual, fortuito, azaroso…
A) aleatorio* B) especulativo C) dubitativo
D) incisivo E) pasible
SOLUCIÓN: A. La serie verbal está formada por sinónimos. La palabra que cierra
consistentemente la relación semántica es «aleatorio».
COMPRENSIÓN DE LECTURA
TEXTO 1
Comúnmente se dice que lo que no se usa se pierde, esto es cierto en el caso de la
mente. Nuevos avances científicos apuntan hacia la Reserva Cognitiva no solo como
preventiva del Alzheimer, sino como esencial en la lucha contra esta. El Alzheimer se
conoce como la enfermedad del siglo XXI. Se trata de la forma más común de demencia y
es incurable, progresiva y terminal. Actualmente, existen alrededor de 36 millones de
afectados a nivel mundial, cifra que aumentará a 115 millones para 2050.
El Dr. Yaakov Stern, Director de Neurociencia Cognitiva del Sergeivsky Center y del
Taub Institute, ha investigado desde la década de los ochenta lo que nombró la Reserva
Cognitiva (RC), o la capacidad de minimizar el deterioro mental. Ha revelado que esta se
adquiere ejercitando el cerebro a través de hábitos mentales saludables. El Dr. Stern pudo
evidenciar la importancia de la Reserva Cognitiva al estudiar el caso de un jugador de
ajedrez quien presentaba leves síntomas de Alzheimer. Tras morir por causas
independientes, reveló en una operación post mortem un estado mucho más avanzado de
la enfermedad del que inicialmente se creía. Su increíble manejo del Alzheimer se debía a
que, gracias a su profesión, su RC era muy alta: nuestro entorno, nuestras capacidades
innatas, la educación que recibimos, el puesto de trabajo que desempeñamos y las
actividades de ocio que elegimos, contribuyen a la elaboración de nuestra Reserva
Cognitiva.
Aunque se encuentra en elaboración, por el momento no existe una escala de
puntuación que mida la Reserva Cognitiva ni se sabe con exactitud qué factores son los
más influyentes sobre ella. Sin embargo, no cabe duda de que el mantenerse activo y
ocupado protege del daño cerebral.
1. ¿Cuál es el tema central del texto?
A) La Reserva Cognitiva y su potencial eficacia en la lucha contra el Alzheimer*
B) La escala de puntuación que hace medible la Reserva Cognitiva en humanos
C) Los factores ignotos que influyen en la constitución de la Reserva Cognitiva
D) La Reserva Cognitiva determinada por el Dr. Stern en un jugador de ajedrez
E) La enfermedad de Alzheimer y su creciente ocurrencia en el presente siglo
SOLUCIÓN: A. En el texto se desarrolla el tema de la Reserva Cognitiva estudiada por el
Dr. Stern y su presunta eficacia en el tratamiento y prevención del mal de Alzheimer.
Marcos Elantiguo

2. Determine la idea principal del texto.
A) La Reserva Cognitiva es una forma eficaz para combatir el deterioro mental
ocasionado por el Alzheimer según Yaakov Stern.*
B) Se desconoce cuáles son, con exactitud, los factores que influyen de manera
notoria en la constitución de la Reserva Cognitiva.
C) El Alzheimer es una forma común de demencia y se caracteriza por ser incurable,
progresiva, terminal y de creciente ocurrencia.
D) El increíble manejo del Alzheimer evidenciado en el jugador de ajedrez
mencionado en el texto se debía al ejercicio mental.
E) La educación que recibimos y el trabajo que desempeñamos son dos de los
factores que contribuyen con la Reserva Cognitiva.
SOLUCIÓN: A. De acuerdo con el tema central, la idea jerárquicamente más importante
sostiene que la Reserva Cognitiva estudiada por Stern es una forma eficaz de combatir el
Alzheimer e incluso de prevenirlo.
3. En el texto, la palabra INDEPENDIENTE supone que la muerte del ajedrecista fue
por
A) el deterioro grave que le causó la demencia.
B) tener índices muy bajos de Reserva Cognitiva.
C) causas ajenas a la enfermedad de Alzheimer.*
D) tener un padecimiento de carácter congénito.
E) la peligrosidad de su profesión y su trabajo.
SOLUCIÓN: C. La muerte del ajedrecista ocurrió al margen del deterioro mental que
ocasiona el Alzheimer; por ello se menciona que fue por causas INDEPENDIENTES.
4. La palabra MANEJO connota
A) dirección. B) maquinación. C) intriga.
D) conducción. E) adaptabilidad.*
SOLUCIÓN: E. La palabra aludida hace referencia al escaso deterioro que causó la
enfermedad de Alzheimer en el ajedrecista, gracias a su alta Reserva Cognitiva. Esto es,
se adaptó de manera positiva a los embates de la enfermedad.
5. Resulta incompatible con la información textual afirmar que las actividades de ocio
escogidas por las personas
A) podrían constituir una buena forma de entrenamiento de la mente.
B) carecen de relevancia en la constitución de la Reserva Cognitiva.*
C) hacen posible, cuando involucran ejercicios mentales, una buena RC.
D) constituyen uno de los factores que permiten la elaboración de la RC.
E) podrían permitirles a estas ejercitar de forma apropiada el cerebro.
SOLUCIÓN: B. En el texto se afirma de manera clara que las actividades de ocio, entre
otras causales, definen nuestros índices de Reserva Cognitiva. Por ello afirmar que
carecen de relevancia es incompatible.
Marcos Elantiguo

6. Es incongruente con lo señalado en el texto sostener que la Reserva Cognitiva
A) se mide con precisión solo si se cuenta con una historia clínica adecuada.*
B) minimiza el grave deterioro mental ocasionado por el mal de Alzheimer.
C) es posible que se constituya si se entrena el cerebro de manera sostenida.
D) de un ajedrecista, dado el ejercicio mental, alcanzaría niveles muy altos.
E) carece de pruebas concluyentes respecto de los factores que la generan.
SOLUCIÓN: A. En el último párrafo se indica que no existe una escala de medición de la
RC; por consiguiente, afirmar que es medible resulta una negación de tal idea.
7. Respecto de la enfermedad de Alzheimer, se puede colegir que
A) se trata de un tipo de demencia ignoto y sumamente agresivo.
B) no existe un método eficaz que permita detener su crecimiento.*
C) es combatido por los ajedrecistas mediante técnicas de juego.
D) solo se cura si las actividades de ocio incluyen mnemotecnias.
E) apareció en los manuales de medicina a inicios del siglo XXI.
SOLUCIÓN: B. La cifra de personas que padecerán de Alzheimer crecerá a 115 millones;
por lo tanto, no existe un método que detenga el acelerado crecimiento de esta
enfermedad.
8. Si el ajedrecista mencionado en el texto hubiese evidenciado un deterioro
sumamente grave de sus capacidades cognitivas antes de morir, es posible que
A) el siglo XXI sea el periodo en el que la enfermedad de Alzheimer sea combatida
de manera eficaz y su crecimiento acelerado se detenga.
B) los orígenes de la Reserva Cognitiva sean determinados de manera taxativa junto
con una escala de medición del Alzheimer bastante precisa.
C) el Dr. Yaakov Stern recomiende que los ejercicios mentales, saludables para la
mente, se practiquen a temprana edad y consistentemente.
D) la propuesta de la Reserva Cognitiva motivada por el ejercicio mental para frenar
el deterioro ocasionado por el Alzheimer sea implausible.*
E) los trabajos que demanden el menor esfuerzo físico sean recomendables para
contrarrestar los efectos de la enfermedad de Alzheimer.
SOLUCIÓN: D. La actividad del ajedrecista permite la conjetura de que el ejercicio mental
impide un deterioro agresivo. Si aquel hubiese dado muestras de una pérdida evidente de
sus capacidades cognitivas, asumir que la RC, motivada por el ejercicio mental, resultaría
insostenible.
TEXTO 2
Sócrates (470-399) no dejó nada escrito, de modo que casi todo lo que sabemos de
él procede de los diálogos filosóficos de su discípulo Platón. Estos diálogos, en los que
casi lo escuchamos hablar, nos lo muestran como una figura tan viva que ha quedado
grabada en la memoria de quienes los han leído.
Sócrates era hijo de un escultor y de una comadrona. Empezó dedicándose a la
escultura y después se hizo sofista, pero pronto atentó contra las reglas de este gremio: a
él no le interesaba enseñar trucos verbales sino la fundamentación moral de la política.
Como vio que la religión ya no podía cumplir esta tarea, intentó educar a la élite de Atenas
en el pensamiento independiente, para hacerla así capaz de gobernar. Muy
Marcos Elantiguo

probablemente, detrás de este intento estaban sus malas experiencias con esa
democracia amateur que era el poder del vulgo (oclocracia). Ciertamente, Sócrates
pertenecía a la clase media y vivía modestamente, pero eligió como discípulos a personas
de origen aristocrático, pues su objetivo era formar élites democráticas a través de la
educación. Como enseñaba por vocación, no cobraba nada. Pero su esposa Xantipa no
entendía de ningún modo que la búsqueda de la esencia de la virtud fuera más importante
que la comida en la mesa, y tuvo con él intensas discusiones, que seguramente Sócrates
aprovechó para seguir perfeccionando su dialéctica. Es probable que tuviera un lazo
afectivo muy fuerte con su madre, pues a su propia técnica la denominó «arte de la
comadrona» (mayéutica).
Así pues, Sócrates hizo que la filosofía dejase de ocuparse de la naturaleza para
pasar a ocuparse de la sociedad. Puso los trucos de los sofistas al servicio de la
búsqueda de la verdad y desarrolló el denominado método socrático: Sócrates empezaba
presentándose como alguien que no sabía nada y preguntaba a su interlocutor,
aparentemente seguro de sí mismo, cosas obvias —«¿No es, Critias, el escultor anterior a
la estatua?» Y Critias respondía: «Obviamente»—, después hacía que su interlocutor se
enredara en contradicciones, que resbalara, para acabar mostrándole, cuando este ya
estaba totalmente desorientado y desmoralizado, que la presunta seguridad de sus
opiniones no era más que una forma mitigada de su ignorancia. Este principio de
autodestrucción dirigida se conoce con el nombre de ironía socrática. Se trata de un
método muy espectacular que deja profundas huellas en quien lo sufre. Pero también
muestra claramente en qué consiste la filosofía socrática: en convertir en un problema lo
que parece obvio y en romper el automatismo de las propias percepciones; y, de esta
manera, desmontar el mundo para volver a construirlo bajo el control de la lógica.
1. El tema central que el autor expone es
A) el sustento moral de la política para Sócrates y los sofistas.
B) la paradigmática vida de Sócrates en los diálogos platónicos.
C) el carácter de la filosofía socrática y su método mayéutico.*
D) la autodestrucción moral de Critias, inducida por Sócrates.
E) la democracia aristocrática, propuesta política de Sócrates.
SOLUCIÓN: C. En el texto se sostiene que la filosofía de Sócrates dejó de ocuparse de la
naturaleza para orientarse hacia la sociedad, concretamente a la fundamentación moral
de la actividad política. Igualmente, expone con cierta amplitud, el método mayéutico de
Sócrates.
2. En el texto, el término DESMONTAR connota
A) el descubrimiento de falacias subyacentes.*
B) la puesta en evidencia de la soberbia humana.
C) desmoralización y destrucción del interlocutor.
D) la manifestación de aquello que parece obvio.
E) la eliminación de las percepciones directas.
SOLUCIÓN: A. Según el contexto, esta palabra connota descubrir las falacias que
subyacen en las percepciones. Se deduce que el mundo se asienta sobre estas falacias,
las cuales deben ser descubiertas o desmontadas para construir la verdad bajo el
control de la lógica.
Marcos Elantiguo

3. Del texto se deduce que la ironía socrática aplicada al ateniense Critias
A) obligó a este a reflexionar profundamente en torno a las preguntas de su
interlocutor.
B) pretendía que este fuera objeto de burla por quienes eran testigos de la
indagación.
C) habría sido estéril si este hubiera carecido de opiniones aparentemente
seguras.*
D) tenía como finalidad que este sofista se sintiera completamente seguro de sus
argumentos.
E) fue una advertencia para que otros como este renunciaran a sus opiniones
seguras.
SOLUCIÓN: C. La ironía socrática se aplica a interlocutores que aparentemente cuentan
con opiniones seguras.
4. Es incompatible con las ideas políticas de Sócrates afirmar que este
A) era partidario de la formación de una élite de dirigentes provenientes de la
aristocracia.
B) pese a su procedencia social, desconfiaba de la clase media tanto como del
pueblo.
C) era muy tolerante con la oclocracia por ser una forma de democracia en poder del
vulgo.*
D) estaba completamente convencido de que la educación debía estar al servicio de
la política.
E) consideraba que la política fundada en la moral era garantía de un gobierno
virtuoso.
SOLUCIÓN: C. Este enunciado es incompatible porque Sócrates tuvo malas experiencias
con esa democracia amateur que era el poder del vulgo; por ello, no podía ser tolerante
con este tipo de gobierno.
5. Si Xantipa, esposa de Sócrates, hubiera asumido como suyas las ideas de su
esposo en torno al cultivo de la virtud,
A) Sócrates habría padecido una tensión mayor en su vida familiar y en su actividad
filosófica.
B) la ironía socrática habría evidenciado un carácter menos confrontacional y crítico
con el adversario.
C) la armonía y la felicidad entre los esposos habría sido duradera y ejemplar en la
sociedad ateniense.
D) la práctica de la ironía socrática con su esposa habría sido nula en el contexto de
su vida familiar.*
E) Xantipa habría alcanzado la misma perfección que Sócrates en el manejo del
método mayéutico.
SOLUCIÓN: D. En este contexto, Sócrates no habría podido aplicar su método basado en
la ironía.
Marcos Elantiguo

6. Si las percepciones dieran lugar a profundas indagaciones en torno a su naturaleza y
a su sentido,
A) Sócrates habría abandonado la ironía como método de indagación y crítica.
B) las opiniones seguras se asumirían con mayor confianza en su veracidad.
C) la mayéutica socrática carecería de importancia en la búsqueda de la verdad.
D) se superaría el automatismo con el que se admiten dichas percepciones.*
E) la verdad se alcanzaría de manera armoniosa, sin recurrir a la discusión.
SOLUCIÓN: D. En este caso se superaría el automatismo con el que se admiten las
percepciones, pues estas, antes de ser aceptadas como verdad, estarían sujetas a
profundas indagaciones.
Aritmética
EJERCICIOS DE CLASE N° 1
1. En la siguiente tabla, halle la conclusión de la proposición compuesta.
A) VVVV B) VFFF C) FFFF D) VVVF E) VFFV
(Solución)
Clave E
2. Determine cuál o cuáles de las siguientes proposiciones son contradicciones.
I)  (p ~ q) q p  
II)  (~ p q) (r ~ r) q   
III) p ~q ~p q( ) ( )  
IV)     qpp ~~qp~~ 
A) III y IV B) I y III C) Solo III D) Solo IV E) II y IV
(Solución)
I)  (p ~ q) q p     Vpp  q
II)  (~ p q) (r ~ r) q       qqVqV  qp~
III) p ~q ~p q( ) ( )       Fpp  q~~q~
IV)          Fqpqpqpp  ~~~qp~~
Clave A
p q (~ p  q)  (p  ~ q)
V V
V F
F V
F F
p q (~ p  q)  (p  ~ q)
V V F V V V V V F
V F F F F F V V V
F V V V V F F F F
F F V V F V F V V
Marcos Elantiguo

3. ¿Cuál o cuáles de las siguientes proposiciones son siempre verdaderas?
I)    pq~qp 
II)   qqqp  )(
III)   qqqp  )(
A) Solo I B) Solo II C) Solo III D) I, II y III E) I y II
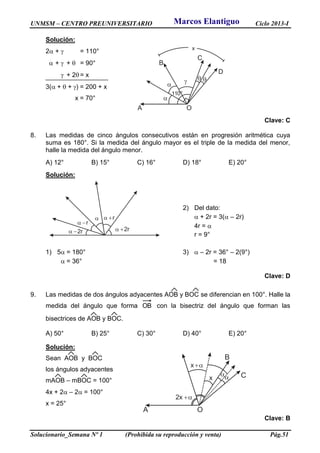
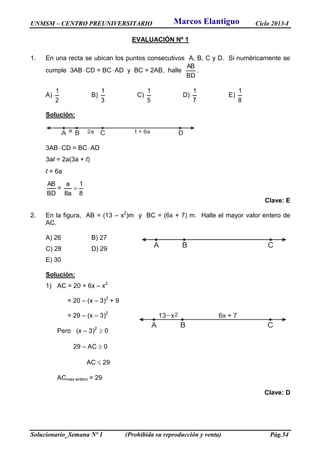
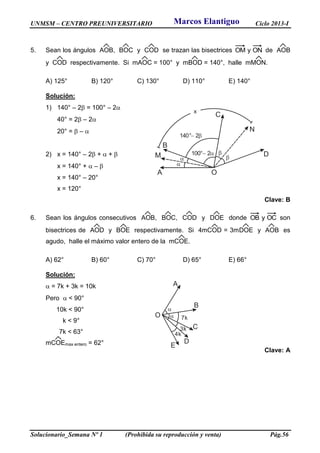
(Solución)
I)    ~p q q p p V p p p V          
II)  ( )p q q q q q V     
III)       Vqqpqqpqqqp  )(
Clave D
4. Si (p  q) v (r  s) es falsa, halle el valor de verdad de las siguientes
proposiciones en el orden indicado.
I) p Δ (q  r)
II) p  (s v r)
III) [ (p  q) v r ]  t
A) VVV B) VVF C) VFV D) FVF E) FFF
(Solución)
    FrVsqpFsrqp
F
FV
F
FV


















 ,

I) p Δ (q  r)   VFVFVV 
II) p  (s v r)   FVFVFF 
III) [ (p  q) v r ]  t    VtFtFFV 
Clave C
5. Si la proposición [ (p  ~ q)  (r  s) ]  [~ s  r ] es falsa, hallar el valor de
verdad de las proposiciones p, q, r y s, en este orden.
A) VVFF B) VVVF C) VFFF D) VFVF E) FVFV
(Solución)
      FrsqVpFrssrqp
F
FV
V
V
FF
V
VV














































 ,,

  

Clave C
Marcos Elantiguo

6. De las siguientes proposiciones:
I) ~ p  ~ q II) ~ (p  q)  p
III) ~ p  (~ p  ~ q) IV) ~ p  ~ (p  q)
¿cuántas son equivalentes a la proposición (p  q)  ~ p ?
A) 0 B) 1 C) 2 D) 3 E) 4
(Solución)
    qppqppqp 
I) ~ p  ~ q Si
II) ~ (p  q)  p   ppqp  No
III) ~ p  (~ p  ~ q) p No
IV) ~ p  ~ (p  q) qp  Si
Clave C
I) p  (p  q) II) (p  q)  q III) (p  q)  (p  t)
¿cuál o cuáles son implicaciones lógicas?
A) Solo I B) Solo II C) Solo III D) I y III E) II y III
(Solución)
I) p  (p  q)   qpqpp  No
II) (p  q)  q    qpqqp  No
III) (p  q)  (p  t)         Vtqpptpqp  Si
Clave C
8. Al simplificar la proposición
         ~ ~q ~p ~ ~p ~q p ~ q p q ~r p q r                    ( )
se obtiene
A) qp  B) qp  C) )( qp 
D) )( qp  E) qp 
(Solución)
              
           
       
       
 
 qp
Fqp
rqprqqp
rqprqqp
rqprqpqpqp
rqprqpqpqppq






Clave C
Marcos Elantiguo

9. Se define los conectivos lógicos  y mediante:
p  q ≡ ~ p  ~q ; p q ≡ ~ p  q
Al simplificar (~p ~ q)  (~q p) se obtiene
A) p  ~ q B) q C) p  q D) p E) p  ~ p
(Solución)
(~p ~ q)  (~q p)    pqqp 
   pqqp 
  pqqp 
qp 
Clave A
10. Si qp  ≡ qp , simplifique la proposición     qqpqp  .
A) q B)  q C) qp  D)  p E) p ↔ ~p
(Solución)
         
    
    qpqpqp
qqpqp
qqpqp


 qqpqp
Clave C
11. Sea la tabla de verdad de la proposición p # q
p q p # q
V
V
F
F
V
F
V
F
V
V
F
V
Si    s#r#q#p es falsa, ¿cuál o cuáles de las siguientes proposiciones son
verdaderas?
I) rp  II) rs  III) qp 
A) Solo I B) Solo II C) Solo III
D) Solo I y II E) I, II, III
(Solución)
qpqqp  ppq# # # #
F V V V
F
F
p q r s F
 
  
      
  
I) rp  F V V  
II) rs  V V V  
III) qp  V V V  
Marcos Elantiguo

12. Al simplificar la proposición
               pqqprqΔpprqprq  ~~~
se obtiene
A) rp B) qp  C) rq  D) qq  E) pp
(Solución)
           q r p q r p p q r p q q p                         
            p q r p q r p q r p q q p                         
            p q r p q r p q r p q q p                         
            p q r p q r p q r p q q p                         
            p q r p q r p q r p q q p                         
       F p q r p q q p            
 F
Clave E
EJERCICIOS DE EVALUACIÓN N° 1
1. Si (p  ~ t)  (s  w) es verdadera y ~ w  ~ s es falsa, hallar el valor de
verdad de las proposiciones p, t, s y w , en este orden.
A) FVVF B) FVFF C) FFFF D) VVVF E) VVVV
(Solución)
 
V F F V F
F
F
w s s w F p t s w V
 
 
        
  
 
Clave A
I) [ (p  r) (p  q)]  [p  (r  q)] II)  ( p  q )  (q  p )
III) p[p  (p  q )] IV) [ ( p  q )]   (qp)
¿cuántas son tautologías?
A) 0 B) 1 C) 2 D) 3 E) 4
(Solución)
I) [ (p  r) (p  q)]  [p  (r  q)]      p r p q p r q            
       p r p q p r p q V               Si
Marcos Elantiguo

II)  ( p  q )  (q  p )    p q q p    No
III) p[p  (p  q )]  p p p q V       Si
IV) [ ( p  q )]   (qp)    p q p q    No
Clave C
3. Sea la tabla de verdad de la proposición p  q
halle la proposición equivalente a (p  q)  p.
A) p  q B) p  q C) p  q D) ~ p E) ~ q
(Solución)
p q q p q p p q      
     * *p q p p q p p q p p q p q         
Clave A
4. Al simplificar la proposición [ p  ( p  q ) ]  [ p  ( q  p ) ], se obtiene
A) p B) q C) p D) p v p E) q  q
(Solución)
         
   
p p q p q p p p p q q p
F p q q p F
                    
       
Clave E
5. Si la proposición {(q→p)  (q→~t)}  (~qΔ~s) es falsa, determine el valor de
verdad de las siguientes proposiciones, en el orden indicado.
i) (p Δ ~s)  (p  r) ii) (r t)  (s  q) iii) (t Δ p)  (p  q)
A) VVF B) FVV C) FFV D) FVF E) FFF
(Solución)
V F V V F V
F F
FF
q p q t q s F
    
     
                          
p q pq
V V V
V F V
F V F
F F V
Marcos Elantiguo

i) (p Δ ~s) → (p  r)      F F p r F p r V       
ii) (r →t)  (s ↔ q)    r V V V V V V      
iii) (t Δ p)  (p ↔ q)    V F F V V F F      
Clave A
6. Si las siguientes proposiciones      pqytpqp  son tautologías,
determine el valor de verdad de p, q y t, en el orden indicado.
A) VFV B) VFF C) VVF D) FVV E) FFF
(Solución)
VV V V F V
FF F
F
p q p t q pV V     
   
     
              
  
Clave C
7. Al simplificar  {(p  q)  [(p  q)  (p  q)]}  {(q  p)  [p  (q  p)]} ,
se obtiene
A) q  q B) p  q C) p  q D) p  p E) p  q
(Solución)
 {(p  q)  [(p  q)  (p  q)]}  {(q  p)  [p  (q  p)]}
≡ {(p  q)  [ (p  q)  (p  q)]}  {(q  p)  (p  q)}
≡ {(p  q)  [ (p  q)  (p  q)]}  {(p  q)  (p  q)}
≡ (p  q)  {(p  q)  (p  q)}
≡ (p  q)  (p  q)
≡ p  q
Clave C
I) t  (p  q) II) ~ t  (p  q) III) ~ q  (~ t  p)
¿cuál o cuáles son equivalentes a la proposición ~ p  (q  ~ t)?
A) Solo I B) Solo II C) Solo III D) I y III E) II y III
(Solución)
   p q t p q t    
I) t  (p  q)  t p q   Si
II) ~ t  (p  q) No
III) ~ q  (~ t  p)  q t p   Si
Clave D
Marcos Elantiguo

9. Si pqqp  , entonces el equivalente de la proposición
      ppppqp  es
A) p~p B)  p  q C)  q
D) p~p E) p
(Solución)
      
      
 
p q p p p p
p q p p p p
p q V V
       
     
   
Clave A
10. Simplifique                 rqppr~q~pqppq~qp~ 
A) p B) q C) p~p D) p~p E) qp 
(Solución)
             p q q p p q p q r p p q r                     
              p q q p p q p q p r p q r                     
              p q q p p q p q p r p q r                     
            p q q p p q p q r p q r                    
       p q q p p q V       
 V
Clave D
Álgebra
EJERCICIOS DE CLASE
1. Hallar la diferencia positiva de los valores de n que hacen que la expresión
algebraica  
   
 
5
2nn
4n5n
60
2n
18
zyxz,y,xH


 sea racional entera.
A) 7 B) 9 C) 3 D) 5 E) 11
Solución:
Se debe cumplir:
  
  






ZZZ
5
2nn
,
4n5n
60
,
2n
18
Marcos Elantiguo

  
  
 
538:ndevaloreslosdepositivaDiferencia
3n,8n
5
2nn
,
4n5n
60
,
2n
18
Si
3n,8n
4n5n
60
y
2n
18
Si
3n,5n,8n,11n,20n
2n
18
Si
















ZZZ
ZZ
Z
Clave: D
2. Simplifique .
3
3.63
M
yx yx
yx
y2
yx
x2
 



A) 3 B) 4 C) 5 D) 6 E) 7
Solución:
5M
5233.63M
3.63
3
3.63
M
1
yx
xy
yx
yx
yx
yx
yx
y2
yx
x2













Clave: C
3. Al simplificar
2
1
3
3313
3
3
1
3
x



















 



 
, halle el exponente de x.
A)
3
1
B) –
3
1
C) 3 D) – 3 E) 3 3
Marcos Elantiguo

Solución:
3
1
:xdeExponente
xxxx
1
333333
33
33
3
333
3
3














Clave: A
4.
x
3
1
x6
x
1
x
1
Ndevalorelhalle,
3
1
xSi









 .
A) 9 3 B) 3 9 C) 3 3 D) 1 E) 9 9
Solución:
9
99
2
19
2
9
2
x
1
x9
2
13
1
x6
x.x6x.x6
9N
93
3
1
N
xx
x
1
N
x
1
x
1
Nluego
3
1
3
x
1
1
x
3
1

















































































Clave: E
5. Si








































m
m
1
m
1
m
m
1
m
m
1
mVdevalorelhalle,3
m
1
m .
A) 16 B) 20 C) 12 D) 24 E) 28
Marcos Elantiguo

Solución:
20V
20182Vluego
18
m
1
m27
m
1
m
m
1
m3
m
1
m
27
m
1
m3
m
1
mcomo
m
1
m2
m
1
2mV
3
m
1
mcomo
m
1
11mV
m
1
m
m
1
mV
3
3
3
3
3
3
3
3
3
3
m
m
1
m
m
1
m
1
m
m
1
m

















































































































Clave: B
6. Simplifique .555125T
2
2
23
2
36
2
13














 















A) 4 5 B) 5 2 C) 5 5 D) 5 25 E) 5
Solución:
347
2
3623243 5555T















Marcos Elantiguo

5T
55T
5555T
347
2
347
2
3
347
2
3823
2
347
2
341













































Clave: E
7. Si
  0x;
x...xxx...xxx
x...xxx
x
vecesx
nnn
vecesn
n3n3n3x
vecesx
nn5
x
2n2
xx
2n
2...x





 

 


  
  
  
, halle el
valor de x.
A)
2n 2n B) n n C)
2n n D) n 2n E) 2n
Solución:
2
2
...2
...
x
2
2
2
22...
x
n 2
2n2xnx
1nn5
1nn6
n2n
n
n3
nnn5
x
nx
nxnxxx
x
x
x.xx.x
x.xx
x


























Clave: A
8. Simplifique
n381
n3
1n3
3
3 38M










.
A) 1 B) 4 C) 2 D) 8 E) 16
Marcos Elantiguo

Solución:
2M
22M
28M
n3 n3
n3 n3.4
n3
n31n3n3
n3
1n3
81 8181 3
81 381
3
33























Clave: C
EJERCICIOS DE EVALUACIÓN
1. Hallar la suma de los valores enteros de n para que la expresión algebraica
  24n 123
5
n10 24
1
3n 9n
yxx
y
y
x
x
y,xH



 











 sea racional entera.
A) 15 B) 14 C) 12 D) 13 E) 16
Solución:
I. Se debe cumplir    14n,n10,3n  Z
 
 
   
1376:nsuma
noyyxy,xH8nSi
xyyxy,xH7nSi
yxyxy,xH6nSi
:emplazandoRe:II
8n,7n,6n6n,n8,5n
24n,2n10,23n
27
233
334
5
12






Clave: D
2. Simplifique .xM
1
1x
x
x
x















A) x B)
3
x C) x D) 2x E) 2x
Marcos Elantiguo

Solución:
xM
xxxM
1
xx
1
x
1
x x.x
x
x



























Clave: C
3. Simplifique
 
1
3
1
27
2
64
1
N
























A) 1 B) 2 C)
2
1
D) 4 E)
4
1
Solución:
 
2
1
N
2
1
2222N 13
1
33
27
2
1
6
3 27
13
1
























 






Clave: C
4. Si 0x;64x
4x  , halle el valor de .
x2
6x2x
V
4
48 

A) 28 B) 32 C) 40 D) 37 E) 42
Solución:
 
37V
82
6828
x2
6x2x
Vluego
8xy8x8x
8x8xComo
44
2
4
4
2
4
448
x
4
4
2x2x
4
44

























Clave: D
Marcos Elantiguo

5. Si
3
...x2x2
Ly...xx3666...66
radicales2012


  
, halle el
máximo valor de R y;18y12y2L44LT 22 .
A) 2 B) 8 C) 6 D) 10 E) 4
Solución:
 
 
 
 
4TMáximo3ysi
y,3y2-4T
y,9y6y22LT
Luego.II
4L1262x2L3
L3x2L9...x2x2x2L9
...x2x2L3
3
...x2x2
L
6xx636
...xxx6...xx6
...xx3666...66
ndoSimplifica.I
2
22
22
2
radicales2012






 








R
R
  
Clave: E
6.  ZnSi satisface la igualdad n26nn248nn224n xxxxxx
222
  ,
entonces
   
     
a
aaa
aaa
1n4n34n6
1nn1n
P 


 es múltiplo de:
A) n + 3 B) 2n + 1 C) 3n – 2 D) n + 7 E) 3n + 2
Marcos Elantiguo

Solución:
  
a
aaa
aaa
a
aaa
aaa
2
2n28n
24n2248n
n2n22n248n6n4n
n26nn248nn224n
15
1
12
1
20
1
543
151220
543
P
emplazandoRe:II
4n02n4n08n2n
n28nxx
1xxx1xxx
xxxxxx
xxxxxx
2
2
222
222












 



 







4npues2n3demultiploes60P
60P
6060
60
453
543
P
a a
a
a
aaa
aaa






Clave: C
7. Si
4 5 82
4
3 5
2244
ba
abbaba
M





 , halle el valor de 6M .
A)  13
ab B)  7
ab C)  5
ab D)  11
ab E)  9
ab
Solución:
   
 
   
   
 136
6
13
30
65
5
1
30
71
5
30 71
40 8
3 524
abM
ababM
ab
ab
ab
ab
ababab
M




Clave: A
Marcos Elantiguo

8. Si
a
n
a a aa
1a a  







  
, halle el valor de n.
A) a aa B) a1a aa  C) aa aa D) a1a aa  E) a a
Solución:
a1a
a
1
1aaa1
aa
aaa
a
a
n
a
a
a
n
a a
aan
aaa
a
a
n
anaaa
aaaa
1
1
1
n
1aa
1a
a
1a a




















































 
Clave: B
Geometría
EJERCICIOS DE LA SEMANA Nº 1
1. En una recta se ubican los puntos consecutivos A, B, C y D. M y N son puntos
medios de AB y CD respectivamente. Si AC = 15 m y BD = 25 m, halle MN.
A) 15 m B) 19 m C) 22 m D) 25 m E) 20 m
Solución:
A B C DM
a a l
N
b b
15
x
25
AC = 15 m  2a + l = 15
BD = 25 m  2b + l = 25
2a + 2b + 2l = 40  a + b + l = 20
x = 20
Clave: E
Marcos Elantiguo

2. En una recta se ubican los puntos consecutivos A, B, C, D y E tales que
AB + BE + BD = 38 m y AB + DE = 11 m. Halle AE.
A) 12,5 m B) 10 m C) 15,5 m D) 24,5 m E) 28,5 m
Solución:
A B C ED
AB + BE + BD = 38 m
AE + BD = 38 m
AE – BD = 11 m
2AE = 49
AE = 24,5 m
Clave: D
3. En una recta se ubican los puntos consecutivos A, B, C y D tales que BC = 4 cm y
mAD – BC – nAC = mBD. Si m = 2n + 1, halle AB.
Solución:
A B C D
4
mAD – BC – nAC = mBD
mAD – mBD = BC + nAC
m(AD – BD) = 4 + n(AB + 4)
mAB = 4 + nAB + 4n
mAB = 4(1 + n) + nAB
AB =
nm
)n1(4


AB =
1n
)n1(4


 AB = 4 m
Clave: D
4. En una recta se ubican los puntos consecutivos A, B, C y D tales que
2AB  CD = 3BC  AD y numéricamente 1
AC
5
BC
2
 . Halle CD en centímetros.
Marcos Elantiguo

Solución:
A B C D
b
a x
Del dato:
CD
BC
2
3
AD
AB

x
a
2
3
bx
ab



2xb – 2ax = 3ax + 3ab
2xb – 5ax = 3ab
x(2b – 5a) = 3ab
Clave: C
5. En la figura, numéricamente se cumple 9(CD – BC) = BC  CD y 1
AC
CD
AB
AC
 .
Halle AC en metros.
A) 5 m B) 7 m C) 9 m D) 11 m E) 13 m
Solución:
9(CD – BC) = BCCD
9
1
CD
1
BC
1
9
1
CDBC
BC
CDBC
CD




. . . (*)
Del dato:
A B C D
x
3
AC
5
BC
2
x
3
b
5
a
2
x
3
ab
a5
ab
b2



Luego:
1
x
3

x = 3
Marcos Elantiguo

*)De(
9
1
AC
1
CD
1
BC
1
AC
1
CDBC
BC
CDBC
CD
AC
1
)BCCD(ACCDBC
)ACCD)(BCAC(AC
)ACCD(ABAC
ACABCDABAC
1
AC
CD
AB
AC
2
2
2











AC = 9 m
Clave: C
6. La tercera parte de la mitad del complemento del suplemento de la medida de un
ángulo excede en 8° a los
5
3
del complemento de la mitad de la medida del mismo
ángulo. Halle el suplemento de la medida de dicho ángulo.
A) 10° B) 12° C) 14° D) 15° E) 18°
Solución:











 
15
165
10
3
548)90(
6
1
5
3
8
2
1
3
1
165
2
S
CCS
Clave: D
7. Sean los ángulos consecutivos AOB, BOC y COD. Si mAOC = 110° y las
bisectrices de los ángulos AOB y COD son perpendiculares, halle mBOD.
A) 50° B) 60° C) 70° D) 80° E) 65°
Marcos Elantiguo

Solución:
2 +  = 110°
 +  +  = 90°
 + 2 = x
3( +  + ) = 200 + x
x = 70°
Clave: C
8. Las medidas de cinco ángulos consecutivos están en progresión aritmética cuya
suma es 180°. Si la medida del ángulo mayor es el triple de la medida del menor,
halle la medida del ángulo menor.
A) 12° B) 15° C) 16° D) 18° E) 20°
Solución:
2) Del dato:
 + 2r = 3( – 2r)
4r = 
r = 9°
1) 5 = 180° 3)  – 2r = 36° – 2(9°)
 = 36° = 18
Clave: D
9. Las medidas de dos ángulos adyacentes AOB y BOC se diferencian en 100°. Halle la
medida del ángulo que forma OB con la bisectriz del ángulo que forman las
bisectrices de AOB y BOC.
A) 50° B) 25° C) 30° D) 40° E) 20°
Solución:
Sean AOB y BOC
los ángulos adyacentes
mAOB – mBOC = 100°
4x + 2 – 2 = 100°
x = 25°
Clave: B

A
B
C
D
 
110°


O
x
 2r

 r
 r
 2r

x

2x 
x
A
B
C
O
Marcos Elantiguo

10. En la figura, halle el máximo valor entero de y cuando x toma su mínimo valor entero.
A) 46°
B) 30°
C) 41°
D) 44°
E) 45°
Solución:
1) x + y + x – y > 90°
x > 45°
xmin entero = 46° . . . (1)
2) Como x – y > 0
x > y
De (1): 46° > y
 ymax entero = 45°
Clave: E
11. En una recta se ubican los puntos consecutivos A, B, C, D, E y F. Si AB = EF =
3
BE
y AC + BD + CE + DF = 24 m, halle BE.
A) 6 m B) 9 m C) 12 m D) 16 m E) 18 m
Solución:
A B C D E F
3a
a a
AC + BD + CE + DF = 24
AB + BC + BC + CD + CD + DE + DE + EF = 24
AF + BE = 24  5a + 3a = 24
a = 3
BE = 3a = 3(3) = 9 m
Clave: B
12. En una recta se ubican los puntos A, B, C, D y E tales que AB + CE = 28 m,
BE – CD = 22 m y AE – DE = 20 m. Halle AE.
A) 30 m B) 33 m C) 35 m D) 36 m E) 40 m
A
M
B
C
x+y
x y
O
Marcos Elantiguo

Solución:
A B C D E
a b c d
AB + CE = 28  a + c + d = 28
BE – CD = 22  b + c + d – c = 22
AE – DE = 20  a + b + c + d – d = 20
2(a + b + c + d) = 70
a + b + c + d = 35
AE = 35
Clave: C
13. Sean los ángulos adyacentes AOB y BOC. Si mAOC + mBOC = 160° y OD
bisectriz de AOB, halle mCOD.
A) 60° B) 40° C) 80° D) 100° E) 90°
Solución:
mAOC + mBOC = 160°
2 +  +  = 160°
 +  = 80°
x = 80°
Clave: C
14. Sean los ángulos consecutivos AOB y BOC tales que mAOB – mBOC = 34°. Se
traza OM bisectriz del AOC. Halle mMOB.
A) 17° B) 34° C) 68° D) 12° E) 22°
Solución:
mAOB – mBOC = 34°
2 +  –  = 34°
 = 17°
mMOB = 17°
Clave: A
A
D
B
C
O
 
x

A
M B
C
O

 
Marcos Elantiguo

EVALUACIÓN Nº 1
1. En una recta se ubican los puntos consecutivos A, B, C y D. Si numéricamente se
cumple 3ABCD = BCAD y BC = 2AB, halle
BD
AB
.
A)
2
1
B)
3
1
C)
5
1
D)
7
1
E)
8
1
Solución:
A B C Da 2a l = 6a
3AB CD = BCAD
3al = 2a(3a + l)
l = 6a
BD
AB
=
8
1
a8
a

Clave: E
2. En la figura, AB = (13 – x2
)m y BC = (6x + 7) m. Halle el mayor valor entero de
AC.
A) 26 B) 27
C) 28 D) 29
E) 30
Solución:
1) AC = 20 + 6x – x2
= 20 – (x – 3)2
+ 9
= 29 – (x – 3)2
Pero (x – 3)2
 0
29 – AC  0
AC  29
ACmax entero = 29
Clave: D
A B C
A B C
13 x 2 6x + 7
Marcos Elantiguo

3. En la figura, ODyOA son opuestos. Halle la suma de los valores máximo y mínimo
entero de x.
A) 105°
B) 106°
C) 107°
D) 100°
E) 96°
Solución:
1) 2x – y + x + y + y – x = 180°
y = 180° – 2a
2) 2x – y > 0
2x > y
2x > 180° – 2x
x > 45°
3) y – x > 0
y > x
180° – 2x > x
60° > x
xmin entero = 46°
xmax entero = 59°
 46° + 59° = 105°
Clave: A
4. Sean los ángulos consecutivos AOB, BOC, COD y DOA tales que
12mBOC = 4mAOB = 3mCOD y 3mDOA = 4mAOB. Halle mAOC.
A) 80° B) 150° C) 130° D) 100° E) 120°
Solución:
3(360° – 8) = 4(3)
 = 30°
mAOC = 4 = 4(30°) = 120°
Clave: E
OA D
C
B
2x y y x
x+ y
A
B
C
D
O
3
4

360° 8 
Marcos Elantiguo

5. Sean los ángulos AOB, BOC y COD se trazan las bisectrices ONyOM de AOB
y COD respectivamente. Si mAOC = 100° y mBOD = 140°, halle mMON.
A) 125° B) 120° C) 130° D) 110° E) 140°
Solución:
1) 140° – 2 = 100° – 2
40° = 2 – 2
20° =  – 
2) x = 140° – 2 +  + 
x = 140° +  – 
x = 140° – 20°
x = 120°
Clave: B
6. Sean los ángulos consecutivos AOB, BOC, COD y DOE donde OCyOB son
bisectrices de AOD y BOE respectivamente. Si 4mCOD = 3mDOE y AOB es
agudo, halle el máximo valor entero de la mCOE.
A) 62° B) 60° C) 70° D) 65° E) 66°
Solución:
 = 7k + 3k = 10k
Pero  < 90°
10k < 90°
k < 9°
7k < 63°
mCOEmax entero = 62°
Clave: A
A
B
C
DM
N
O




100° 2 
x
140° 2 
A
B
C
D
E
O

7k
3k
4k
Marcos Elantiguo

Trigonometría
1. Las medidas de un ángulo positivo  , en los sistemas centesimal y radial, son
g
)10x3(  y rad
x
2
. Calcular la medida de  en el sistema sexagesimal.
A) 36 B) 2,36 C) 4,36 D) 38 E) 35
Solución
0400x30x
x
40
10
30x
x
220
10
30x 2







 



10x0)10x)(40x( 
 3640)3010( gg
Clave: A
2. Las medidas de un ángulo  en los sistemas sexagesimal y centesimal son '930 y
mg
ba respectivamente. Calcular
g
15
ab






en el sistema sexagesimal.
A) 33 B) 99 C) 66 D) 55 E) 22
Solución
mg
ggOO
5033
6
201
9
10
.
20
603
20
603
60
9
30930 











 ' .








 99
10
9
15
5,33
15
ab
g
Clave: B
3. Sean S y g
C las medidas de un ángulo positivo en los sistemas sexagesimal y
centesimal, respectivamente, tal que 231
4C
12C3S4SC



. Hallar la medida
del ángulo en radianes.
A) rad
20
7
B) rad
20
3
C) rad
23
2
D) rad
23
3
E) rad
23
7
Marcos Elantiguo

Solución
Sea 3k27k927S24
4C
)4C)(3S(
24
4C
)4C(3)4C(S






.
Luego, rad
20
3
rad3
20



 .
Clave: B
4. Si 1
5060
30rad
5
2
E g
g




 , hallar el valor de 1E2
 .
A) 4 B) 6 C) 3 D) 1 E) 8
Solución
Sea 31E1
15
45
E1
4560
2772
E 22




Clave: C
5. Sean S , g
C y Rrad las medidas de un ángulo en los sistemas sexagesimal,
centesimal y radial respectivamente. Si
37
R10
S2C3S2C

 , hallar la
medida de dicho ángulo en radianes.
A) rad
60

B) rad
128

C) rad
81

D) rad
5
49

E) rad
5
64

Solución
Tenemos
20
k
R,k10C,k9S

 , entonces 




 


20
k
37
10
)3272(
2
256
kk
16
k)37)(37(4



 .
rad
5
64256
20
R 2









 .
Clave: E
6. Sean S y g
C las medidas de un mismo ángulo en el sistema sexagesimal y
centesimal respectivamente. Hallar la medida del ángulo en radianes
si  32
C
S
C
S
C
S
1 .
A) rad
20

B) rad
10

C) rad
15
2
D) rad
15

E) rad
20
3
Marcos Elantiguo

Solución
1SC
S
1
1
C
1
S
1
C
1
C
1
C
1
S
1
C
S
C
S
C
S
1 3232






 
1k1k9k10 
2020
k
R




Clave A
7. Un ángulo mide S , g
C y Rrad. Si
10
19
CS

 , hallar
R2
2

.
A) 60 B) 100 C) 80 D) 70 E) 200
Solución
i)
10
k
10
19
k10k9
10
19
CS






ii) 100
R2
R200
200102020
k
R
2
2
2









 



Clave: B
8. Un ángulo mide rad
32

y en el sistema sexagesimal '''
debca , donde b y d son
menores que 7. Hallar g
)edcba(  en radianes.
A) rad
12
7
B) rad
100
9
C) rad
19
10
D) rad
9
5
E) rad
79
9
Solución
03735625,5
32
180180
32
rad
32
OO

















.
Luego, 0e,3d,7c,3b,5a  y
rad
100
9
rad
200
18
18)edcba(
gg 





 

Clave: E
Marcos Elantiguo

9. Dos ángulos suplementarios son tales que el número de grados centesimales que
indica la medida de uno de ellos y los dos tercios del número de grados
sexagesimales que indica la medida del otro están en relación de 10 a 9. Calcular la
medida del ángulo mayor en radianes.
A) rad
4
3
B) rad
3
2
C) rad
6
5
D) rad
5
3
E) rad
8
5
Solución
80CC2400C3
9
10
10
9
)C200(
3
2
C


Luego, rad
5
3
rad
2010
120
120)80200( gg 



Clave: D
10. Sean S°, Cg
y Rrad las medidas de un mismo ángulo en los sistemas sexagesimal,
centesimal y radial respectivamente. Si se verifica
,x)x(C10Rx2000Sx100Cx300R2000C300S100 
hallar x .
A) 35 B) 36 C) 37 D) 38 E) 39
Solución
kx)x(100)x(R2000)x(C300)x(S100 
kxR20C3S  , pero
20
k
R,k10C,k9S


Luego, x39kx
20
k
20k30k9kxR20C3S 




 

39x 
Clave: E
EVALUACIÓN Nº 1
1. Con los datos de la figura, hallar el valor de x.
A) 54
B) 68
C) 59
D) 58
E) 61
Marcos Elantiguo

Solución











 
 360
3
200
rad
6
)34x2()4x2(
g
58x232x4360
3
200
10
9
3034x24x2 






Clave: D
2. Al tomar la medida de un ángulo se escribe 'a4 , en lugar de escribir m
a5 ;
cometiéndose un error de '204 . Determinar la medida de dicho ángulo.
A) g
12 B) g
5,12 C) g
7,10 D) g
10 E) g
11
Solución
200a
27
50260
27
a65
a5
27
50260
27
a200
a5204a4
m
mm
m




 ''
gmm
101000a5 
Clave: D
3. Sean S y g
C las medidas de un ángulo en los sistemas sexagesimal y
centesimal respectivamente. Si 4422
C
1
S
1
C
1
S
1
181 





 , hallar la medida de dicho
ángulo en grados centesimales.
A)
g
10
3






B)
g
9
2






C)
g
10
1






D)
g
9
1






E)
g
18
1






Solución
Tenemos ,k10C,k9S  entonces 44
44
22
22
CS
SC
CS
SC
181








 
90
1
k
)100(81
1
kk181k)81)(100(181SCCS181 2242222
 .
g
9
1
90
1
10k10C 











 .
Clave: D
4. Las medidas de los ángulos de un triángulo T son  )3x12( , g
)x1070(  y
rad
5
x





 
. Hallar la medida del menor ángulo de T, en grados centesimales.
A) g
28 B) g
27 C) g
30 D) g
36 E) g
40
Marcos Elantiguo

Solución
x36S
5
x20
9
S
)x963()x1070(
9
S
x7
9
S
10
x1070 g





 



,
luego, 




 
)x36(rad
5
x
.
Luego, 2x114x57180x36)x963()3x12( 
g
3027)3)2(12(menorÁngulo  .
Clave: C
5. El ángulo  mide mg
1515 . Si
2

mide ''' cba con 60bc  )c,b,a( N ,
calcular cba  .
A) 58 B) 32 C) 22 D) 56 E) 35
Solución
68313635,13
10
9
20
303
20
303
1515
g
mg









58cba3496319
2
13
2




 ''''''
Clave: A
Lenguaje
EVALUACIÓN DE CLASE Nº 1
1. Marque la alternativa correcta respecto a la comunicación humana.
A) Se manifiesta solo de forma oral. B) Carece de circunstancia y canal.
C) Puede prescindir del código. D) Consiste en producir sonidos.
E) Puede ser verbal o no verbal.
Clave: E. La comunicación puede ser verbal cuando usamos código lingüístico o no
verbal cuando no usamos código lingüístico.
2. Escriba verdadero (V) o falso (F) con respecto a los siguientes enunciados.
A) En la comunicación verbal, lo esencial es solo la escritura. ( )
B) Las lenguas naturales se expresan únicamente por sonidos. ( )
C) La comunicación se da solo en sociedades humanas. ( )
D) En la comunicación, los interlocutores utilizan el mismo código. ( )
E) La facultad del lenguaje es la base de la comunicación verbal. ( )
Clave: F, F, F, V, V
Marcos Elantiguo

3. A la derecha, escriba la clase de comunicación a la que corresponde cada
enunciado.
A) La Quinta Sinfonía de Beethoven _______________________
B) El semáforo en una avenida _______________________
C) El mensaje enviado por correo _______________________
D) La declamación de un poema _______________________
E) La danza de las abejas africanas _______________________
Clave: A) no verbal acústica, B) no verbal visual, C) verbal escrita, D) verbal oral,
E) no humana
4. En el enunciado ‹‹ayer, Eliana me dijo: ʻTe esperoʼ››, los elementos de la
comunicación resaltados son, respectivamente,
A) oyente y referente. B) emisor y receptor.
C) emisor y referente. D) receptor y referente.
E) emisor y mensaje.
Clave: E. “Eliana” es emisor porque codifica el mensaje y “Te espero” es el mensaje
que envía el emisor al receptor.
5. Seleccione la alternativa que presenta una característica de la lengua.
A) Psicofísica B) Física C) Innata
D) Abstracta E) Momentánea
Clave: D. La lengua es abstracta porque se procesa en la mente/cerebro de los
hablantes.
6. Los procesos psicofísicos de codificación y descodificación son realizados
respectivamente por el
A) receptor y el emisor. B) emisor y el receptor.
C) lector y el escritor. D) oyente y el hablante.
E) interlocutor y el escritor.
Clave: B. Los procesos psicobiológicos de codificación y descodificación son
realizados, respectivamente, por el emisor y el receptor.
7. Cuando el lenguaje cumple la función poética, el elemento de la comunicación
que destaca es el
A) código. B) receptor. C) canal. D) mensaje. E) emisor.
Clave: D. En la función poética, el elemento de la comunicación que destaca es el
mensaje.
Marcos Elantiguo

8. Señale la opción en la que el enunciado cumple la función estética.
A) Me gustan los poemas de Bécquer.
B) Maribel se ha maquillado rápidamente.
C) En ti respiro mucha paz y tranquilidad.
D) La belleza física se desvanece pronto.
E) Los bomberos sí arriesgan sus vidas.
Clave: C. La función es estética porque el elemento que destaca es el mensaje y el
lenguaje empleado es subjetivo.
9. En los enunciados “la palabra holocausto proviene del latín holocaustum” y
“deja la ventana abierta, por favor”, el lenguaje cumple, respectivamente, las
funciones
A) metalingüística y apelativa. B) representativa y emotiva.
C) representativa y estética. D) metalingüística y fática.
E) representativa y fática.
Clave: A. La primera función es metalingüística porque se precisa el código y la
segunda es apelativa porque el elemento que destaca es el receptor.
10. Marque la alternativa en la que aparece el nombre de un sistema de
comunicación verbal escrita.
A) Los gritos de una persona B) El sistema braille
C) Un comentario por Facebook D) Una conversación telefónica
E) Una foto tamaño carné
Clave: C. Un comentario por Facebook es un ejemplo de comunicación verbal
escrita porque se utilizan signos lingüísticos visuales.
11. A la derecha, escriba el nombre que designa a cada concepto.
A) Variedad social de una lengua _____________________
B) Sistema oficial lingüístico _____________________
C) Capacidad innata y universal _____________________
D) Uso del sistema lingüístico _____________________
E) Variedad regional de las lenguas _____________________
Clave: A) sociolecto, B) idioma, C) lenguaje, D) habla, E) dialecto
12. En el enunciado “el ingeniero Ugarte me dijo el viernes por la tarde que las
obras estaban a punto de iniciarse”, el elemento circunstancia es
A) el ingeniero Ugarte. B) las obras.
C) la lengua española. D) me (yo).
E) el viernes por la tarde.
Clave: E. La circunstancia, el día y la hora, es el viernes por la tarde.
Marcos Elantiguo

13. El maullido de los gatos y el siseo de las serpientes constituyen
respectivamente clases de comunicación
A) visual y auditivo. B) auditivo y visual.
C) auditivo y olfativo. D) auditivo y auditivo.
E) táctil y auditivo.
Clave: D. El maullido de los gatos y el siseo de las serpientes son formas de
comunicación auditiva.
14. El lenguaje humano es
A) social. B) innato. C) aprendido.
D) físico. E) momentáneo.
Clave: B. El lenguaje es innato porque forma parte de nuestra condición biológica
como seres humanos.
15. El español hablado por los pobladores de Huanta (Ayacucho) constituye un
dialecto
A) carente de gramática. B) hablado solo por monolingües.
C) de mayor prestigio. D) regional de la lengua española.
E) hablado solo por bilingües.
Clave: D. El dialecto hablado por los pobladores de Huanta es una variación regional
de la lengua española.
16. Cuando Diego felicita oralmente a Roxana diciéndole: “¡Felicidades por tu
beca!”, el código y el canal son respectivamente
A) el aire y Diego. B) Roxana y la felicitación.
C) el español y el aire. D) la felicitación y el papel.
E) visuográfico y el aire.
Clave: C. El código empleado en la comunicación es el español y el canal es el aire.
17. Identifique el enunciado donde destaca la función referencial del lenguaje.
A) Me sorprende ver qué lujoso es el Marriot.
B) Todos, formen grupos de cinco personas.
C) Esta es una fantástica oportunidad para mí.
D) Ernesto está triste porque falleció su líder.
E) El quechua es una lengua andina aglutinante.
Clave: D. En este enunciado, el lenguaje cumple función referencial porque el
elemento que destaca es el referente.
Marcos Elantiguo

18. Elija el enunciado donde el elemento de la comunicación que destaca es el
código.
A) Chomsky dijo: “¿Qué hay en la mente/cerebro?”
B) Respondió a través del “problema de Platón”.
C) La palabra “transgénicos” es esdrújula.
D) Por ti, la verde hierba y la colorada rosa…
E) En la literatura, el amor es un tema frecuente.
Clave: C. El elemento que destaca es el código porque se cumple la función
metalingüística del lenguaje.
19. Escriba el elemento de la comunicación que destaca en cada oración.
A) Los aportes de Chomsky son geniales. ________________
B) ¿Cómo surge el conocimiento en la mente? ________________
C) Aló… ¿Me escucha?... ¿Quién es?, ¿quién es? ________________
D) El cerebro es uno de los centros nerviosos. ________________
E) Un clítico es un elemento gramatical átono. ________________
Clave: A) emisor, B) receptor, C) canal, D) referente, E) código
20. El aviso “Despacio: obras” colocado en una avenida constituye comunicación
A) no verbal visual. B) verbal acústica.
C) audiovisual. D) verbal visuográfica.
E) no verbal visual.
Clave: D. La comunicación constituye comunicación verbal visuográfica porque hay
uso de un código lingüístico constituido por signos visuográficos.
21. Marque el enunciado conceptualmente correcto.
A) La lengua es un sistema de escritura usado por seres vivos.
B) Únicamente las lenguas con más hablantes tienen dialectos.
C) El español del Cusco es la variedad estándar de la región sur.
D) En el Perú, hay solo dos lenguas oficiales: el español y quechua.
E) En las sociedades ágrafas, predomina la comunicación oral.
Clave: E. En las sociedades ágrafas, predomina la comunicación verbal oral.
22. Una figura colocada en un centro de salud para comunicar que se debe
guardar silencio constituye comunicación
A) visuográfica. B) no verbal auditiva. C) no verbal visual.
D) verbal visual. E) verbal gestual.
Clave: C. La comunicación es no verbal visual porque el signo empleado es una
figura.
Marcos Elantiguo

23. ¿Cuál es, entre otras, la intención comunicativa del emisor en la función
apelativa?
A) Informar al receptor. B) Mantener el diálogo.
C) Expresar emociones. D) Precisar el código.
E) Persuadir al receptor.
Clave: E. El emisor busca modificar o persuadir la conducta del receptor dando una
orden, haciendo una pregunta, etc.
24. La descodificación es un proceso psicobiológico que consiste en
A) transmitir el mensaje al receptor.
B) enviar la información a través de signos.
C) captar y entender el mensaje enviado.
D) seleccionar un tema de la realidad.
E) elegir un código para comunicarse.
Clave: C. La descodificación consiste en captar y procesar la información que fue
enviada por el emisor.
25. Marque el enunciado que está expresado en dialecto estándar de la lengua
española.
A) Oye, aguanta el carro que te vas a pasar la luz roja.
B) Señor Ramírez, al toquepala le voy a traer su pedido.
C) Voy a estudiar a forro para aprobar mi primer examen.
D) Lo de nosotros solo fue un choque y fuga y nada más.
E) En serio, ¿es cierto lo que me estás diciendo ahora?
Clave: E. Las demás alternativas deben aparecer de la siguiente manera: A) Espera
un momento que te vas a pasar la luz roja. B) Señor Ramírez, inmediatamente le voy
a traer su pedido. C) Voy a estudiar bastante para aprobar mi primer examen. D) Lo
de nosotros solo fue una relación fugaz.
26. Señale la alternativa donde el enunciado está en dialecto no estándar.
A) De todos modos, es bueno conocer las consecuencias.
B) Informaron que hubieron muchos damnificados en Ica.
C) Frank, un joven con retardo mental, se perdió hace días.
D) Hubo una histeria colectiva en contra de un asesino.
E) Los placebos los usan tanto la medicina como charlatanes.
Clave: B. La oración muestra un lenguaje no estándar y debería ser cambiado por
“Informaron que hubo muchos damnificados en Ica”.
27. Corrija los enunciados expresados en dialecto no estándar.
A) El Mario y la Jenny hicieron click. __________________________
B) No pasa nada con la clase, cuñao. __________________________
C) José cree de que no lo apoyarán. __________________________
D) No les llamé porque no tenía saldo. __________________________
E) La trucha de que comí es sabrosa. __________________________
Marcos Elantiguo

Clave: A) Mario y Jenny se enamoraron rápidamente. B) La clase no cumple con las
expectativas, amigo. C) José cree que no lo apoyarán. D) No los/las llamé porque no
tenía saldo. E) La trucha que comí era sabrosa.
28. Marque el enunciado que está expresado en dialecto estándar.
A) El pequeño Diego padece de un transtorno de conducta.
B) Subiremos por el ascensor al treceavo piso del edificio.
C) Víctor se irrogó atribuciones que no le correspondían.
D) Ellos lavaron todos los pantalones y las camisas sucias.
E) La primera alumna del salón es procedente de la selva.
Clave: E. A) trastorno, B) decimotercer, C) se arrogó, D) sucios.
29. Marque el enunciado en la que hay empleo correcto de la expresión subrayada.
A) Ahora tiene un sin fín de temas por estudiar.
B) A él le gustó la película Una historia sinfín.
C) En la oficina, hay un sinfín de expedientes.
D) Nuestro universo es un espacio sinfín.
E) Por un sin fín de problemas se suicidó.
Clave: C. Se escribe sinfín junto porque es un sustantivo.
30. Identifique el enunciado donde hay precisión léxica del término subrayado.
A) Lucy se siente en la sima del mundo por su éxito.
B) Se ha cometido una inequidad bastante grande.
C) Hay un dominio eminente de su partido político.
D) Aquel grupo de adolescentes realizó un delito.
E) El aceite es una sustancia insalubre en el agua.
Clave: C. A) cima, B) iniquidad, D) perpetró, E) insoluble
Literatura
EJERCICIOS DE CLASE
1. El género lírico se caracteriza por ser subjetivo debido a que el autor
A) representa movimientos y sentimientos.
B) crea la ilusión de la impersonalidad.
C) muestra el diálogo y las acciones.
D) se expresa desde su mundo interior.
E) alude a sucesos del tiempo pasado.
Solución:
Respecto a otros géneros literarios, el género lírico tiene como característica el ser
de índole subjetiva, ya que el autor se expresa desde su mundo interior.
Clave: D
Marcos Elantiguo

2. ¿Por qué este fragmento de Cien años de soledad, de Gabriel García Márquez
pertenece al género épico?
“Todos los años, por el mes de marzo, una familia de gitanos desarrapados plantaba
su carpa cerca de la aldea, y con un grande alboroto de pitos y timbales daban a
conocer los nuevos inventos. Primero llevaron el imán. Un gitano corpulento, de
barba montaraz y manos de gorrión, que se presentó con el nombre de Melquíades
[…]”.
A) Refleja la experiencia muy personal del narrador.
B) Narra, describe ambientes y retrata a un personaje.
C) Representa las hazañas del gitano Melquiades.
D) Comenta de forma subjetiva un suceso del pasado.
E) Predomina el diálogo y movimiento del personaje.
Solución:
En este fragmento el autor alterna la descripción de Macondo con el retrato físico del
gitano Melquiades, por lo tanto pertenece al género épico. Este género se
caracteriza por alternar descripciones de lugares, objetos, retratar personajes y,
sobre todo, por la objetividad que posee el autor para narrar.
Clave: B
3. ¿Cuál es la figura literaria presente en los siguientes versos del poeta mexicano
Octavio Paz?
Las palabras, guantes grises, polvo mental sobre la yerba, el agua, la piel;
A) Hipérbaton B) Anáfora C) Hipérbole
D) Metáfora E) Epíteto
Solución:
La metáfora se construye por la sustitución del elemento “palabra” con “guantes
grises” y “polvo mental”.
Clave: D
4. Marque la alternativa que contiene la figura literaria empleada en el siguiente
fragmento de la “Égloga III”, de Garcilaso de la Vega.
Cerca del Tajo, en soledad amena,
de verdes sauces hay una espesura
A) Metáfora B) Hipérbole C) Hipérbaton
D) Anáfora E) Símil
Solución:
Se ha producido un hipérbaton en la expresión: “Hay una espesura de verdes sauces
cerca del Tajo en soledad amena”.
Clave: C
Marcos Elantiguo

5. Marque la alternativa que completa adecuadamente el siguiente enunciado sobre la
Ilíada, de Homero: “Se trata de una obra épica, cuya especie se denomina______;
está compuesta por veinticuatro___________ escritos en hexámetros”.
A) epopeya – cantos B) cantar de gesta – estrofas
C) poema épico – capítulos D) novela – episodios
E) crónica – secciones
Solución:
La Ilíada es una obra épica de la especie denominada epopeya; se encuentra
dividida en veinticuatro cantos o rapsodias escritas en hexámetros.
Clave: A
6. Con respecto a la verdad (V) o falsedad (F) de los siguientes enunciados sobre el
argumento de la Ilíada, de Homero, marque la alternativa que contiene la secuencia
correcta.
I. En el noveno año de guerra Aquiles abandona el campo de batalla.
II. Homero describe minuciosamente el rapto de Helena por Paris.
III. Aquiles vuelve a la batalla con el deseo de vengarse de Héctor.
IV. En la obra los dioses intervienen en la guerra de los mortales.
V. El padre de Héctor suplica le devuelvan el cadáver de su hijo.
A) VFFFV B) FFVVV C) FFFVV D) FVFVF E) VFFVV
Solución:
I. En el décimo año de guerra se desata la cólera de Aquiles abandona la batalla por
la afrenta que le hace Agamenón (F). II. Homero narra la cólera de Aquiles y sus
funestas consecuencias. (F). III. Debido a la muerte de Patrocolo, Aquiles vuelve a
combatir para vengarse de Héctor (V). IV. Los dioses intervienen favoreciendo según
los bandos en pugna. (V). V. El padre de Héctor, el rey Príamo, le suplica a Aquiles
para que le devuelva el cadáver de su hijo Héctor. (V)
Clave: B
7. En la Ilíada, de Homero, el destino del hombre
A) causa la destrucción de la ciudad de Troya.
B) origina que estos luchen para poder revertirlo.
C) es semejante al de los dioses del Olimpo.
D) aparece ligado al destino de su patria.
E) está sometido a la voluntad de los dioses.
Solución:
Homero, en la Ilíada, de Homero, los dioses intervienen constantemente en la vida
de los hombres y determinan el curso de su existencia.
Clave: E
8. Seleccione la alternativa que completa el siguiente enunciado sobre la Odisea, de
Homero: “El deseo constante del héroe por volver a Ítaca da cuenta de uno de los
temas principales del texto: ____________”.
A) la lucha humana B) el destino inevitable C) el amor a la patria
D) la astucia del héroe E) el afán por el poder
Marcos Elantiguo

Solución:
El deseo constante del héroe por volver a Ítaca da cuenta de uno de los temas
principales del texto: el amor a la patria.
Clave: C
9. ¿Cuál de los siguientes eventos ocurre en la epopeya Odisea, de Homero?
A) Odiseo ingiere la flor de loto y naufraga en la isla de Ogigia.
B) Penélope y Telémaco planean acabar con los pretendientes.
C) Poseidón hace que naufrague en el país de los Cíclopes.
D) Odiseo, gracias a la ayuda de su hijo, logra armar el arco.
E) Calipso, aconsejada por Atenea, deja partir a Odiseo.
Solución:
En la isla de Ogigia, Odiseo ha vivido durante siete años con la diosa Calipso;
gracias a la intervención de Atenea, quien es enviada por Zeus, aconseja a Calipso
liberar al héroe.
Clave: E
10. En Ilíada y Odisea subyace la idea de la vida; en la primera se trata de una
________ constante para alcanzar la dignidad; mientras que en la segunda, la vida
es un viaje________ que se debe afrontar para realizar el destino personal.
A) fantasía – corto B) duda – enigmático
C) celebración – extraño D) lucha – difícil
E) negociación – complicado
Solución:
En la Ilíada, la vida es una lucha constante para alcanzar la dignidad; mientras que
en la Odisea, es un viaje difícil que se debe afrontar para realizar el destino personal.
Clave: D
Psicología
PRÁCTICA Nº 01
Instrucciones: Leer detenidamente cada pregunta y elegir la respuesta que se estime
verdadera.
1. La relación que hay entre la actividad mental y la adaptación del individuo a su
entorno fue el objeto de estudio de la escuela
A) conductista. B) psicoanalítica. C) cognitivista.
D) estructuralista. E) funcionalista.
Solución:
El objeto de estudio del Funcionalismo fue la función de la conciencia, cómo estudiar
el tema de la adaptación de las personas ante determinadas situaciones o
ambientes.
Rpta.: E.
Marcos Elantiguo

2. La aplicación de un método mnemotécnico y sus efectos en la retención de una
lectura en estudiantes, corresponde a una investigación de tipo
A) correlacional. B) descriptivo. C) experimental.
D) intuitivo. E) deductivo.
Solución:
El método experimental trabaja con dos tipos de variables: Variable independiente
(V.I.) y Variable dependiente (V.D.). La V.I. es causal y es manipulada por el
experimentador para probar sus efectos sobre la V.D. La V.D. se mide para ver los
cambios que produce la manipulación de la V.I.
Rpta.: C.
3. La evaluación y selección de un grupo de mineros que postula a una plaza de alta
exigencia en su área, está a cargo del psicólogo
A) educativa. B) organizacional. C) psicosocial.
D) social. E) clínica.
Solución:
La psicología organizacional se interesa en los procesos de selección, motivación y
capacitación del personal, desarrollo organizacional y mejoramiento del clima
institucional, entre otros. Trabajan en empresas, financieras y organizaciones en
general.
Rpta.: B.
4. Benjamín padece de acrofobia (pánico a las alturas) y está acudiendo a un
tratamiento psicológico para superarlo. Este sería un caso propio de la especialidad
psicológica denominada
A) educativa. B) jurídica. C) clínica.
D) social. E) organizacional.
Solución:
La psicología clínica está dirigida al diagnóstico y tratamiento de los desórdenes
conductuales o emocionales. Los psicólogos clínicos trabajan en hospitales, clínicas,
consultorios privados, entre otros.
Rpta.: C
5. En algunas tribus de a África las mujeres cargan unos aros en el cuello que permiten
hacerlo más largo, lo cual las hace sentirse más bellas, distinguidas y valoradas por
la tribu. Este caso forma parte del campo de estudio de la psicología
A) social. B) organizacional. C) psicosocial.
D) educativa. E) clínica.
Solución:
La psicología social se interesa cómo el contexto socio-cultural afecta la conducta de
los individuos, los procesos grupales, los roles sociales, formación y cambio de
actitudes, entre otros. Igualmente desarrolla proyectos preventivos y de promoción
psicosocial.
Rpta.: A.
Marcos Elantiguo

6. La explicación de que la depresión, entre otros aspectos, está asociada a un
desbalance de determinados neurotransmisores es propia del enfoque
A) biopsicológico. B) conductista. C) psicodinámico.
D) cognitivista. E) humanista.
Solución:
El enfoque biopsicológico explica el comportamiento desde la perspectiva del
funcionamiento biológico.
Rpta.: A
7. La afirmación “Los estímulos son los que determinan y controlan la conducta del
hombre” es compatible con el enfoque psicológico
A) humanista. B) conductista. C) estructuralista.
D) psicoanalítico. E) cognitivista.
Solución:
El enfoque conductista afirma que el comportamiento se encuentra controlado por las
contingencias de la respuestas con los estímulos; el ambiente es aquel que
condiciona la conducta.
Rpta.: B.
8. Clara está siendo sometida a una serie de pruebas psicológicas para determinar su
vocación profesional y en consecuencia elija una carrera universitaria. Esta labor es
propia del psicólogo
A) organizacional. B) laboral. C) social.
D) clínico. E) educativo.
Solución:
El psicólogo educativo se encarga de aspectos del proceso enseñanza, problemas
de aprendizaje y conducta, temas de desarrollo y estimulación temprana, orientación
vocacional, entre otros. Laboran en instituciones educativas y centros privados.
Rpta.: E.
9. Un aprendiz de violín que práctica constantemente con su instrumento tocando
siempre la misma melodía debido a que recibe elogios en público. El enfoque
utilizado para explicar este comportamiento es el
A) estructuralista. B) psicoanalítica. C) conductista.
D) cognitivista. E) funcionalista.
Solución:
El enfoque conductista estudia respuestas manifiestas u observables, las cuales se
encuentran sujetas a los estímulos reforzadores, con en este caso, los elogios en
público.
Rpta.: C.
Marcos Elantiguo

10. La expresión “Cada hombre es lo que hace con lo que hicieron de él” correspondería
a una perspectiva psicológica compatible con el enfoque
A) psicodinámico. B) humanista. C) conductual.
D) cognitivo. E) estructuralista.
Solución:
El enfoque humanista destaca la importancia del libre albedrio en el ser humano;
por tanto, es más trascendente la actitud que asume la persona ante una experiencia
que la experiencia en sí misma, por muy adversa que ésta haya sido.
Rpta.: B.
Historia
EVALUACIÓN DE CLASE Nº 1
1. La historia es una ciencia que tiene como objeto de estudio
A) predecir los acontecimientos humanos del futuro únicamente.
B) investigar el desarrollo de las sociedades en el tiempo y el espacio.*
C) relatar amenamente los hechos de los grandes personajes.
D) analizar la evolución física humana por diversos territorios.
E) imaginar los acontecimientos humanos de carácter político.
“B” La historia es una ciencia de carácter social que tiene como objeto de estudio al
hombre como ser social. Su objetivo principal es investigar los hechos históricos en
sus causas, desarrollos y consecuencias, en un determinado tiempo y espacio.
2. Fue una característica económica del Paleolítico.
A) Surgimiento de la agricultura. B) Desarrollo de la vida aldeana.
C) Predominio de la depredación.* D) Organizado en sistema de clanes.
E) Decadencia de las bandas.
“C” Durante el período Paleolítico la sociedad humana practicó una economía de
subsistencia, depredaba la naturaleza mediante la caza, la pesca y la recolección de
vegetales. La gente cazaba en grupo y compartía los alimentos.
3. Identifique el proceso que corresponde al Mesolítico.
A) Invención de la metalurgia. B) Iniciación de la horticultura.*
C) Expansión de las aldeas. D) Organización social en tribus.
E) Consolidación de las jefaturas.
“B” El Mesolítico es el tránsito de la piedra tallada a la piedra pulida, pero también
es el paso de una economía depredadora a otra más bien productiva. En ese tiempo
se inicia la horticultura con la domesticación de las primeras plantas.
Marcos Elantiguo

4. Con relación al período Neolítico se llevó a cabo la
A) producción de alimentos.* B) expansión de la esclavitud.
C) acuñación de monedas. D) aparición de ciudades.
E) invención de la escritura.
“A” En el Neolítico el hombre perfecciona la domesticación de plantas -destacando los
cereales como el trigo y la cebada- y animales -como cabras, ovejas y asnos-
produciéndose la “Revolución neolítica”, planteada por el arqueólogo australiano
Gordon Childe, al desarrollarse la agricultura y ganadería que significarían para los
hombres un cambio radical de sus costumbres en base a una economía productora.
5. Fue un aspecto político de la Edad del bronce.
A) Inicio de los gobiernos jefaturales.
B) Crisis de monarquías aldeanas.
C) Predominio de clanes guerreros.
D) Surgimiento de imperios militaristas.*
E) Decadencia de los estados esclavistas.
“D” Durante la Edad del bronce aparecerán los primeros estados del Creciente Fértil
como Egipto y Mesopotamia. En el caso de Mesopotamia se desarrollarán las
ciudades-Estado sumerias que en algunos casos se expandirán militarmente. Los
primeros imperios (estados expansivos) aparecen en este período como es el caso
de Acadia, Asiria y Babilonia en Mesopotamia y Egipto donde la esclavitud fue cada
vez más importante.
Geografía
EJERCICIOS Nº 1
1. A mediados del XIX, la Geografía se institucionaliza en la universidad alemana,
donde vivieron __________________ que propiciaron el desarrollo del pensamiento
geográfico _________________.
A) Vidal de la Blache y William Davis – radical
B) los enciclopedistas – posibilista
C) Humboldt y Ritter – moderno
D) Ratzel y Mackinder – crítico
E) Max Sorre y De Martonne – descriptivo
Solución:
A mediados del XIX, la Geografía está institucionalizada en la Universidad y es curso
en las enseñanzas primarias y medias. Este escenario comienza en Alemania, donde
vivieron A. Humboldt (1769-1859) y Carl Ritter (1779-1859), y son considerados los
padres del pensamiento geográfico moderno.
Clave: C
Marcos Elantiguo

2. Es el conjunto de entidades bióticas, abióticas, y antrópicas en permanente
interrelación que origina cambios cualitativos y cuantitativos de nuestro planeta.
A) Geosistema B) Espacio geográfico C) Biosfera
D) Ecosistema E) Ecorregión
Solución:
El geosistema, es una unidad funcional, es el conjunto de entidades bióticas,
abióticas y antrópicas, entre las cuales se producen permanentes interrelaciones
que originan cambios cualitativos y cuantitativos que caracterizan finalmente la
estructura terrestre.
Clave: A
3. Entre el eje terrestre y ______________________ la distancia angular
correspondiente es de _______________.
A) la perpendicular a la eclíptica - 66°33’ B) el plano de la eclíptica – 66°33’
C) el polo magnético – 23°27’ D) el trópico de Cáncer – 90°00’
E) el círculo mayor – 180°00’
Solución:
Entre el plano de la eclíptica y el eje terrestre hay aproximadamente 66°33’ de
distancia angular. Esta inclinación más el movimiento de traslación genera sucesión
de las estaciones del año.
Clave: B
4. Acerca del círculo máximo de la Tierra es correcto afirmar que
A) divide la Tierra en hemisferios Oeste y Este.
B) origina una zona de gran contraste térmico.
C) allí la radiación solar incide tangencialmente.
D) le corresponde mayor achatamiento ecuatorial.
E) es el plano perpendicular al eje terrestre.
Solución:
El círculo máximo es el plano perpendicular al eje terrestre que pasa por su centro.
El ecuador divide la Tierra en dos hemisferios: Norte y Sur. El círculo ecuatorial de la
Tierra mide unos 40.075 km (1° equivale aproximadamente a 111,3 km).
Clave: E
5. Sudamérica se localiza en el hemisferio ____________ tomando como referencia el
meridiano de Greenwich.
A) Poniente B) Levante C) Septentrional
D) Austral E) Boreal
Solución:
El meridiano base de Greenwich divide a la Tierra en los hemisferios occidental o
poniente y hemisferio oriental o levante.
Clave: A
Marcos Elantiguo

6. Las principales líneas imaginarias atraviesan el continente
A) americano. B) asiático. C) africano.
D) europeo. E) oceánico.
Solución:
Los trópicos de Cáncer y Capricornio, así como la línea ecuatorial y el meridiano
base de Greenwich cruza imaginariamente el continente africano.
Clave: C
7. El país sudamericano que se encuentra en la trayectoria del trópico de Capricornio es
A) Surinam. B) Ecuador. C) Bolivia.
D) Uruguay. E) Brasil.
Solución:
El trópico de capricornio se localiza aproximadamente a 23°27’ de L.S. en su
trayectoria recorre los países sudamericanos como: Chile, Argentina, Paraguay y
Brasil.
Clave: E
8. Es la distancia angular medida desde la línea ecuatorial hasta un punto del globo
terráqueo.
A) Coordenada B) Paralelos C) Longitud
D) Latitud E) Altitud
Solución:
La latitud es la distancia angular desde el Ecuador terrestre a cualquier punto del
globo terráqueo. La distancia angular máxima es 90°.
Clave: D
9. Halla la diferencia de latitudes y longitudes, respectivamente, entre las ciudades A y
B, las cuales tienen las siguientes coordenadas geográficas: A) 43°LN y 110°LW, y
B) 27° LS y 45° LW.
A) 60°y 65° B) 66° y 165° C) 63°y 155°
D) 70° y 65° E) 70° y 155°
Solución:
• Hallamos la diferencia de latitudes de las ciudades A y B. Si dos lugares de
interés se encuentran en diferentes hemisferios, se debe realizar una suma:
43°LN – 27°LS = 70°
• Hallamos la diferencia de longitudes de las ciudades A y B. Si dos lugares de
interés se encuentran en diferentes hemisferios, se debe sumar los grados:
110°LW – 45°LW = 65°
Clave: D
Marcos Elantiguo

10. ¿Cuáles son las coordenadas geográficas del punto “A”?
A) 60° LS y 95º LE B) 95° LN y 60° LS C) 60° LN y 95º LW
D) 95° LW y 110° LE E) 155° LS y 60° LW
Solución:
El punto A, por ubicarse por debajo de la línea ecuatorial, tiene una latitud sur de 60°
y por ubicarse a la derecha del meridiano de Greenwich, tiene una longitud este de
95°.
Clave: A
Filosofía
EVALUACIÓN N° 01
1. Acerca de la actitud filosófica, es correcto afirmar que
I. la filosofía es un conocimiento absolutamente verdadero.
II. el típico filósofo es radical y crítico.
III. una teoría filosófica nunca cuestiona el orden establecido.
A) I y II B) I y III C) II D) III E) II y III
Solución:
Todo filósofo se caracteriza por cuestionar las verdades, teorías o ideologías
establecidas.
Clave: C
2. Relaciona acertadamente cada disciplina filosófica con su respectivo objeto de
estudio.
1. Ontología a. la moral
2. Ética b. el ser
3. Epistemología c. los valores
4. Axiología d. la ciencia
A) 1a - 2d - 3b - 4c B) 1d - 2c - 3b - 4a C) 1c - 2d - 3a - 1b
D) 1b - 2a - 3d - 4c E) 1d - 2b - 3a - 4c
Solución:
La ontología estudia el último presupuesto existente, el ser de todas las cosas, la
ética reflexiona sobre los problemas morales, la epistemología investiga el
conocimiento científico o ciencia y la axiología examina los valores humanos.
Clave: D
0°
A
0°
40°
50°
60°
70°
85° 90° 95° 100° 105°110°
Marcos Elantiguo

3. Es un concepto enraizado con la filosofía del periodo pre-socrático.
A) Virtud B) Mayeútica C) Dios
D) Caos E) Arjé
Solución:
Los filósofos presocráticos o cosmólogos trataban de hallar un principio o arjé de
todas las cosas.
Clave: E
4. Heráclito fue un filósofo griego cuyas teorías tienen un fundamento
A) poético. B) mitológico. C) material.
D) ideal. E) social.
Solución:
Para Heráclito, el fundamento de todas las cosas es el fuego, o sea, un elemento
material.
Clave: C
5. Los sofistas, fueron un movimiento de sabios y pedagogos, cuyo tema central son los
problemas
A) humanos. B) artísticos. C) laborales.
D) religiosos. E) matemáticos.
Solución:
Los sofistas pertenecen al periodo antropológico de la filosofía antigua, en virtud de
lo cual se ocuparan de los problemas humanos como la vida en la polis, la moral.
Clave: A
6. Identifica la secuencia exacta de verdades (V) y falsedades (F) sobre los sofistas y
Sócrates.
I. Para Protágoras todas las personas y pueblos tienen la misma norma moral. ( )
II. Sócrates dijo que sabiduría hace bueno al hombre. ( )
III. Gorgías afirmó que el origen de todo es un elemento cósmico. ( )
A) VVV B) FFV C) FVF D) VFV E) VFF
Solución:
Protágoras es relativista, para él no existe una norma moral universal, Sócrates, dijo,
efectivamente, que la sabiduría conduce al bien, a la virtud, y, las ideas de Gorgías
no pertenecen al contexto de la filosofía pre-socrática, su tema central es el
conocimiento.
Clave: C
7. Una de las siguientes proposiciones expresa la diferencia entre el mito y la filosofía:
A) El mito es un conocimiento exacto mientras que la filosofía es inexacta.
B) La filosofía representa la realidad vía conceptos; los mitos vía fantasmagorías.
C) Hesiodo elaboró teorías filosóficas, pero Thales ideó mitologías.
D) La mitología tiene más poder explicativo que la filosofía.
E) La filosofía y la mitología difieren solamente en la forma.
Marcos Elantiguo

Solución:
La filosofía es un conocimiento conceptual mientras que la mitología es un
conocimiento fantástico de la realidad.
Clave: B
8. Aristóteles define a la filosofía como una ____________ mientras que Wittgenstein la
define como una _____________.
A) ciencia – actividad B) experiencia – verdad
C) cosmovisión – concepción D) subjetividad – objetividad
E) esperanza – fe
Solución:
La definición aristotélica de filosofía pone de relieve a la ciencia, en cambio,
Wittgenstein la considera como una actividad de esclarecimiento lógico del lenguaje.
Clave: A
9. La corrupción en todos los ámbitos, las violaciones a los derechos humanos son
problemas que merecen la orientación de la disciplina filosófica denominada
A) Ontología. B) Epistemología. C) Ética.
D) Psicología. E) Gnoseología.
Solución:
La Ética, contribuye a una reflexión crítica sobre las acciones justas o injustas que
realizan los individuos.
Clave: C
10. Cuando decimos que la mayeútica es semejante a un método de enseñanza que
trata de extraer las verdades que subyacen en la conciencia del discípulo, nos
referimos a
A) Heráclito. B) Protágoras. C) Anaximandro.
D) Gorgias. E) Sócrates.
Solución:
Toda referencia a la mayeútica está relacionada con Sócrates.
Clave: E
Marcos Elantiguo

Física
Nota: Los ejercicios en (*) corresponden a las áreas B, C y F.
Los ejercicios 3, 7, 11 y 17 son tareas para la casa.
1. (*) Indique la verdad (V) o falsedad (F) de las proposiciones.
I) Si dos cantidades físicas tienen la misma dimensión, entonces necesariamente
son iguales.
II) Todos los términos de una ecuación física no necesariamente tienen las mismas
dimensiones.
III) Solo se pueden sumar o restar cantidades físicas de la misma dimensión.
A) VVV B) VVF C) FVF D) FVV E) FFV
Solución:
I) F II) F III) V
Rpta: E
2. (*) Halle la dimensión de n, si la ecuación n =
tv3
MR
3
es dimensionalmente correcta,
donde R: radio, M: masa, t: tiempo y v: volumen.
A) MT–1
B) ML–1
C) ML–1
T–1
D) MLT–2
E) ML–2
T
Solución:
n =
TL
ML
3
3
= MT
–1
Rpta: A
3. (*) Si la expresión F =
cb
a
2
vt
t
m








es dimensionalmente correcta donde m: masa,
t: tiempo, v: velocidad y F: fuerza, determine a + b + c.
A) 5 B) 4 C) 3 D) 2 E) 1
Solución:
MLT
–2
=
a2
a
t
M
· c1b
)LT(T 
= ccba2a
TLTM

MLT
–2
= ccba2a
LTM

Luego a = 1, c = 1, – 2a + b – c = – 2  b = 1
y a + b + c = 1 + 1 + 1 = 3
Rpta: C
Marcos Elantiguo

4. (*) En la ecuación dimensionalmente correcta, h =
g
v
x
donde g: aceleración,
h: altura y v: velocidad, determine el valor de x.
A) 2 B) 1 C)
2
1
D)
2
3
E) – 1
Solución:
h =
g
v
x
 h g = v
x
L(LT
–2
) = (LT
–1
)
x
L
2
T
–2
= L
x
T
–x
x = 2
Rpta: A
5. (*) Indicar la verdad (V) o falsedad (F) de las siguientes proposiciones:
I. El peso y la masa no tienen la misma dimensión.
II. Dos cantidades físicas diferentes pueden tener dimensiones iguales.
III. Dos cantidades físicas que se suman o restan deben tener las mismas
dimensiones.
A) FVV B) FFV C) VVV D) FFF E) VFF
Solución:
I) V II) V III) V
Rpta: C
6. (*) De los vectores mostrados en la figura, determine la magnitud del vector
resultante R = A + B + C + D. R = A +B +C + D .
A) 1 cm
B) 2 cm
C) 4 cm
D) 5 cm
E) 6 cm
Marcos Elantiguo

Solución:
R = 2 cm
Rpta: B
7. (*) La figura muestra la dirección de los vectores A y B y el eje X; según esto, la
magnitud de A + B será
A) 148
B) 100
C) 196
D) 96
E) 48
Solución:
R = 60cos)6)(8(268
22

= 483664  = 148
Rpta: A
Marcos Elantiguo

8. (*) Calcule la magnitud de la resultante de los vectores A , B y C mostrados en la
figura, sabiendo que A = 8 u, B = 3 u y C = 5 u.  PQOP 
A) 9 u
B) 8 u
C) 6 u
D) 11 u
E) 12 u
Solución:
R = CBA  = 9 u
Rpta: A
9. En la ecuación dimensionalmente homogénea v = Fx
y
, donde v: velocidad,
F: fuerza, : masa/longitud, calcule los valores de x e y respectivamente.
A) – 1/2, – 1/2 B) – 1/2, 1/2 C) 1/2, 1/2 D)
1/2, – 1/2 E) 1, – 1
Solución:
     x y
v F 
   
x y
1 2 1 x y x y 2x
LT MLT ML M L T     
 
–2x = – 1, x – y = 1
1
x
2
 ,
1
y
2
 
Clave: D
Marcos Elantiguo

10. Dada la ecuación dimensionalmente homogénea
x
v sen
R
a

 , donde R: distancia,
v: velocidad y a: aceleración, calcule el valor de x.
A) 1 B) 2 C) 3 D) 4 E) 5
Solución:
 
 
 
x
v
R
a

1 x x x
x 1 x 2
2 2
(LT ) L T
L L T
LT LT
 
  
 
  
x = 2
Clave: B
11. La ecuación P = Dx
ay
tz
es dimensionalmente correcta. Calcule x + y + z, donde
P: presión, D: densidad, a: aceleración y t: tiempo.
A) 5 B) 3 C) 8 D) 7 E) 6
Solución:
       x y z
P D a t →    
x y
1 2 3 2 z
ML T ML LT T   

1 2 x 3x y 2y z
ML T M L T     

x 1 ; 3x y 1    ; 2y z 2   
x 1 ; y 2 ; z 2 → x y z 5  
Clave: A
12. Dada la ecuación dimensionalmente correcta 3
x
b
kxF  donde x: distancia, F:
fuerza, determine la dimensión de b.
A) ML–2
T B) MT–2
C) M–1
LT D) ML4
T–2
E) MLT
Solución:
 
 
3
b
F
x

 
 
→     3
b F x
    2 3 4 2
b MLT L ML T 
 
Clave: C
Marcos Elantiguo

13. En la figura, determine la magnitud de la resultante de los vectores mostrados.
A) 4 cm
B) 2 2 cm
C) 3 2 cm
D) 7 cm
E) 5 cm
Solución:
De la gráfica:
R = 4 cm
Rpta: A
14. Para los vectores que se muestran en la figura, la magnitud del vector resultante
R = A + B + C + D es
A) 2 2 u
B) 3 2 u
C) 3 u
D) 4 2 u
E) 2 3 u
Solución:
R = 22
22  = 8 = 2 2 u
Rpta: A
Marcos Elantiguo

6 u
4 u 2 u
A
B
C
15. Dados los vectores mostrados en la figura, determine la magnitud del vector
A + B2 + C2 .
A) 6 cm
B) 7 cm
C) 8 cm
D) 12 cm
E) 10 cm
Solución:
R = 6 cm
Clave: A
16. En el cuadrado mostrado en la figura, calcule la magnitud del vector
A – B + 2C .
A) 12 u
B) 8 u
C) 10 u
D) 24 u
E) 30 u
Solución:
Clave: C
Marcos Elantiguo

A
M B
120°
2u
1u
M
2u
2u
120°
120°
60°
1u
120°
2 + 2 = 4u
17. En la figura, calcule la magnitud de la resultante de los vectores mostrados en el
rombo de lado 2 u, siendo M punto medio del lado.
A) 21 u
B) 21 u
C) 10 u
D) 10 u
E) 20 u
Solución:
  2 2
R 1 4 2 1 4 cos60   
   R 1 16 2 1 4 1/ 2  
R 21 u
Clave: B
Química
SEMANA Nº 1: LA QUÍMICA COMO CIENCIA NATURAL – MAGNITUDES Y
UNIDADES SI. CONVERSIONES. NOTACIÓN CIENTÍFICA.
1. Sobre la base de los siguientes estudios realizados, ¿cuál de las siguientes
proposiciones responde a una ley científica?
A) La relatividad de Einstein. B) La extinción de los dinosaurios.
C) La evolución de Darwin. D) El Big Bang.
E) La gravitación universal.
Marcos Elantiguo

Solución
La gravitación universal responde a una ley científica: “la fuerza de atracción que
experimentan dos cuerpos dotados de masa es directamente proporcional al
producto de sus masas e inversamente proporcional al cuadrado de la distancia que
los separa”.
Las demás proposiciones responden a teorías.
Rpta: E
*2. De las siguientes magnitudes indique las que son básicas en el SI.
a) tiempo b) intensidad de corriente c) fuerza
d) densidad e) cantidad de sustancia f) presión
A) c, d, f B) a, b, c, C) a, b, e D) a, b, d E) b, c, d
Solución
magnitud Tipo de magnitud
a) tiempo básica
b) intensidad de corriente básica
c) fuerza derivada
d) densidad derivada
e) cantidad de sustancia básica
f) presión derivada
Rpta: C
*3. Establecer la correspondencia entre prefijo y factor
a) tera ( ) 106
b) kilo ( ) 10–12
c) mega ( ) 10–6
d) pico ( ) 103
e) micro ( ) 1012
A) c, d, e, b, a B) c, d, e, a, b C) a, b, d, e , c
D) a, b, d, c, e E) a, b, c, d, e
Solución
a) tera ( c ) 106
b) kilo ( d ) 10–12
c) mega ( e ) 10–6
d) pico ( b ) 103
e) micro ( a ) 1012
Rpta: A
*4. Indique la secuencia correcta de verdadero (V) o falso (F) con respecto a las
siguientes equivalencias:
I) 6,2 x 10 –9
m = 6,2 nm
II) 3,0 x 10 –1
kg = 3,0 dg
III) 7,8 x 10 9
s = 7,8 Gs
A) FVV B) VVF C) VVV D) VFV E) FVF
Marcos Elantiguo

Solución
Rpta: D
5. La masas de 3 barras de acero fueron expresadas de la siguiente forma:
a) 6,45 x 1012
pg b) 2,48 x 1010
ng c) 1,23 x 10–2
kg
Ordénelas de mayor a menor masa
A) a, b, c B) c, b, a C) c, a, b D) b, a, c E) b, c, a
Solución
Luego: masa b > masa c > masa a
Rpta: E
*6. La temperatura de fusión del aluminio es de 660 ºC. Exprese dicha temperatura en
ºF y R respectivamente:
A) 1156 ; 760 B) 1220 ; 1680 C) 1156 ; 1680
D) 1220 ; 760 E) 1220 ; 1156
Solución
Rpta: B
Marcos Elantiguo

7. Una muestra de carbón es calentada desde 50 ºC hasta 150 ºC. ¿Cuál es el
incremento de temperatura en R?
A) 100 B) 180 C) 108 D) 150 E) 190
Solución
Δ ºC = 150 - 50 = 100 ºC
Como: 1 K = 1 ºC = 1,8 ºF = 1,8 R
Entonces: Δ 100 ºC = Δ 180 R
Rpta: B
*8. En un tubo de neón, este gas alcanza una presión aproximada de 1,5 atm. Exprese
la presión en mmHg y Pa respectivamente.
(1 atm = 1,01 x 105
Pa = 760 mmHg)
A) 1,14 x 103
; 1,51 x 105
B) 1,51 x 105
; 1,14 x 10 –3
C) 1,14 x 105
; 1,51 x 103
D) 1,14 x 103
; 1,51 x 10–5
E) 1,14 x 10–3
; 1,51 x 105
Solución
Rpta: A
9. Bajo ciertas condiciones la densidad del amoniaco gaseoso es 0,63 g/L. ¿Cuál es la
masa, en kg, de amoniaco contenido en un recipiente cuyo volumen es 5,0 m3
?
A) 6,30 x 103
B) 6,30 x 101
C) 3,15 x 100
D) 3,15 x 10–3
E) 2,26 x 103
Solución
Rpta: C
10. Calcular la masa, en unidades SI, de un cubo de plomo de 2 dm de arista, cuya
densidad es de 11,4 g/ cm3
.
A) 9,12 x102
B) 9,12 x101
C) 9,12 x10–1
D) 9,12 x10-2
E) 9,12 x 100
Marcos Elantiguo

Solución
Rpta: B
EJERCICIOS DE REFORZAMIENTO PARA LA CASA.
1. Indique la rama de la química que estudia:
I. Obtención del cloruro de sodio. ( ) Qca Analítica
II. Composición química de la fórmula del agua. ( ) Qca Orgánica
III.Extracción del aceite de la aceituna. ( ) Bioquímica
IV. El proceso de respiración de las plantas. ( ) Qca Inorgánica
A) I, II, III, IV B) II, III, IV, I C) II,III, I, IV
D) I, IV, III, II E) IV, III, II, I
Solución
I. Obtención del cloruro de sodio. (II) Qca. Analítica
II. Composición química de la fórmula del agua. (III ) Qca. Orgánica
III.Extracción del aceite de la aceituna. ( IV) Bioquímica
IV. El proceso de respiración de las plantas. (I ) Qca. Inorgánica
Rpta: B
2. La unidad SI de la fuerza es el Newton. Su equivalencia en unidades básicas SI es:
A) kg m s–1
B) kg m s–2
C) g m s–2
D) kg m s2
E) g cm s–2
Solución
Rpta: B
2. Los radios atómicos de los átomos de azufre, arsénico y bromo respectivamente
son: 1,27
o
A , 0,139 nm y 114 pm. Indique el orden decreciente de estos elementos
según sus radios.
Dato: 1
o
A = 10 – 10
m
A) azufre, arsénico, bromo B) arsénico, azufre, bromo
C) arsénico, bromo, azufre D) azufre, bromo, arsénico
E) bromo, azufre, arsénico
Marcos Elantiguo

Solución
Luego: radio arsénico > radio de azufre > radio de bromo
Rpta: B
3. Un mol de átomos de Cesio ocupa un volumen de 7,0 x 101
cm3
. Exprese dicho
volumen en unidades del SI.
A) 7,0 x 10 5
B) 7,0 x 10 – 5
C) 7,0 x 10 6
D) 7,0 x 10 – 6
E) 7,0 x 10 0
Solución
Rpta: B
4. ¿A qué temperatura son iguales las escalas K y R? Exprese el resultado en notación
científica
A) - 7,5 x10–1
B) + 7,5 x101
C) + 7,5 x10–1
D) - 7,5 x101
E) - 7,5 x100
Solución
Rpta: A
5. Una muestra de osmio que pesa 1,123 kg se introduce en un recipiente graduado
que contiene 255 mL de agua elevando el volumen hasta una lectura final de
305 mL. Calcule la densidad del osmio, en g/cm3
, y exprésela en notación científica.
A) 2,246 x 100
B) 2,246 x 101
C) 2,246 x 10-1
D) 2,246 x 102
E) 2,246 x 10-2
Marcos Elantiguo

Solución
Rpta: B
EJERCICIOS PARA SER DESARROLLADOS EN CLASE
GRUPO EJERCICIOS DE CLASE Nº EJERCICIOS DE
REFORZAMIENTO Nº
ADE ( 2 HORAS) 1 al 10 --------
BCF (1 HORA) 2, 3, 4, 6, 8
Biología
EJERCICIOS DE CLASE Nº 01
1. Los dominios de la Biología que permiten estudiar los ecosistemas del planeta y los
cambios de los seres vivos a través del tiempo son la _____________
respectivamente.
A) ecología y la evolución B) ecología y la paleontología
C) bioquímica y la paleontología D) biogeografía y la evolución
E) paleontología y la genética
Solución:
El dominio de la Biología que permite estudiar los ecosistemas del planeta es la
Ecología y la Evolución permite conocer los cambios que han experimentado los
seres vivos a través del tiempo.
Clave: A
2. La descripción de nuevos virus y que afectan la salud del hombre, son materia de
estudio de la
A) bacteriología. B) microbiología. C) micología.
D) evolución. E) virología.
Solución:
La Virología es el dominio de la Biología que estudia las entidades genéticas
denominados virus.
Clave: E
Marcos Elantiguo

3. Los conocimientos científicos y empíricos se asemejan en que ambos
A) se obtienen por una metodología de la ciencia.
B) explican las causas de lo conocido.
C) se obtienen mediante la experiencia.
D) son objetivos y explican la causa de lo conocido.
E) se comprueban a través de la hipótesis.
Solución:
El conocimiento empírico se obtiene mediante la experiencia, no explica las causas
de lo conocido y es subjetivo, mientras que el conocimiento científico se obtiene
mediante un método propio de la ciencia, se comprueba mediante experimentos
rigurosos, explica las causas de lo conocido y es objetivo.
Clave: C
4. El método científico consta de los siguientes pasos generales
A) Observación – hipótesis – experimentación – resultados – conclusiones.
B) Hipótesis – resultados – experimentación – conclusiones – teorías – leyes.
C) Observación – experimentación – resultados – teorías – conclusiones.
D) Hipótesis – experimentación – conclusiones – resultados – leyes.
E) Hipótesis – experimentación – resultados – conclusiones – principios.
Solución:
El método científico a pesar de que los procedimientos puedan variar consta de los
siguientes pasos generales: hacer observaciones, formular hipótesis, someter a
prueba las hipótesis (experimentación y resultados) y llegar a conclusiones.
Clave: A
5. Característica de los seres vivos responsable del crecimiento, mantenimiento y
reparación del organismo.
A) Coordinación B) Metabolismo C) Reproducción
D) Irritabilidad E) Adaptación
Solución:
Los procesos metabólicos que comprenden la degradación de los alimentos, la
obtención de energía y el uso de la materia para producir una nueva son los
responsables del crecimiento, mantenimiento y reparación del organismo.
Clave: B
6. Una laguna es un ejemplo del nivel de organización que corresponde a
A) la ecósfera. B) la comunidad. C) la población.
D) el ecosistema. E) la biosfera.
Solución:
Un ecosistema es el conjunto de comunidades que viven interrelacionándose entre sí
y con las condiciones físico-químicas del lugar en que viven. Un ejemplo de este tipo
de organización es una laguna, acuario.
Clave: D
Marcos Elantiguo

7. La respuesta al “mal de altura” que ocurre cuando se viaja a la sierra es un ejemplo de
A) adaptación. B) coordinación. C) emigración.
D) reparación. E) organización.
Solución:
La respuesta al “mal de altura” se produce por un proceso de adaptación para
superar los factores adversos que hay en su ambiente en un tiempo determinado y
que le permite subsistir.
Clave: A
8. En su organización, los protozoos y las bacterias no tienen los siguientes niveles
a) tisular b) sistémico c) atómico
d) individual e) organológico
A) a,c,e B) a,b,c C) b,c,d D) c,d,e E) a,b,e
Solución:
Los organismos unicelulares no poseen los niveles de organización: tisular,
sistémico, ni organológico.
Clave: E
9. De las siguientes alternativas, ¿cuáles corresponden a complejos supramoleculares?
a) ribosomas
b) proteínas
c) cromosomas
d) nucléolo
e) mitocondria
A) b,c,d B) a,c,d C) c,d,e D) a,d,e E) b,d,e
Solución:
Los complejos supramoleculares surgen como resultado de la interacción de
diferentes macromoléculas, como los ribosomas, cromosomas y nucléolo.
Clave: B
10. Sobre los bioelementos, correlacione ambas columnas y marque la respuesta
correcta.
1. I ( ) coagulación sanguínea
2. Ca ( ) conducción nerviosa
3. Mg ( ) síntesis de tiroxina
4. K ( ) clorofila
A) 2,4,1,3 B) 2,4,3,1 C) 4,3,2,1 D) 3,4,2,1 E) 1, 3,4,2
Solución:
1. I ( 2 ) coagulación sanguínea
2. Ca ( 4 ) conducción nerviosa
3. Mg ( 1 ) síntesis de tiroxina
4. K ( 3 ) clorofila
Clave: A
Marcos Elantiguo

11. Principio inmediato inorgánico que a nivel de las membranas favorece el intercambio
gaseoso y tiene función mecánica amortiguadora.
A) CO2 B) O2 C) Ca CO3 D) NH3 E) H2O
Solución:
El agua es el principio inorgánico que tiene como funciones ser solvente universal,
medio de transporte de sustancias, regulador térmico, mantiene húmedas las
membranas para favorecer el intercambio gaseoso, desempeña una función
mecánica amortiguadora y permite la realización de los procesos de excreción.
Clave: E
12. Sobre los principios orgánicos, correlacione ambas columnas y marque la respuesta
correcta.
1. Proteínas ( ) ácidos grasos- enlaces tipo éster
2. Glúcidos ( ) nucleótidos – enlaces fosfodiester
3. Lípidos ( ) aminoácidos – enlace peptídico
4. Ácidos nucleicos ( ) monosacáridos – enlace glucosídico
A) 3,4,1,2 B) 1,2,3,4 C) 4,3,2,1 D) 2,3,4,1 E) 4,1,2,3
Solución:
1. Proteínas ( 3 ) ácidos grasos- enlaces tipo éster
2. Glúcidos ( 4 ) nucleótidos – enlaces fosfodiester
3. Lípidos ( 1 ) aminoácidos – enlace peptídico
4. Ácidos nucleicos ( 2 ) monosacáridos – enlace glucosídico
Clave: A
13. Son lípidos que en los animales aparecen como sebos y en los vegetales como
aceites.
A) Fosfolípidos B) Glicerol C) Triglicéridos
D) Colesterol E) Ceras
Solución:
Los triglicéridos son los lípidos más abundantes, constituyen sustancias de reserva
que en los animales aparecen como sebos (sólidos) y en los vegetales como líquidos
(aceites).
Clave: C
14. De las siguientes funciones que puede cumplir las proteínas, una es incorrecta.
A) Son catalíticas.
B) Conducen el calor.
C) Regulan el metabolismo.
D) Participan en la defensa del organismo.
E) Transportan moléculas.
Marcos Elantiguo

Solución:
Las proteínas son las moléculas de mayor diversidad funcional: regulan el
metabolismo, proporcionan soporte, transportan moléculas, almacenan nutrientes,
participan en la defensa de un organismo y catalizan las reacciones bioquímicas.
Clave: B
15. En la molécula de ADN, la complementación de bases nitrogenadas se debe a la
formación de enlaces
A) glucosídicos. B) éster. C) fosfodiester.
D) de hidrógeno. E) peptídicos.
Solución:
En la molécula de ADN, la complementación de bases nitrogenadas se debe a la
formación de puentes de hidrógeno.
Clave: D
Marcos Elantiguo

Semana01 ord-2013-i

Más contenido relacionado

La actualidad más candente

Destacado

Similar a Semana01 ord-2013-i

Más de PacoTom14

Último

Semana01 ord-2013-i