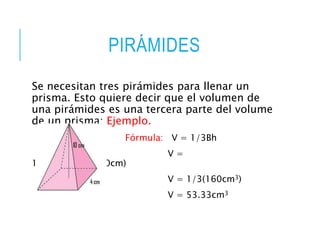
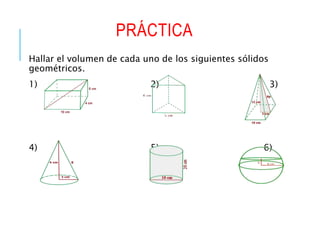
Este documento presenta información sobre sólidos geométricos tridimensionales. Define poliedros, prismas, pirámides y cuerpos redondos como esferas y conos. Incluye fórmulas para calcular el volumen de prismas, pirámides, cilindros, conos y esferas. Finalmente, pide calcular el volumen de varios sólidos geométricos como práctica.

1. ESCUELA DE LA
COMUNIDAD INTERMEDIA
RAFAEL M. DE LABRA.
Materia: Matemáticas
Grado: Octavo
Prof. Francis Martínez Abreu

2. TEMA: SÓLIDOS
GEOMÉTRICOS

3. ESTÁNDAR DE
CONTENIDO
El estudiante es capaz de identificar
formas y dimensiones geométricas, y
utilizar el conocimiento espacial para
analizar su estructura, característica,
propiedades y relaciones para
entender y descubrir el entorno físico .

4. EXPECTATIVA
Aplica los conceptos de
perímetro, área de
superficie y volume para
medir figuras

5. INDICADOR:7.M.12.1
INVESTIGA, ESTABLECE SUPOSICIONES Y APLICA LAS
FÓRMULAS PARA DETERMINAR EL PERÍMETRO, EL ÁREA
DE FIGURAS BIDIMENSIONALES BÁSICAS
(RECTÁNGULOS, PARALELOGRAMOS, TRAPECIOS,
TRAPEZOIDES Y TRIÁNGULOS), EL ÁREA DE
SUPERFICIE Y EL VOLUMEN DE FIGURAS
TRIDIMENSIONALES (PRISMAS, PIRÁMIDES Y
CILINDROS).
.

6. DEFINICIONES
Poliedros: Sólidos geométricos compuestos por caras,
aristas y vértices.
Las caras: son las partes planas del poliedro.
Las aristas: son las líneas que unen las caras.
Los vértices: es la unión de dos aristas.
vértice
cara
arista

7. DEFINICIONES
Los poliedros se clasifican en
prismas y pirámides.
Los prismas son solidos con bases
paralelas congruentes. Entre ellos
se encuentran, los triangulares,
rectangulares, pentagonales,
hexagonales y otros. Ejemplos.

8. DEFINICIONES
Las pirámides son poliedros con una
sola base, algunas de ellas son las
triangulares, rectangulares,
pentagonales y otras. Ejemplos:

9. CUERPOS REDONDOS
Entre los solidos geométricos se
encuentran aquellos de formas
redondas, estos cuerpos tienen toda su
superficie o parte de ella redonda, como
el cilindro, el cono y la esfera. Estos
cuerpos por su forma no son poliedros.
Ejemplos:

10. PRÁCTICA
Dar un nombre a cada sólido geométrico; si en un poliedro
decir, cuantas caras, aristas y vértices tiene.
1) 2) 3)
Nombres:
Caras:
Aristas:
Vértices:
1) Prisma
triangular
5
9
6
7
12
7
7
15
10
2)
Pirámidez
hexagonal
Prisma
pentagonal

11. CONTINUACIÓN DE LA PRÁCTICA
4) 5) 6)
Nombres:
Caras:
Aristas:
Vértices:
4) Prisma
rectangul
ar
6)
Pirámides
triangular
5) Cono
6
12
8
0
0
0
4
6
4

12. VOLUMEN DE
SÓLIDOS
GEOMÉTRICOS
Escuela de la Comunidad
Intermedia
Rafael M. de Labra.
Grado: Octavo
Profesor: Francis Martínez
Abreu

13. DEFINICIONES Y
FÓRMULAS
El volumen de un sólido geométrico se define
como el número de unidades cúbicas que caben
dentro de el. Ejemplo, si observamos el siguiente
prisma rectangular nos damos cuenta que dentro
de el caben un total de 60 unidades cubicas de un
centímetro que representan su volumen. Una forma
corta de hallar ese total es hallar el área de la base
(B), largo(l) por ancho(a) y multiplicarla por la
altura(h). Fórmula: V = Bh
V = lah
V = (5cm)(4cm)(3cm)
V = (20cm2)(3cm)
V = 60 cm3

14. PRISMA TRIANGULAR
En un prisma triangular el área de la base es
un triángulo y por lo tanto esa área es 1/2bh,
luego multiplicamos esa área por la altura del
poligono.
Ejemplo:
V = area de la base del triángulo(B) x altura(h).
V = Bh
V = [1/2(bh) ] X h
V = [1/2(3cm)(4cm)] x 12cm
V = [1/2(12cm2)] x12cm
V = 6cm2 x 12cm
V = 72cm3

15. CILINDRO
En un cilindro el área de la base es
circular, por lo tanto B =𝜋𝑟2
, luego
multiplicamos por la altura del
cilindro(h).
Ejemplo: Fórmula: V =
Bh
V = 𝜋r2 h
V = (3.14)(5in)2 (7in)
V = (3.14)(25in2)(7in)
V = 549.5in3

16. PIRÁMIDES
Se necesitan tres pirámides para llenar un
prisma. Esto quiere decir que el volumen de
una pirámides es una tercera parte del volume
de un prisma: Ejemplo.
Fórmula: V = 1/3Bh
V =
1/3(4cm)(4cm)(10cm)
V = 1/3(160cm3)
V = 53.33cm3

17. CONO
El volumen de un cono es 1/3 parte del volumen de un
cilindro, es decir se necesitan tres cono para llenar un
cilindro.
Fórmula: V = 1/3𝜋r2h
V =
1/3(3.14)(3cm)2(4cm)
V =
1/3(3.14)(9cm2)(4cm)
V = 1/3(113.04cm3)
V = 37.68cm3

18. ESFERA
El volumen de una esfera se determina utilizando la
siguiente fórmula:
V =
4𝜋𝑟3
3
V =
4(3.14)(5𝑐𝑚)3
3
V =
4(3.14)(125𝑐𝑚3)
3
V =
1,570𝑐𝑚3
3
V = 523.33 cm3

19. PRÁCTICA
Hallar el volumen de cada uno de los siguientes sólidos
geométricos.
1) 2) 3)
4) 5) 6)