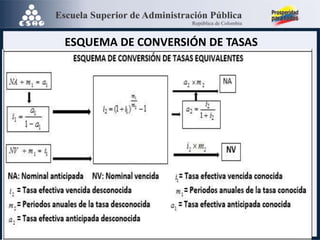
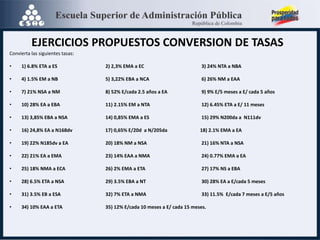
El documento aborda la equivalencia de tasas de interés bajo diferentes modalidades de capitalización y períodos de tiempo, explicando cómo transformar tasas anticipadas y vencidas. Se presentan ejemplos prácticos de cálculos de tasas equivalentes y la importancia de identificar tasas nominales para operaciones financieras. Además, se mencionan conversiones de tasas entre periodos y ejercicios propuestos para consolidar el aprendizaje sobre el tema.

1. EQUIVALENCIA DE TASAS
Bajo la figura de interés compuesto es posible establecer equivalencia de tasas ya sea dentro de un
mismo periodo de tiempo ó con respecto a otro periodo de tiempo, por ejemplo si una obligación
determina una tasa al final del periodo de tiempo, se puede determinar mediante una equivalencia
cual es la tasa que se debe pagar en forma anticipada; también se puede determinar a que tasa
equivale si se considera periodos de tiempo diferentes. Por ejemplo el 2% efectivo mensual que se
debe pagar al final del mes a que tasa es equivalente si se paga al inicio del mes, o que tasa equivale
si se paga cada 3 meses.
Interés periódico ó tasa periódica
Es aquella tasa que efectivamente se reconoce en cada periodo de tiempo y se puede ubicar al inicio
del periodo de tiempo, en cuyo caso se conoce como tasa periódica anticipada (a) o puede estar
ubicada al final del periodo de tiempo , que sería tasa periódica vencida (i) . Esta última es la que
finalmente se contempla en todas las operaciones financieras, por lo que se hace necesario en
muchas ocasiones hacer equivalencias. El siguiente esquema refleja la ubicación en un periodo de
tiempo estas dos tasas.
a
a
i


1 i
i
a


1

2. EQUIVALENCIA DE TASAS EN EL MISMO PERIODO
Ejemplo 1: Se tiene una tasa de interés del 10% efectiva semestral anticipada (ESA), determine su
correspondiente tasa vencida (i) (ES)
En términos porcentuales será 11,11%
Ejemplo 2: Determine la tasa trimestral anticipada (a) (ETA) , equivalente a un 6% efectivo trimestral
vencido ( i ).(ET)
En términos porcentuales será 5,66%
Ejemplo 3: Si debemos pagar el 15% al inicio del año ( 15% EAA) , determine a que tasa vencida es
equivalente ( EA )
En términos porcentuales será 17,65%
1111
,
0
10
,
0
1
10
,
0



i
0566
,
0
06
,
0
1
06
,
0



a
1765
,
0
15
,
0
1
15
,
0



i

3. EQUIVALENCIA DE TASAS - Tasas nominales
Es aquella tasa de interés que se pacta para todo el año, pero que se capitaliza varias veces al
año. Por ejemplo, el 24% nominal trimestral (NT), indica que esta tasa se debe capitalizar
proporcionalmente 4 veces al año, es decir un 6% cada trimestre (ET). Al igual que las tasas
efectivas, la tasa nominal puede pactarse en forma anticipada o vencida.
Con lo expresado anteriormente, estoy indicando que toda tasa nominal se debe dividir entre
el número de periodos que tiene el año para determinar la tasa efectiva periódica. Si la tasa
nominal es vencida, al dividirla entre el número de periodos obtenemos una tasa periodica
vencida (i), pero si la tasa es nominal anticipada, el resultado es una tasa periódica anticipada
(a), lo que obliga a convertirla a efectiva vencida para poder hacer cualquier operación
financiera.
El 16% nominal semestral (NS), indica que la tasa es vencida, al dividirla entre el número de
semestre del año (2), genera una tasa efectiva semestral (i) del 8%. Si la tasa del 16% fuera
nominal semestre anticipado (NSA), indica que hay que dividirla en 2, lo que genera un 8%
efectivo anticipado (a), por lo que hay que pasarla a efectivo vencido (i) para cualquier
operación financiera.
He dicho que toda tasa nominal, ya sea vencida o anticipada, se debe dividir entre los
periodos que tiene un año ( m ) , es decir que si la capitalización es mensual, el número de
periodos (m) es de 12; si es bimestral (m=6); Trimestral (m=4), Semestral (m=2), anual (m=1);
periodos de 7 meses ( m=12/7) , periodos de 2 años (m=12/24 ó ½ ) , periodos de 130 días (
m= 360/130 ) y así sucesivamente.

4. TASAS EQUIVALENTES CON CAMBIO DE PERIODO
Como lo he indicado anteriormente en algunas situaciones se requiere hacer una
conversión de una tasa por su equivalente a otra tasa que debe estar en concordancia
con el nuevo periodo, con el fin de facilitar alguna operación financiera. Por ejemplo,
necesitamos determinar que tasa efectiva anual (EA) es equivalente a una tasa del 10%
efectiva semestral (10% ES). No es como aparentemente se puede pensar que fuera el
20%, no es así porque se trata de un interés compuesto, lo que implica que al final del
primer semestre del año se debe capitalizar un 10% y sobre el interés generado se debe
calcular un nuevo interés. Si un préstamo fuera por $100 al 10% ES (efectivo semestral),
implica que al final del primer semestre el interés es del $10, lo que genera un monto de
$110. Sobre este valor se capitaliza el 10%, es decir $11, lo que genera un monto al final
del año de $121. Este monto con respecto a la inversión de $100, representa un interés
de $21, que con respecto a la inversión equivale al 21%. Entonces concluimos que
podemos reemplazar un 10% ES (efectivo semestral) por su equivalente a un 21% EA
(efectivo anual). Con este análisis, podemos concluir que una tasa de interés es
equivalente a otra cuando se genera el mismo monto al final de un periodo de tiempo.
Para facilitar estas conversiones, podemos hacer uso del siguiente esquema que facilita
su comprensión

5. ESQUEMA DE CONVERSIÓN DE TASAS

6. TASAS COMBINADAS
Son aquellas tasas periódicas compuestas que involucran dos o más tasas, a partir de las cuales se
puede deducir una tasa (i) que las resuma. La ecuación que se deberá plantear es:
Si una operación financiera por ejemplo contempla dos tasas de interés, la tasa (i) que las resume es:
realizando el correspondiente despeje :
Considere que una entidad financiera otorga un préstamo una tasa equivalente al DTF más 12 puntos. El
DTF (Depósito a término fijo), La tasa para depósitos a término fijo (DTF) es un tipo de interés que se
calcula a partir del promedio ponderado semanal por monto de las tasas promedios de captación diarias
de los Certificados de Depósitos a Término a 90 días.
Ó 17,6%
El anterior procedimiento se puede homologar para determinar la rentabilidad total que debe generar un crédito
para cubrir el nivel inflacionario de la economía (F) y una rentabilidad real (R). Con esta precisión la fórmula para
calcular la rentabilidad total sería:
Determine la rentabilidad total que debe generar un proyecto para cubrir un nivel inflacionario (F) del 6% y una
rentabilidad real (R)) del 10%
= = 16,6%
)
1
)......(
1
)(
1
)(
1
(
)
1
( 3
2
1 n
i
i
i
i
i 





1
)
1
)(
1
(
)
( 2
1 


 i
i
i
2
1
2
1 i
i
i
i
i 


12
,
0
*
05
,
0
12
,
0
05
,
0 


i 176
,
0

i
FR
R
F
i 

 R
R
i
F



1 F
F
i
R



1
10
,
0
*
06
,
0
10
,
0
06
,
0 


i 166
,
0

i

7. EJERCICIOS PROPUESTOS CONVERSION DE TASAS
Convierta las siguientes tasas:
• 1) 6.8% ETA a ES 2) 2,3% EMA a EC 3) 24% NTA a NBA
• 4) 1.5% EM a NB 5) 3,22% EBA a NCA 6) 26% NM a EAA
• 7) 21% NSA a NM 8) 52% E/cada 2.5 años a EA 9) 9% E/5 meses a E/ cada 5 años
• 10) 28% EA a EBA 11) 2.15% EM a NTA 12) 6.45% ETA a E/ 11 meses
• 13) 3,85% EBA a NSA 14) 0,85% EMA a ES 15) 29% N200da a N111dv
• 16) 24,8% EA a N168dv 17) 0,65% E/20d a N/205da 18) 2.1% EMA a EA
• 19) 22% N185dv a EA 20) 18% NM a NSA 21) 16% NTA a NSA
• 22) 21% EA a EMA 23) 14% EAA a NMA 24) 0.77% EMA a EA
• 25) 18% NMA a ECA 26) 2% EMA a ETA 27) 17% NS a EBA
• 28) 6.5% ETA a NSA 29) 3.5% EBA a NT 30) 28% EA a E/cada 5 meses
• 31) 3.5% EB a ESA 32) 7% ETA a NMA 33) 11.5% E/cada 7 meses a E/5 años
• 34) 10% EAA a ETA 35) 12% E/cada 10 meses a E/ cada 15 meses.