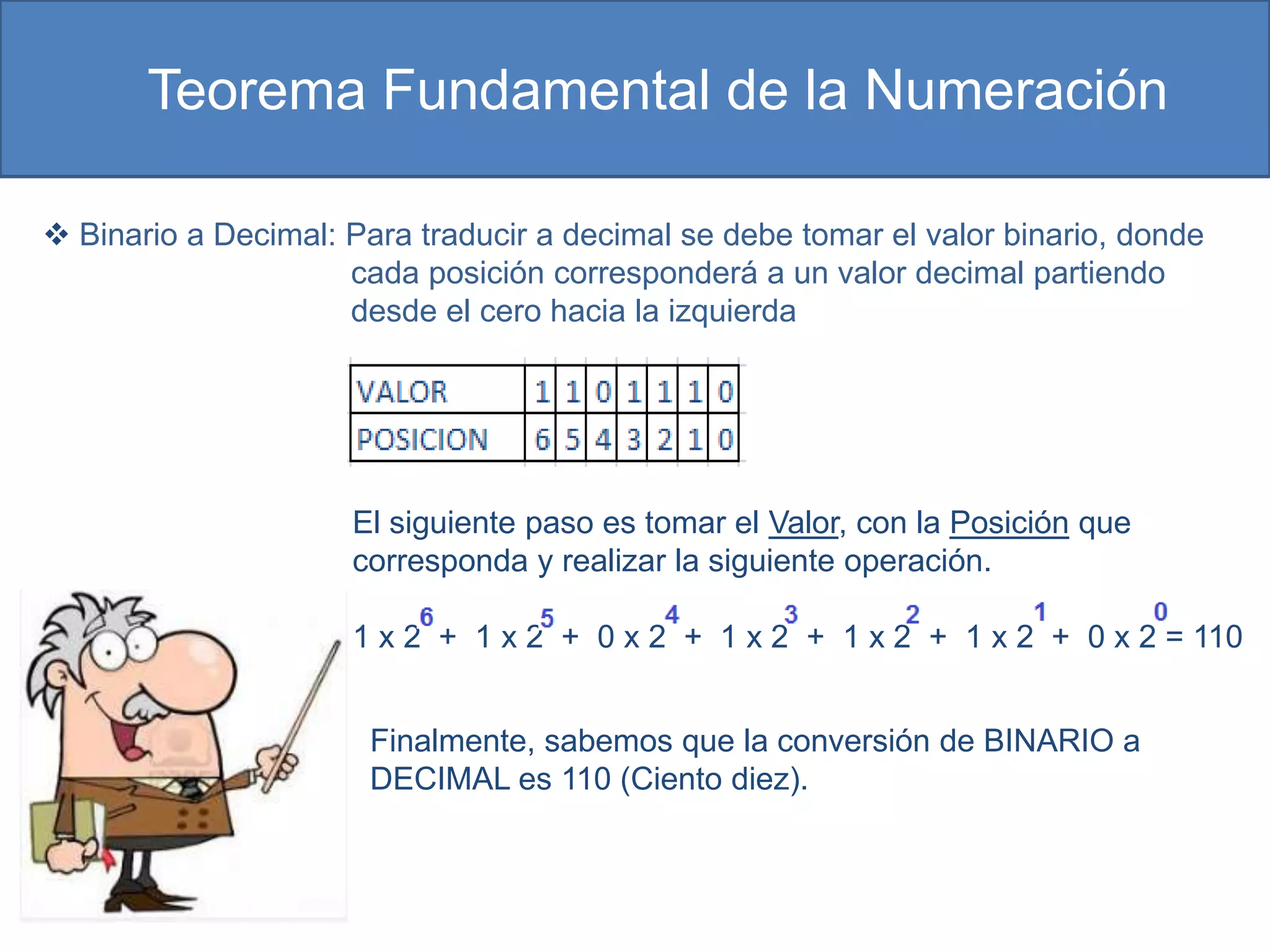
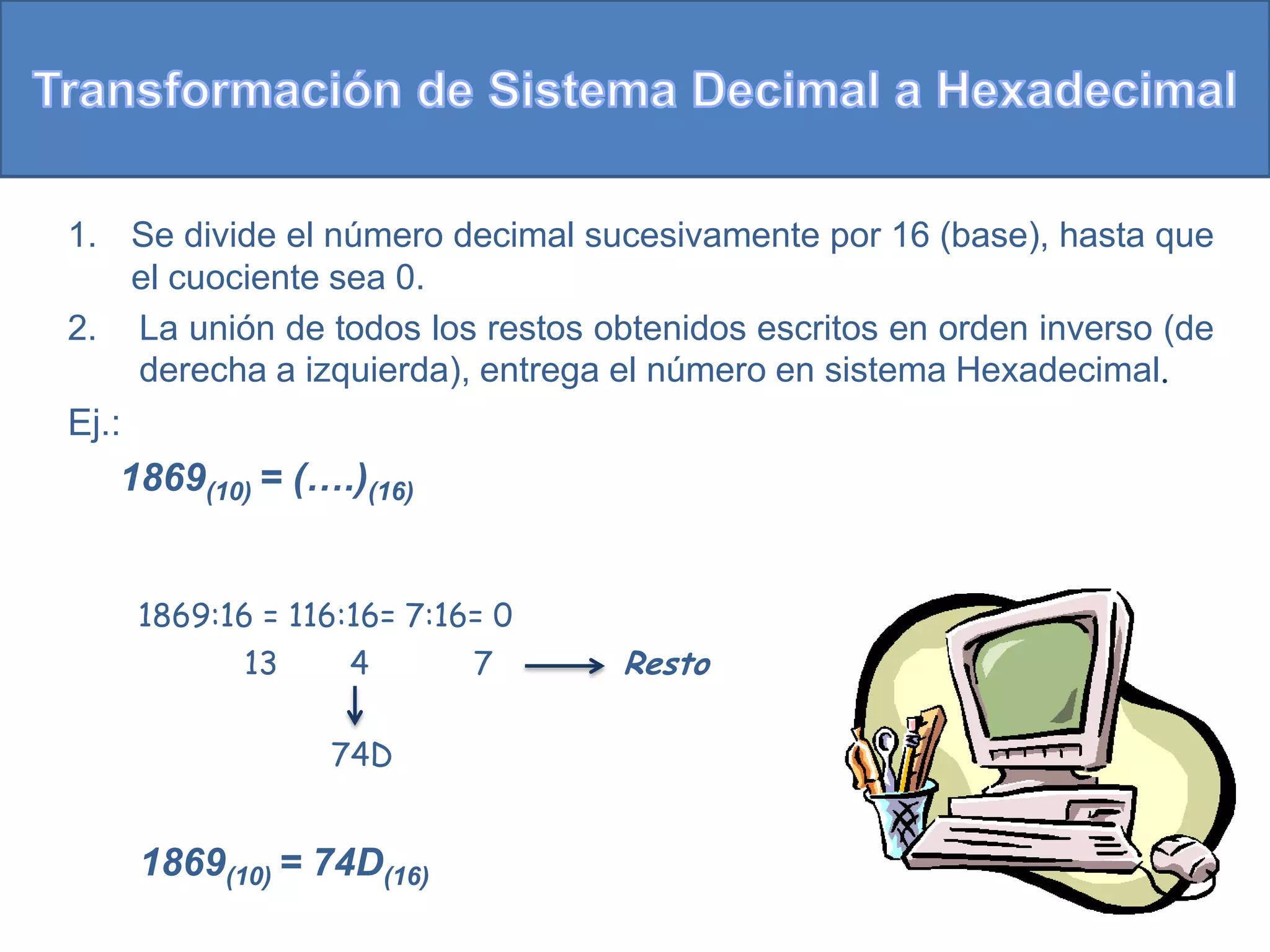
Este documento describe diferentes sistemas numéricos, incluyendo binario, octal, decimal y hexadecimal. Explica las bases y símbolos de cada sistema, y cómo convertir entre sistemas usando el Teorema Fundamental de la Numeración. También cubre cómo los computadores usan el sistema binario para almacenar y transmitir datos.

1. Ingeniería Civil Industrial
Sistemas Numéricos
Alumnos: Romina Moncada Correa
Tomás Pizarro Miqueles

2. Definición
Un sistema numérico es un conjunto de símbolos y reglas de
generación que permiten construir todos los números válidos.
Cada sistema numérico se diferencia de otro por su base.

3. Tipos de Sistemas Numéricos
 Sistema Binario
• Base: 2
• Símbolos: 0,1
 Sistema Octal
• Base: 8
• Símbolos: 0,1,2,3,4,5,6,7
 Sistema Decimal
• Base: 10
• Símbolos: 0,1,2,3,4,5,6,7,8,9
 Sistema Hexadecimal
• Base: 16
• Símbolos: 0,1,2,3,4,5,6,7,8,9,A ,B,C,D,E,F

4. Computadores
La comunicación de los datos
al interior de un computador se
realiza a través de código
binario es decir unos y ceros
(10010010).

5. Código Binario
 BIT
Es la unidad más pequeña de almacenamiento
la cual puede contener el valor 0 o 1
 BYTE
Es una unidad que puede almacenar ocho
bit, es decir un carácter.

6. Otro Sistema Numérico
Otro sistema numérico que tenemos disponible es el Decimal.
Para lo cual existen operaciones que nos permiten traspasar
de un sistema a otro o viceversa.
 Decimal a Binario: La operación que se realiza son divisiones sucesivas
entre dos.
Ejemplo:
15 : 2 = 7; 7 : 2 = 3; 3 : 2 = 1; 1 : 2 = 0
Finalmente, los restos se ordenan de derecha a
izquierda.
15 = 1111

7. Teorema Fundamental de la Numeración
• Este teorema transforma una cantidad expresada en
cualquier sistema de numeración al sistema decimal.
• Su fórmula es:
... + X*B4 + X*B3 + X*B2 + X*B1 + X*B0…
Donde:
X= dígito
B= base del sistema numérico
Exponente= número de posición del dígito

8. Teorema Fundamental de la Numeración
 Binario a Decimal: Para traducir a decimal se debe tomar el valor binario, donde
cada posición corresponderá a un valor decimal partiendo
desde el cero hacia la izquierda
El siguiente paso es tomar el Valor, con la Posición que
corresponda y realizar la siguiente operación.
1 x 2 + 1 x 2 + 0 x 2 + 1 x 2 + 1 x 2 + 1 x 2 + 0 x 2 = 110
Finalmente, sabemos que la conversión de BINARIO a
DECIMAL es 110 (Ciento diez).

9. Teorema Fundamental de la Numeración
 Octal a decimal: Para transformar a decimal se debe tomar el valor
binario, donde cada posición corresponderá a un valor
decimal partiendo desde el cero hacia la izquierda.
Ej.:
2321 (8)= (….)(10)
3210 Posición
• El siguiente paso es tomar el Valor y multiplicarlo con la base elevada a la
posición que corresponda.
2321 = 2*83 + 3*82 + 2*81 + 1*80
2*512 + 3*64 + 2*8 + 1*1
1024 + 192 + 16 + 1
1233
• Finalmente se obtiene que:
2321 (8) = 1233(10)

10. Teorema Fundamental de la Numeración
 Hexadecimal a decimal: Para transformar a decimal se debe tomar el valor
binario, donde cada posición corresponderá a un valor
decimal partiendo desde el cero hacia la izquierda.
Ej.:
4C2E(16) = (….)(10)
4 12 2 14
3 2 1 0 Posición
• El siguiente paso es tomar el Valor y multiplicarlo con la base elevada a la
posición que corresponda.
412214 = 4*163 + 12*162 + 2*161 + 14*160
4*4096 + 12*256 + 2*16 + 14*1
16384 + 3072 + 32 + 14
19502
• Finalmente se obtiene que:
4C2E(16) = 19502(10)

11. 1. Se divide el número decimal sucesivamente por 16 (base), hasta que
el cuociente sea 0.
2. La unión de todos los restos obtenidos escritos en orden inverso (de
derecha a izquierda), entrega el número en sistema Hexadecimal.
Ej.:
1869(10) = (….)(16)
1869:16 = 116:16= 7:16= 0
13 4 7 Resto
74D
1869(10) = 74D(16)

12. Transformación de Sistema Hexadecimal a Binario
• Se convierte el número hexadecimal en decimal, y se aplica método
para la conversión de decimal a binario (se divide sucesivamente por 2
cada digito hasta que el cuociente sea 0).
• Este sistema se representa con 4 dígitos (si lo requiere se agregan
ceros a la izquierda).
Ej.:
8F6(16) = (….)(2)
8 15 6
8:2= 4:2= 2:2= 1:2= 0 15:2= 7:2= 3:2= 1:2= 0 6:2= 3:2= 1:2= 0
0 0 0 1 1 1 1 1 0 1 1
1000 1111 0110
8F6(16) = 100011110110(2)

13. 1. Se separa el número binario en 4 dígitos las veces que sea necesario,
desde la derecha a la izquierda, agregando 0 a la izquierda en los
casos que sea necesario.
2. Luego aplica la conversión de binario a decimal.
3. Finalmente se transforma a Hexadecimal.
Ej.: 1011101(2) = (….)(16)
0101 1101
3 2 1 0 3 2 1 0 Posición
0101 = 23*0 + 22*1 + 21*0 + 20*1 1101 = 23*1 + 22*1 + 21*0 + 20*1
0 + 4 + 0 + 1 8 + 4 + 0 + 1
5 13 D
1011101(2) = 5D(16)

14. Suma de dos números con base 2
• Para sumar dos números binarios, se debe seguir el siguiente
esquema:
0+0=0
0+1=1
1+1=10
1+0 =1
• Esta forma de sumar es semejante a la forma de sumar con base de
10.
• Cuando en una columna el resultado es más de 1 dígito (0 o 1), el
siguiente dígito (1), se suma en la columna que sigue a la izquierda.
Ej.:
1110(2) + 101(2) = 10011(2)
1
1110
+ 101
10 0 1 1

15. GRACIAS POR SU ATENCION