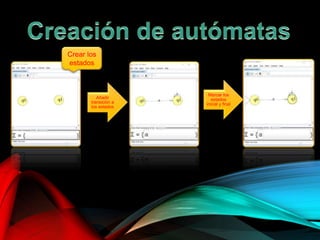
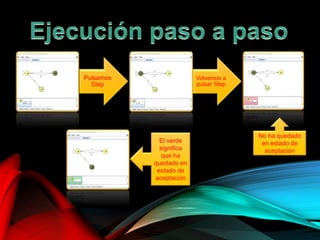
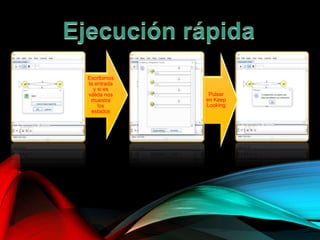
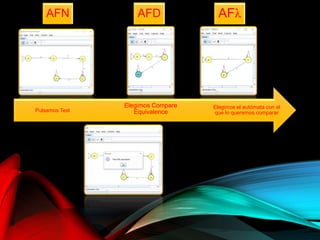
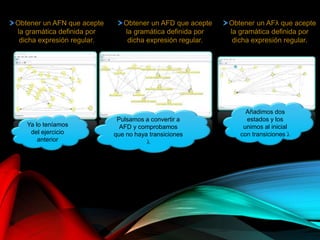
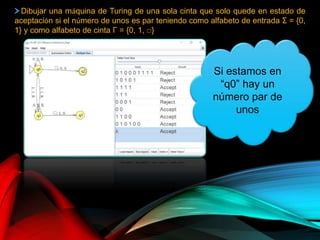
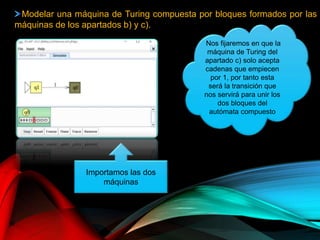
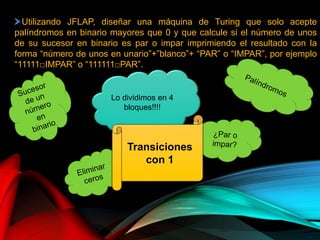
El documento describe la herramienta visual JFLAP, utilizada para construir, probar y depurar autómatas, gramáticas, y lenguajes formales desde su creación en 1990. Explica diversas funcionalidades como la simulación de autómatas, conversión de expresiones regulares, y diseño de máquinas de Turing, destacando ejemplos prácticos y operaciones específicas. La herramienta ha sido adoptada en 161 países para la educación en lenguajes formales y teoría de autómatas.

2. Java Formal Languages and Automata Package
Herramienta visual e interactiva
Construir, probar y depurar:
AFDs y AFNs
Expresiones regulares
Lenguajes
Máquinas de Turing
Gramáticas
Y mucho más!!!

4. Comenzó en 1990 como varias herramientas
Susan H. Rodger
ꜛ NPDA
LR Parser 
LL Analizator
Tubb

5. En 1996 FLAP fue rescrito en Java en la Universidad de Duke
En 2002 fue rescrita de nuevo utilizando Swing
Se utiliza en 161 países diferentes

6. Añadir
transición a
los estados
Marcar los
estados
inicial y final
Crear los
estados

7. Ejecución paso a paso
Ejecución paso a paso con cierre
Ejecución rápida
Ejecución múltiple
Ejecución múltiple como transductor

8. Pulsamos
Step
Volvemos a
pulsar Step
No ha quedado
en estado de
aceptación
El verde
significa
que ha
quedado en
estado de
aceptación

9. Escribimos
la entrada
y si es
válida nos
muestra
los
estados
Pulsar
en Keep
Looking

10. Seleccionamos,
pulsamos en Run inputs
y después en View
Trace

11. Simulación por fuerza bruta
y ver el árbol creado
Saber su tipoIntroducir
una gramática

12. Convertir a AFN

13. AFλAFDAFN
Elegimos el autómata con el
que lo queremos comparar
Elegimos Compare
EquivalencePulsamos Test

14. Utilizando JFLAP, dada la siguiente expresión regular:
(a+b+c)*baba(a+b+c)*
Decir a qué lenguaje pertenece
Convertimos la
expresión a un
AFN y hacemos
una ejecución
múltiple
Comprobamos
que corresponde
a todas las
cadenas que
contiene “baba”

15. Obtener un AFN que acepte
la gramática definida por
dicha expresión regular.
Obtener un AFλ que acepte
la gramática definida por
dicha expresión regular.
Obtener un AFD que acepte
la gramática definida por
dicha expresión regular.
Ya lo teníamos
del ejercicio
anterior
Pulsamos a convertir a
AFD y comprobamos
que no haya transiciones
λ
Añadimos dos
estados y los
unimos al inicial
con transiciones λ

16. Decidir si los autómatas
anteriores son
equivalentes
Decidir si es equivalente a la siguiente gramática
Los comparamos
dos a dos
J  baba J  a
K  λ J  b
J  c K  J
Convertir
a un FA
Lo comparamos
con uno de los
que ya habíamos
creado

17. Dibujar una máquina de Turing de una sola cinta que solo quede en estado de
aceptación si el número de unos es par teniendo como alfabeto de entrada Σ = {0,
1} y como alfabeto de cinta Γ = {0, 1, □}
Si estamos en
“q0” hay un
número par de
unos

18. Dibujar una máquina de Turing de una sola cinta cuyo alfabeto de entrada sea
Σ = {0, 1}, cuyo alfabeto de cinta sea Γ = {0, 1, □} y que solo acepte cadenas de
unos seguidos de ceros, excluyendo la cadena vacía.
q0
acepta
unos
q1
acepta
ceros
q2 es necesario porque
sino la máquina cuando
leyera un cero quedaría
en estado de aceptación
y se pararía

19. Modelar una máquina de Turing compuesta por bloques formados por las
máquinas de los apartados b) y c).
Nos fijaremos en que la
máquina de Turing del
apartado c) solo acepta
cadenas que empiecen
por 1, por tanto esta
será la transición que
nos servirá para unir los
dos bloques del
autómata compuesto
Importamos las dos
máquinas

20. Utilizando JFLAP, diseñar una máquina de Turing que solo acepte
palíndromos en binario mayores que 0 y que calcule si el número de unos
de su sucesor en binario es par o impar imprimiendo el resultado con la
forma “número de unos en unario”+”blanco”+ “PAR” o “IMPAR”, por ejemplo
“11111□IMPAR” o “111111□PAR”.
Lo dividimos en 4
bloques!!!!
Transiciones
con 1

21. Leerá el primer carácter de la
entrada
Recorrerá la cadena hasta el
final
Comprobará si el último es el
mismo carácter que el ya leído
Sustituirá ambos por un blanco
Terminará cuando la cinta solo
tenga blancos
Bloque q0  Palíndromos

22. Si termina en 0  cambio el 0
por 1 y termino
Si termina en 1  cambio todos
los unos por ceros hasta encontrar
un cero, que cambio por un 1 y
termino
Bloque q1  Número siguiente en binario

23. Recorreremos la cadena hasta
llegar a un 0, que cambiamos por X
Seguimos leyendo ceros hasta
encontrar otro 1, que cambiamos por
un 0
Sustituimos la X que por un 1
Cuando no haya más unos en la
cadena a la derecha del control finito,
sustituimos todos los ceros por
blancos
Bloque q2  Eliminación de ceros

24. q0 representa un número par de
unos
q1 representa un número impar de
unos
Cuando se termina la cadena se
imprime el resultado
Bloque q3  ¿Número de unos impar?

25. Lo unimos todo!!!!
Como es un
palíndromo pasa a q1,
de lo contrario se
quedaría en q0
En q1 ya ha calculado
el sucesor, que es el
número que aparece
en la cinta
En q2 ha quitado los
ceros existentes en el
número calculado por
q1, dejando el
resultado en la cinta
en la cinta
En q3 ha comprabado si
el número de unos es
par y ha impreso el
resultado, dejando la
cinta en la forma pedida
en el enunciado

26. Utilizando JFLAP, diseñar una máquina de Turing compuesta por un
bloque, que con varias cintas compruebe si la cadena de entrada es del tipo
AnBnCn tal que n>0, y por otro que la duplique. El resultado final debe tener
la forma AnBnCnAnBnCn, o dicho de otra manera (AnBnCn)2
Entrada y C’s
Copiar B’s
Copiar A’s

27. Marcar el final de la cinta con Y
Marcar el carácter leído con X
Copiarlo en el primer espacio en
blanco
Cuando nos volvamos a encontrar
la Y, copiar el primer carácter en su
lugar

28. Unimos la máquina AnBnCn con la que copia
Pasa de q0 a q1
porque el
número de As,
Bs y Cs es igual
Una vez que ha
terminado la
ejecución de q2,
la cadena de
entrada queda
duplicada en la
cinta