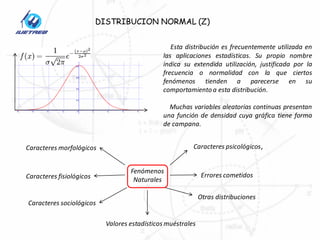
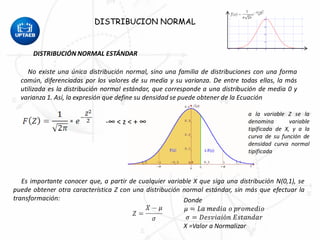
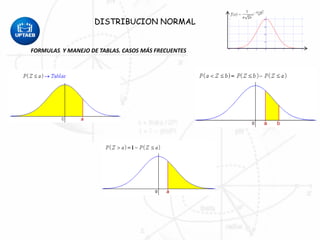
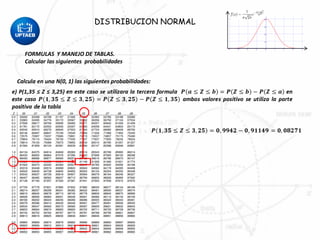
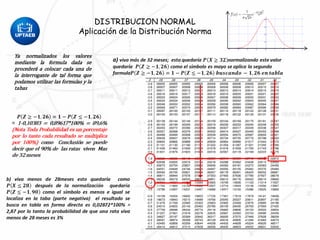
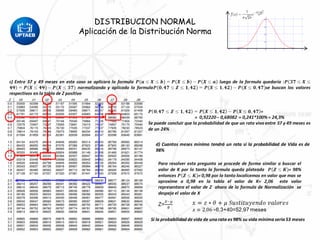
Este documento describe la distribución normal y sus propiedades. Explica que muchas variables aleatorias continuas siguen esta distribución y presentan una curva en forma de campana. La distribución normal tiene una única moda, media y mediana. También describe cómo calcular probabilidades usando tablas de la distribución normal estándar y cómo aplicar la distribución normal para resolver problemas estadísticos.

1. DISTRIBUCION NORMAL (Z)
Esta distribución es frecuentemente utilizada en
las aplicaciones estadísticas. Su propio nombre
indica su extendida utilización, justificada por la
frecuencia o normalidad con la que ciertos
fenómenos tienden a parecerse en su
comportamientoa esta distribución.
Muchas variables aleatorias continuas presentan
una función de densidad cuya gráfica tiene forma
de campana.
Fenómenos
Naturales
Caracteres morfológicos
Caracteres fisiológicos
Caracteres sociológicos
Caracteres psicológicos,
Errores cometidos
Valores estadísticos muéstrales
Otras distribuciones

2. DISTRIBUCION NORMAL
Tiene una única moda, que coincide con su media y su mediana.
La curva normal es asintótica al eje de abscisas. Por ello, cualquier valor entre
-∞ y +∞ y es teóricamenteposible. El área total bajo la curva es, por tanto, igual a 1.
Es simétrica con respecto a su media μ . Según esto, para este tipo de variables existe
una probabilidad de un 0.50 de observar un dato mayor que la media μ y un 0.50 de
observar un dato menor.
La distancia entre la línea trazada en la media y el punto de inflexión de la curva es igual
a una desviación típica σ Cuanto mayor sea , más aplanada será la curva de la densidad.
El área bajo la curva comprendido entre los valores situados aproximadamente a dos
desviaciones estándar de la media es igual a 0.95. En concreto, existe un 0.95 de
posibilidades de observar un valor comprendido en el intervalo . (μ - 1.96 σ μ+ 1.96 σ)
Propiedades de la distribución normal:
La distribución normal posee ciertas propiedades importantes que conviene destacar:

3. DISTRIBUCION NORMAL
DISTRIBUCIÓN NORMAL ESTÁNDAR
No existe una única distribución normal, sino una familia de distribuciones con una forma
común, diferenciadas por los valores de su media y su varianza. De entre todas ellas, la más
utilizada es la distribución normal estándar, que corresponde a una distribución de media 0 y
varianza 1. Así, la expresión que define su densidad se puede obtener de la Ecuación
a la variable Z se la
denomina variable
tipificada de X, y a la
curva de su función de
densidad curva normal
tipificada
-∞ < z < + ∞
Es importante conocer que, a partir de cualquier variable X que siga una distribución N(0,1), se
puede obtener otra característica Z con una distribución normal estándar, sin más que efectuar la
transformación:

4. CARACTERÍSTICA DE LA DISTRIBUCIÓN NORMAL ESTÁNDAR (REDUCIDA, TIPIFICADA )
No depende de ningún parámetro
Su media es 0, su varianza es 1 y su desviación típica es 1.
La curva f(x) es simétrica respecto del eje OY
Tiene un máximo en este eje
Tiene dos puntos de inflexión en z =1 y z = -1
Esta propiedad resulta especialmente interesante en la práctica, ya que para una distribución
existen tablas y formulas publicadas a partir de las que se puede obtener de modo sencillo la
probabilidad de observar un dato menor o igual a un cierto valor z, y que permitirán resolver
preguntas de probabilidad acerca del comportamiento de variables de las que se sabe o se asume que
siguen una distribución aproximadamente normal.
DISTRIBUCION NORMAL

5. DISTRIBUCION NORMAL
FORMULAS Y MANEJO DE TABLAS. CASOS MÁS FRECUENTES

6. DISTRIBUCION NORMAL
FORMULAS Y MANEJO DE TABLAS.
Calcular las siguientes probabilidades
Calcula en una N(0, 1) las siguientes probabilidades:
a) P(Z ≤ 2,35)
b) P(Z ≤ -1,86)
c) P(Z ≥ 1,77)
d) P(1,35 ≤ Z ≤ 3,25)
e)P(Z≤ k)=0.7611
Solución: a) P(Z ≤ 0,35) ya que este es un valor esta a la izquierda ( que
menor e igual ) el valor de probabilidad pedido se busca
directamente en la tabla de la siguiente forma: la tabla
consta de dos parte los Z positivos (+) y los Z negativos (-)
como el valor es positivo se utilizara la parte positiva de la
tabla, el valor buscado es 0,35 ( Valor Positivo ) el primer
numero entero y el primer decimal se busca en la parte
izquierda de la tabla positiva columna de Z seria entonces
0,3 y en la parte superior se localiza el ultimo decimal en
este caso 0,05 para completar el valor buscado 0,35 se
intersecta los dos valores y se consigue la probabilidad
pedida que es 0,63683 Nota( Todos los valores de la tabla
vienen precedidos de cero (0) ) entonces P(Z ≤ 0,35) =0,63683

7. DISTRIBUCION NORMAL
FORMULAS Y MANEJO DE TABLAS.
Calcular las siguientes probabilidades
Calcula en una N(0, 1) las siguientes probabilidades:
b) P(Z ≤ -1,86) valor negativo se utiliza la parte negativa de la tabla y como es un valor menor que
Se busca directamente en tabla entonces el valor de la probabilidad 0,03144
Solución

8. DISTRIBUCION NORMAL
FORMULAS Y MANEJO DE TABLAS.
Calcular las siguientes probabilidades
Calcula en una N(0, 1) las siguientes probabilidades:

9. DISTRIBUCION NORMAL
FORMULAS Y MANEJO DE TABLAS.
Calcular las siguientes probabilidades
Calcula en una N(0, 1) las siguientes probabilidades:

10. e)P(Z≤ k)=0.7611 en este caso donde se pide busca el valor de
k tendremos que proceder de esta forma:
Como el símbolo es menor e igual se busca el valor
directamente en tabla , pero la pregunta ¿ Como entramos a
la tabla? La respuesta es tenemos que encontrar el valor
dado en este caso 0,7611 o el que se aproxima mas a el
dentro de la tabla ¿En cual? Tendremos que buscarlo el valor
que mas se aproxima se muestra en tabla que es 0,76115 y
vamos de adentro de la tabla hacia afuera primero al lado
izquierdo donde esta el valor de Z en este caso es 0,7 y
después a la parte superior 0,01 por lo tanto el valor de K=
0,71 , otro ejemplo si fuera P(Z≤ k)=0.6628 se procede de la
misma forma se busca el valor que se aproxime mas a 0,6628
en esta caso el valor de K= 0,42
DISTRIBUCION NORMAL
FORMULAS Y MANEJO DE TABLAS.
Calcular las siguientes probabilidades
Calcula en una N(0, 1) las siguientes probabilidades:

11. Ejemplos
DISTRIBUCION NORMAL
Aplicación de la Distribución Norma
1-Un investigador de la UCLA reporta que las ratas viven un promedio de 40 meses cuando sus dietas son muy restringidas y
luego enriquecidas con vitaminas y proteínas. Suponiendo que las vidas de tales ratas están normalmente distribuidas con
una desviación estándar de 6.3meses, encuentre la probabilidad de que una rata determinada
a) viva más de 32 meses;
b) menos de 28 meses;
c) entre 37 y 49 meses
d) Cuantos meses mínimo tendrá de
vida un ratón si la probabilidad de
Vida es de 98%
Nota: Para resolver este ejercicio
se tiene primero que normalizar
los valores ya que la media o
promedio y desviación estándar
son diferente de 0 y 1 para esto
usaremos la formula :
Usando las misma formula para
los demás valores se obtienen
Para (28 Z= -1,90); (37 Z=0,47) ; (49 Z= 1,42)

12. DISTRIBUCION NORMAL
Aplicación de la Distribución Norma
Ya normalizados los valores
mediante la formula dada se
procederá a colocar cada una de
la interrogante de tal forma que
podamos utilizar las formulas y la
tabas

13. DISTRIBUCION NORMAL
Aplicación de la Distribución Norma
d) Cuantos meses mínimo tendrá un rata si la probabilidad de Vida es de
98%
Si la probabilidad de vida de una rata es 98% su vida mínima seria 53 meses