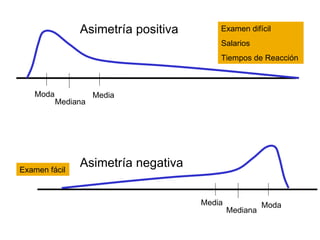
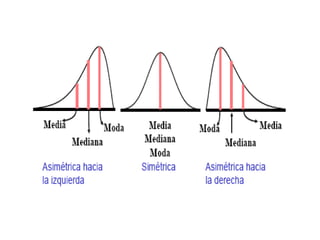
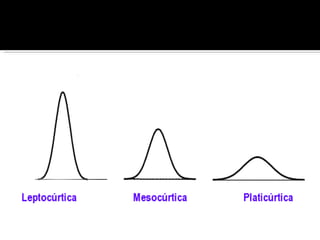
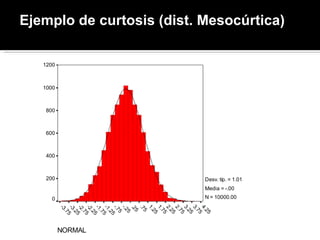
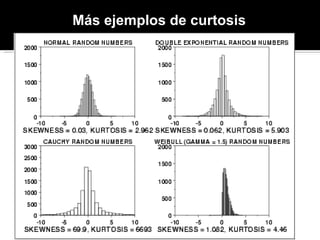
Este documento explica los conceptos de asimetría y curtosis para describir las características de una distribución de datos. Define la asimetría positiva y negativa y dos índices para medirla. También define la curtosis leptocúrtica y platicúrtica en comparación con una distribución normal, e introduce un índice para medir el grado de curtosis.

1. Asimetría y curtosis En los dos temas anteriores hemos visto las medidas de tendencia central y las medidas de variabilidad. Si bien la obtención de tales medidas es clave para describir una muestra y efectuar inferencias sobre la población de origen, es también fundamental saber obtener una caracterización adecuada de los datos.

2. Asimetría Si bien es fácil tener una idea de si la distribución es simétrica o no tras ver la representación gráfica (p.e., un histograma o un diagrama de caja y bigotes), es importante cuantificar la posible asimetría de una distribución. Recordemos que cuando la distribución de los datos es simétrica, la media, la mediana y la moda coinciden. (Y la distribución tiene la misma forma a la izquierda y la derecha del centro) Si bien muchas distribuciones psicológicas se asume que tienden a ser simétricas y unimodales, en muchos casos la distribución que encontramos es asimétrica (v.g., las distribuciones de los Tiempos de Reacción en casi cualquier tarea es asimétrica positivo).

3. Asimetría positiva Moda Mediana Media Asimetría negativa Media Mediana Moda Examen difícil Salarios Tiempos de Reacción Examen fácil

5. Índices de asimetría 1. Índice de asimetría de Pearson Muy sencillo de calcular. Está basado en la relación entre la media y la moda en distribuciones simétricas y asimétricas: Si la distribución es simétrica A s será 0 Si la distribución es asimétrica positiva, A s será mayor que 0 Si la distribución es asimétrica negativa, A s será menor que 0

6. Índices de asimetría 2. Índice de asimetría de Fisher Está basado en la diferencia de los datos sobre la media, como la varianza, si bien esta vez se elevan los coeficientes al cubo Si la distribución es simétrica A s será 0 Si la distribución es asimétrica positiva, A s será mayor que 0 Si la distribución es asimétrica negativa, A s será menor que 0 Desventaja: Muy influida por puntuaciones atípicas (ya lo volveremos a comentar en el último punto de este tema).

7. Curtosis o apuntamiento Hace referencia al apuntamiento de la distribución en relación a un estándar, que es la distribución normal. Este estándar es la distribución normal: distribución mesocúrtica. Si la distribución es más apuntada que la distribución normal tenemos una distribución leptocúrtica. Si la distribución es más achatada que la distribución normal tenemos una distribución platicúrtica.

9. Curtosis o apuntamiento IMPORTANTE: Curtosis es independiente de la variabilidad (en el sentido de “varianza”). Es decir, no es que una distribución leptocúrtica tenga menos varianza y por eso es más apuntada. Una distribución leptocúrtica es muy apuntada en el centro (más que la normal), decae muy rápidamente en un primer momento, pero en los extremos es algo más alta que la distribución normal. Eso quiere decir que una distribución leptocúrtica es más probable que ofrezca más valores extremos que la distribución normal.

10. Ejemplo de curtosis (dist. Mesocúrtica)

11. Índice de curtosis (veremos un solo índice) Para una distribución normal (mesocúrtica) sabemos que Y esta va a ser la referencia para el índice de curtosis que vamos a emplear Si la distribución es normal (mesocúrtica), el índice vale 0 Si la distribución es leptocúrtica, el índice es superior a 0 Si la distribución es platicúrtica, el índice es inferior a 0

12. Más ejemplos de curtosis