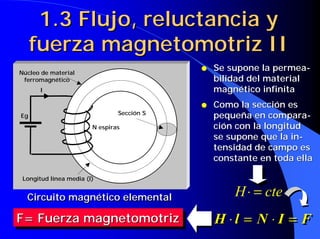
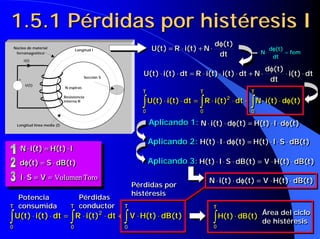
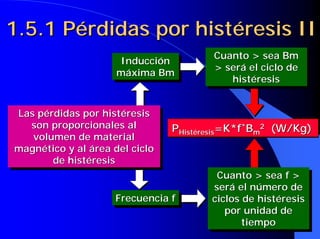
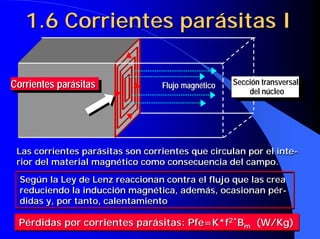
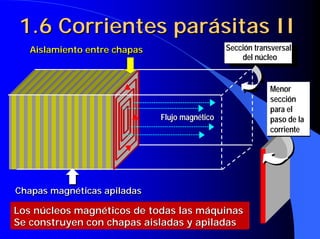
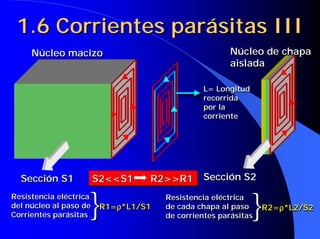
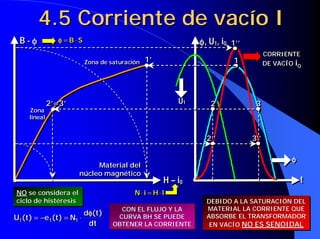
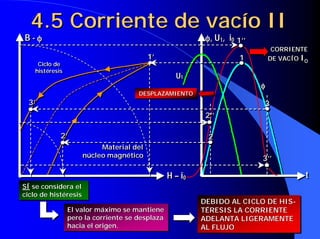
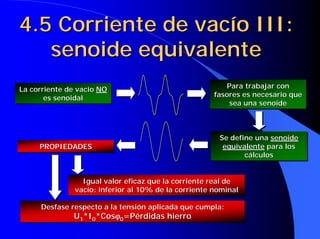
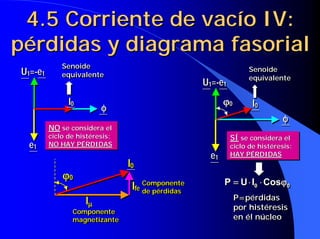
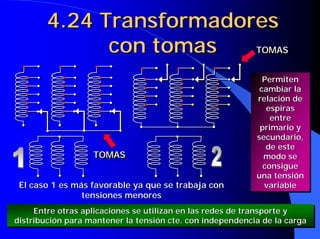
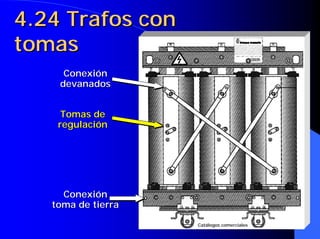
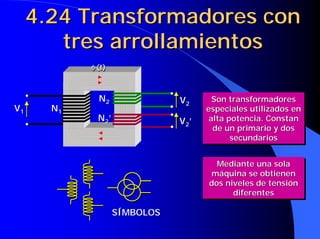
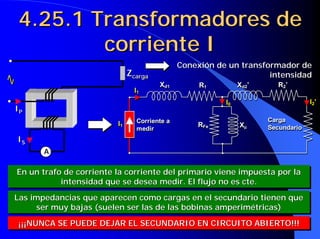
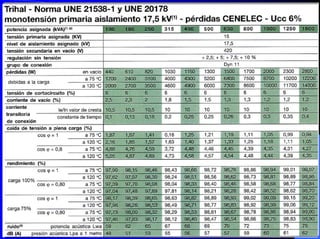
Este documento resume las leyes fundamentales del electromagnetismo. Explica el teorema de Ampere, la inducción magnética, el flujo magnético, la reluctancia, la fuerza magnetomotriz y la ley de Faraday. También define las unidades de las magnitudes electromagnéticas como el tesla, weber y amperio-vuelta. Por último, describe el ciclo de histéresis magnética de los materiales ferromagnéticos.









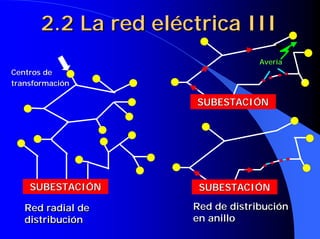








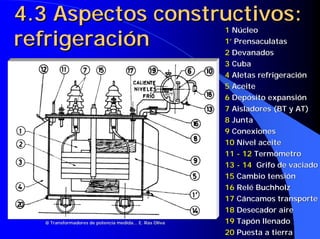



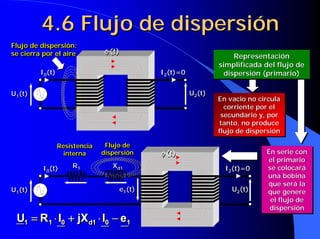
![4.10 Diagrama fasorial del
transformador en carga
jXd1*I1
R1*I1 e 2 = I 2 ⋅⋅ [R 2 + jX d2 ] + U2
2 = 2 2 + d2 + 2
U2 estará
U2 estará
adelantada
adelantada
U1 U2 = Z c ⋅⋅ I 2
2 = c 2 un ángulo ϕ2
un ángulo ϕ2
respecto a I2
respecto a I2
Suponiendo carga inductiva:
Suponiendo carga inductiva:
-e1
-e
Zc=Zc ϕ2 → I2 estará retrasada
Zc=Zc ϕ2 → I2 estará retrasada Las caídas de
Las caídas de
ϕ1 I1
I2’ respecto de e2 un ángulo ϕ:
respecto de e2 un ángulo ϕ: tensión en R1
tensión en R1
y Xd1 están
y Xd1 están
I0 Z c ⋅⋅ Senϕ2 + X d2
ϕ 2 + d2
ϕ = atg c
ϕ= R + Z ⋅ Cosϕ aumentadas.
aumentadas.
ϕ
ϕ 2 + c ⋅
2 c ϕ2
2 En la práctica
En la práctica
I2 son casi
son casi
ϕ2
I1 = I 0 + I 2 ' = I 0 − 2
1 = 0 + 2 = 0 − despreciables
despreciables
ϕ rtt
e2
e2
Las caídas de
U1 − I1 ⋅⋅ [R 1 + jX d1 ] + e1 = 0
U2 Las caídas de
1 − 1 1 + d1 + 1 = tensión en R2
tensión en R2
I2
y Xd2 también
U1 = − e1 + I1 ⋅⋅ [R 1 + jX d1 ]
y Xd2 también
e1
e1 1 = − 1+ 1 1+ d1 son casi nulas
son casi nulas](https://image.slidesharecdn.com/primer20parcial20completo-121118052226-phpapp01/85/Primer-20parcial-20completo-64-320.jpg)

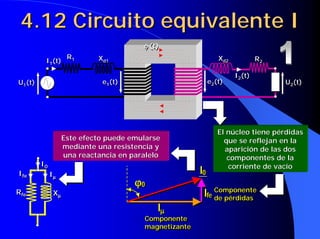
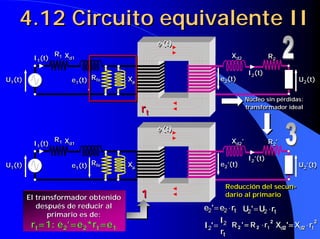
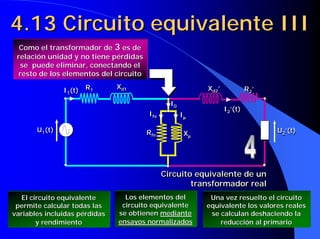

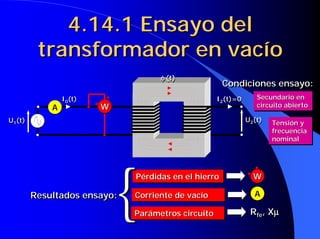
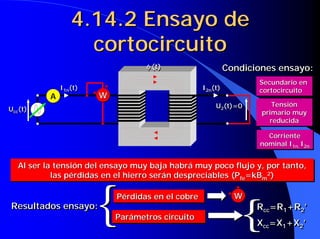
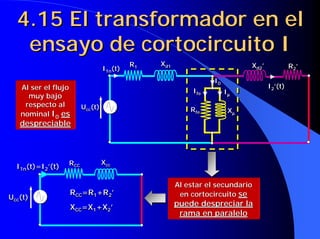
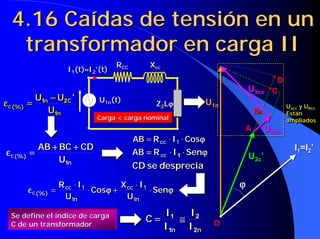
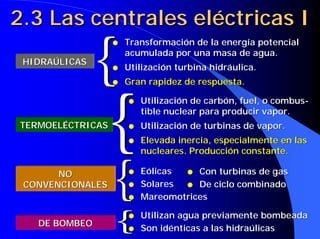
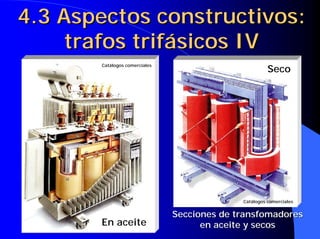
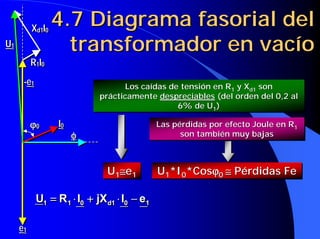
![4.16 Caídas de tensión en un
transformador en carga III
R ⋅⋅ I
R I X ⋅⋅ I
X I I1n
I1n
ε c (%) = cc 1 ⋅⋅ Cosϕ + cc 1 ⋅⋅ Senϕ
ε c (%) = cc 1 Cosϕ + cc 1 Senϕ Multiplicando por:
Multiplicando por:
U1n
U1n U1n
U1n I1n
I1n
R cc ⋅ I1 I1n X cc ⋅ I1 I1n
ε c (%) =
ε c (%) cc 1 ⋅ 1n ⋅ Cosϕ +
ϕ cc 1 ⋅ 1n ⋅ Senϕ
ϕ
U1n
1n I1n
1n U1n
1n I1n
1n
ε RCC
RCC C
C
ε c (%) = C ⋅ [ε RCC ⋅ Cosϕ + ε XCC ⋅ Senϕ]
ε c (%) εRCC ϕ ε XCC ϕ EFECTO
EFECTO
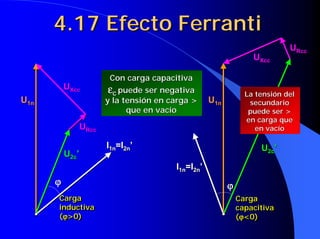
FERRANTI
FERRANTI
Si ϕ < 0 ⇒ Senϕ < 0 ⇒ ε c puede ser < 0 ⇒ U2 c ' > U1n ⇒ U2 c > U2n
ϕ< ⇒ ϕ < ⇒ εc < ⇒ 2 c > 1n ⇒ 2 c > 2n](https://image.slidesharecdn.com/primer20parcial20completo-121118052226-phpapp01/85/Primer-20parcial-20completo-76-320.jpg)
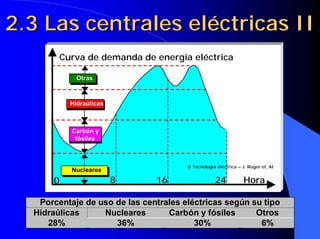
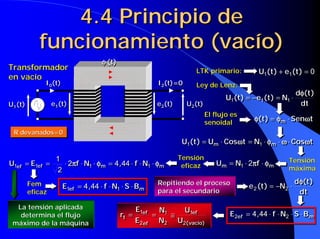
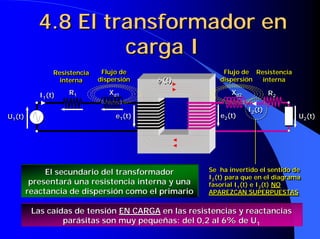
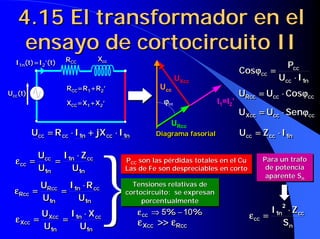
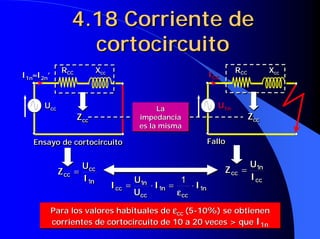
![4.18 Rendimiento del
transformador
Pcedida P P2
η=
η = cedida = 2= 2 P1 = P2 + Pfe + Pcu η=
η=
1 = 2 + fe + cu
2
Pabsorbida P1
absorbida 1 P2 + Pfe + Pcu
2 + fe + cu
Pcu = R 1 ⋅⋅ I1 2 + R 2 '⋅⋅I 2 '2 ≅ R cc ⋅⋅ I1 2 = R cc ⋅⋅ I1n 2 ⋅⋅ C 2 = Pcc ⋅⋅ C 2
2 2 2
cu = 1 1 + 2 2 2 ≅ cc 1 = cc 1n 2
= cc 2
I1 I2
1 ≅ C=
=
≅ 2 EL TRANSFORMADOR
EL TRANSFORMADOR
I1n I2n
1n 2n TRABAJA CON UN
TRABAJA CON UN
U2I 2Cosϕ
U2I 2Cosϕ C ⋅⋅ U2I 2nCosϕ
C U2I 2nCosϕ ÍNDICE DE CARGA C
ÍNDICE DE CARGA C
η=
η= =
=
U2I 2Cosϕ + P0 + Pcc C 2 C ⋅⋅ U2I 2nCosϕ + P0 + Pcc C 2
U2I 2Cosϕ + P0 + Pcc C 2 C U2I 2nCosϕ + P0 + Pcc C 2
Ensayo de vacío
Ensayo de vacío
U2 n − U2 C
2n − 2 C
ε c (%) =
ε c (%) = U2 c = [1 − ε c ]⋅⋅ U2n
2c = − ε c U2 n
U2 n
2n
C ⋅⋅ [1 − ε c ]⋅⋅ U2nI 2nCosϕ
− εc ϕ C ⋅⋅ [1 − ε c ]⋅⋅S n Cosϕ
− εc n ϕ
η=
η= 2 n 2n =
=
C ⋅⋅ [1 − ε c ]⋅⋅U2nI 2nCosϕ + P0 + Pcc C2 C ⋅⋅ [1 − ε c ]⋅⋅S n Cosϕ + P0 + Pcc C 2
− εc 2 n 2n ϕ + 0 + cc 2 − εc n ϕ + 0 + cc 2](https://image.slidesharecdn.com/primer20parcial20completo-121118052226-phpapp01/85/Primer-20parcial-20completo-78-320.jpg)
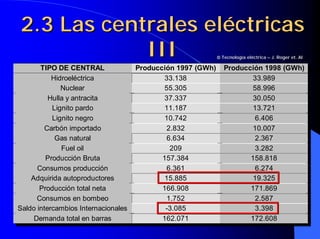
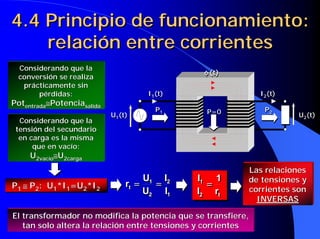
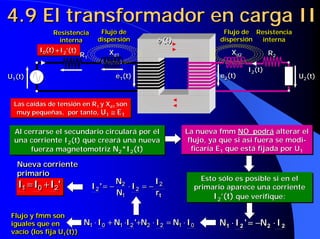
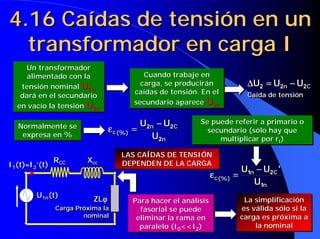
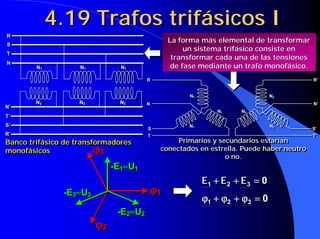
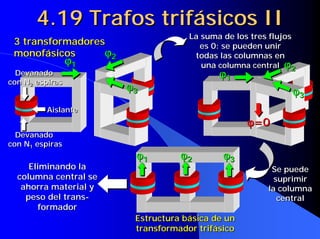
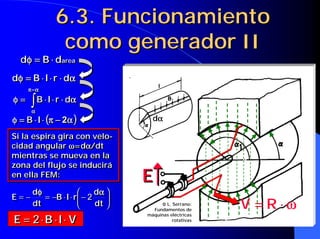
![4.19 Influencia del índice de
carga y del cosϕ en el rendimiento
cosϕ
C ⋅⋅ [1 − ε c ] ⋅⋅S n Cosϕ
− εc n ϕ Despreciando
Despreciando
η=
η= la caída de
C ⋅⋅ [1 − ε c ]⋅⋅S n Cosϕ + P0 + Pcc C 2
− εc n ϕ + 0 + cc 2
la caída de
tensión
tensión
C ⋅⋅S n Cosϕ
ϕ
C ⋅⋅S n C = cte Cosϕ = var iable η=
η= n
η=
η= n
C ⋅⋅S n Cosϕ + P0 + Pcc C 2
ϕ + 0 + cc 2
K n
C ⋅⋅S n +
n+
Cosϕ ϕ
C= variable
C= variable
Cosϕ ↑ ⇒ η ↑
Cosϕ= Cte
Cosϕ= Cte
ϕ
η
P0
0 + P C mín. η =
S n Cosϕ
n ϕ
η max si
η + cc η=
C cc P0
S n Cosϕ + 0 + Pcc C
n ϕ+ + cc
C
ϕ
Cosϕ
ϕ
Derivando
Derivando P0
C ηmax = C
ηmax =
respecto a C e
respecto a C e 0
Pcc Cηmax
ηmax
igualando a 0
igualando a 0 cc](https://image.slidesharecdn.com/primer20parcial20completo-121118052226-phpapp01/85/Primer-20parcial-20completo-79-320.jpg)
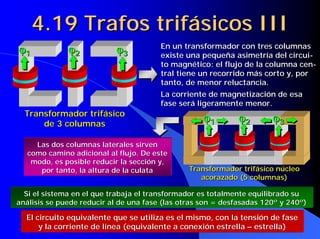







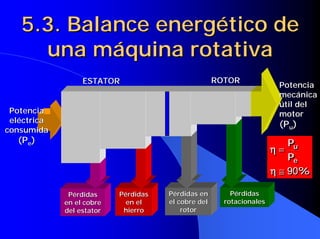



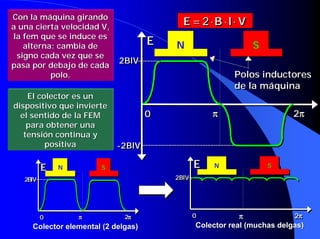


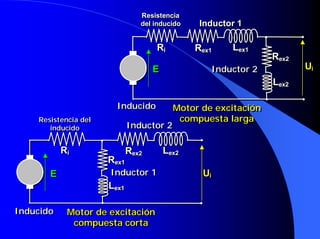
![6.9. La máquina de CC como
I
generador II
En la generador en derivación la propia
Rii
Rex
ex
tensión de salida del generador se
utiliza para producir la excitación
E Uii Uex
ex Uex=Ui
Lex
ex
E Curva de magnetización
Inducido
Inducido Inductor
Inductor
Generador con excitación E2
Pto. de
derivación equilibrio
El generador “arranca” gracias al magnetismo E1
remanente siguiendo un proceso de
AUTOEXCITACIÓN E = I ⋅⋅ [R ex + R ii ]
E = I R ex + R
Magnetismo ϕR ER
ER
remanente ER IR =
IR =
R ex + R ii
R ex + R
Se repite hasta el ER Iex
pto. de equilibrio E2 I1 E1
IR I1](https://image.slidesharecdn.com/primer20parcial20completo-121118052226-phpapp01/85/Primer-20parcial-20completo-122-320.jpg)
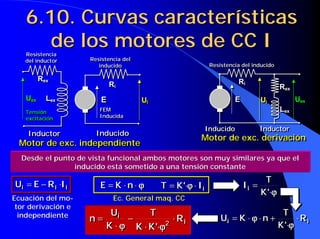
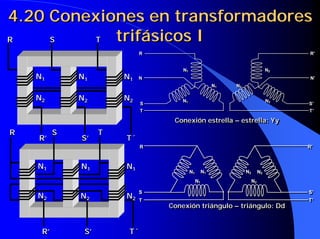
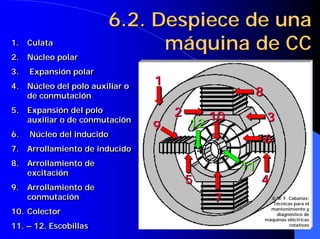
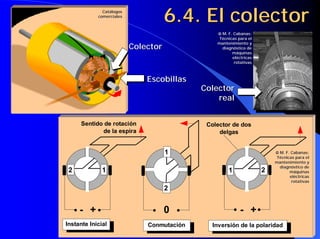
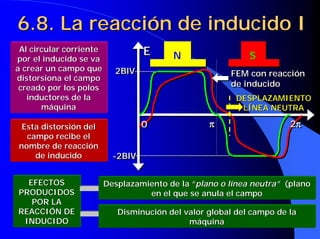
![6.10. Curvas características
de los motores de CC III
Resistencia del
Resistencia del
inducido
inducido Inductor
Inductor En el motor serie el devanado de
Iii=Iex
ex
excitación y el inducido están conectados
Rii Rex
ex Lex
Lex en serie. Iex=Ii y esta última depende de
la carga arrastrada por el motor, por tan-
Uii to, sus características funcionales serán
E
Ii=Iex U
distintas de las del motor de exc. indep.
Inducido
Inducido
E = Uii − [R ii + R ex ] ⋅Iii
ex
Ecuación del
motor serie
Motor de excitación serie
Motor de excitación serie
n=
Uii − [R ii + R ex ] ⋅ Iii
ex n=
Uii [R + R ex ]⋅ T
− ii ex
E = K ⋅n⋅ϕ
ϕ
K ⋅ϕ ϕ K ⋅ϕϕ K ⋅ K '⋅ϕ 2
ϕ2
Ec. General maq. CC
La relación entre ϕ
ϕ
T = K '⋅ϕ ⋅ Iii
ϕ Iex y el flujo ϕ
viene definida por Zona lineal
Zona lineal
Ec. General maq. CC la característica ϕ=CIex
ϕ=CIex
magnética (B-H)
de la máquina Iex
Iex](https://image.slidesharecdn.com/primer20parcial20completo-121118052226-phpapp01/85/Primer-20parcial-20completo-125-320.jpg)
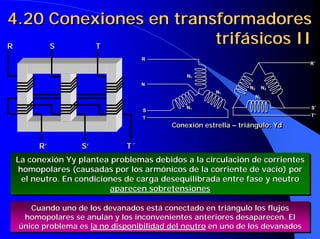
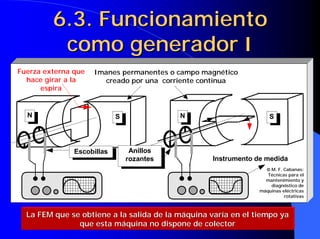
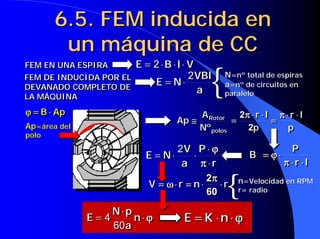
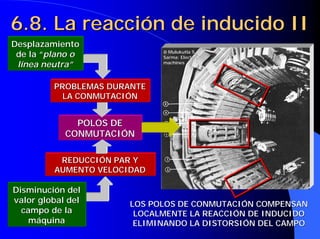
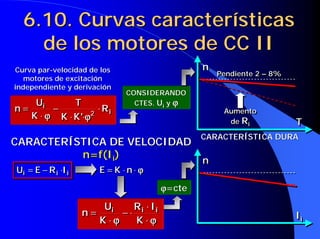
![6.10. Curvas características
de los motores de CC V
CARACTERÍSTICA DE VELOCIDAD n=f(Ii)
E = Uii − [R ii + R ex ] ⋅Iii
ex
Ecuación del
motor serie n
En la zona de
E = K ⋅n⋅ϕ
ϕ Ec. General maq. CC saturación es
una recta
Uii = K ⋅ ϕ ⋅ n + Iii ⋅ [R ii + R ex ]
ϕ ex
decreciente
U I ⋅ [R ii + R ex ] Iii
n= − ii ex Como Iex=Ii en
K ⋅ϕ
ϕ K ⋅ϕ ϕ la zona lineal del
n=
U [R + R ex ]
− ii ex
motor se cumple:
ϕ=CIi
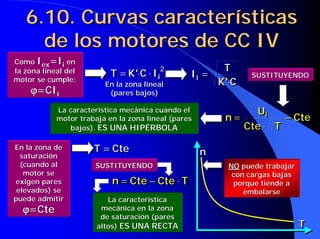
En la zona de saturación se
Cte ⋅ Iii Cte puede admitir ϕ=Cte
La característica de velocidad cuando el motor U I ⋅ [R ii + R ex ]
trabaja en la zona lineal ES UNA HIPÉRBOLA n= − ii ex
Cte Cte](https://image.slidesharecdn.com/primer20parcial20completo-121118052226-phpapp01/85/Primer-20parcial-20completo-127-320.jpg)