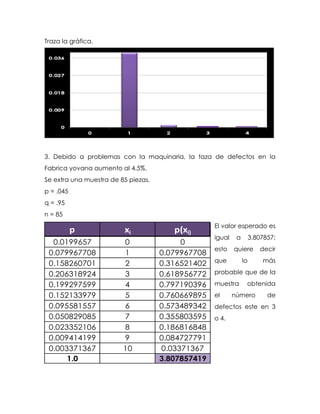
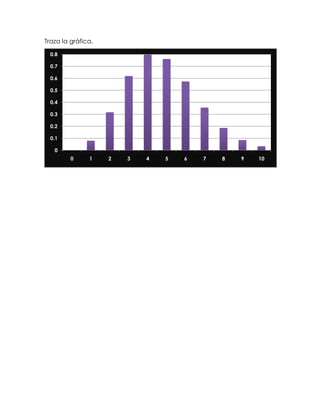
Este documento presenta tres problemas de probabilidad y estadística relacionados con la tasa de defectos en una fábrica de marcadores. El primer problema calcula la probabilidad de 0 a 4 defectos en una muestra de 4 piezas con una tasa de defectos del 1%. El segundo problema calcula la probabilidad de 0 a 10 defectos en una muestra de 85 piezas con una tasa de defectos del 4.5%. El tercer problema grafica la distribución de probabilidad del segundo problema.

1. INGENIERIA EN TECNOLOGIAS DE LA
PRODUCCIÓN
ESTADÍSTICA
PROBABILIDAD
DOCENTE: EDGAR MATA ORTIZ
ALUMNA: DULCE GONZALEZ SALCIDO
TORREÓN COAH.

2. p xi p(xi)
0.960596 0 0
0.038811 1 0.038811
0.000588 2 0.001176
0.00000396 3 0.00001188
0.0000001 4 0.0000004
1.0 0.03999928
2. En la Fábrica de marcadores yovana se sabe que tiene un nivel de
calidad entre 2 y 3 sigma, por lo que la tasa de defectos es del 1%. Se
extrae una muestra de 4 piezas.
Determine la probabilidad de que haya:
a) 0 defectos
b) 1 defecto
c) 2 defectos
d) 3 defectos
e) 4 defectos.
Traza la gráfica y determina el valor esperado.
Cálculos:
n = 4
p = .01
q = .99
El valor esperado es
de 0.03999; esto
quiere decir que de
esta muestra lo más
probable es que no
haya defectos.

3. p xi p(xi)
0.0199657 0 0
0.079967708 1 0.079967708
0.158260701 2 0.316521402
0.206318924 3 0.618956772
0.199297599 4 0.797190396
0.152133979 5 0.760669895
0.095581557 6 0.573489342
0.050829085 7 0.355803595
0.023352106 8 0.186816848
0.009414199 9 0.084727791
0.003371367 10 0.03371367
1.0 3.807857419
Traza la gráfica.
3. Debido a problemas con la maquinaria, la taza de defectos en la
Fabrica yovana aumento al 4.5%.
Se extra una muestra de 85 piezas.
p = .045
q = .95
n = 85
El valor esperado es
igual a 3.807857;
esto quiere decir
que lo más
probable que de la
muestra obtenida
el número de
defectos este en 3
o 4.

4. Traza la gráfica.
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0 1 2 3 4 5 6 7 8 9 10