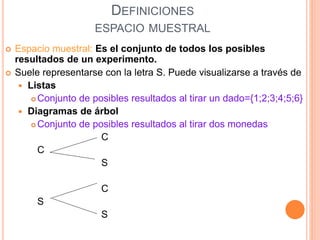
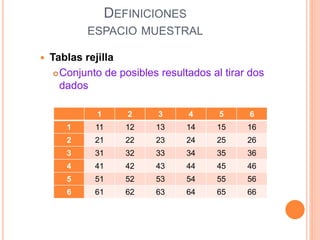
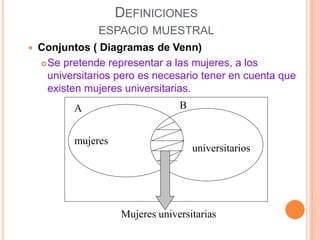
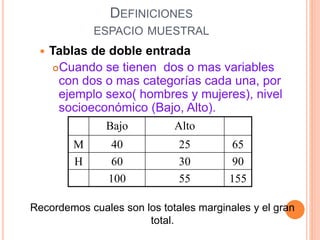
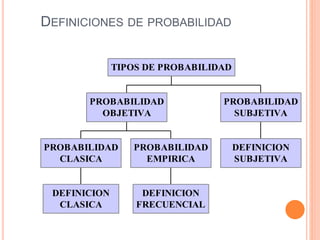
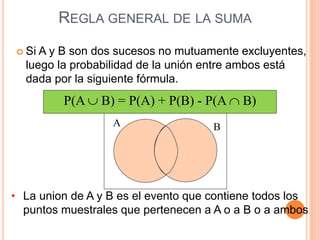
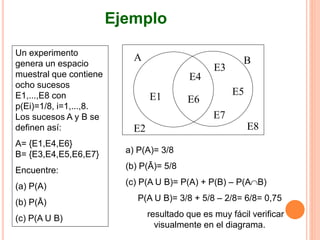
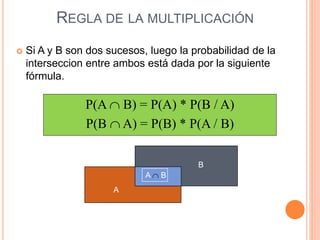
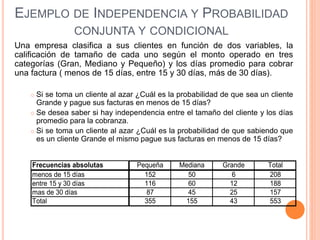
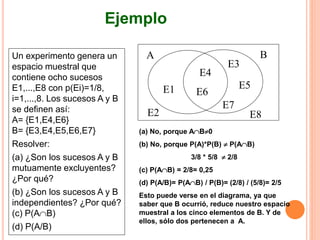
Este documento presenta los conceptos fundamentales de la teoría de probabilidades. Explica definiciones como experimento aleatorio, espacio muestral, evento, probabilidad clásica, frecuencial y subjetiva. También cubre temas como variables aleatorias, distribuciones de probabilidad como binomial, Poisson, normal y Student. Por último, analiza conceptos como probabilidad conjunta, condicional e independencia.

1. Temas a desarrollar
Experimento aleatorio, espacio muestral y resultado.
Eventos (simples y compuestos). Breve teoría de
conjuntos. Definiciones de probabilidad. Propiedades.
Probabilidad condicional. Eventos dependientes e
independientes. Teorema de Bayes.
Variable aleatoria. Caso discreto y continuo. Función
de densidad y de distribución poblacional. Esperanza
y varianza. Propiedades. Distribuciones Binomial,
Poisson, Normal y Student. Distribución normal
estándar. Aplicaciones.

2. La teoría de probabilidades comienza a desarrollarse en el siglo XVII
en Francia con dos notables matemáticos, Blaise Pascal y Pierre de
Fermat, por la correspondencia entre ellos sobre un requerimiento de
un noble Francés y jugador Chevalier de Méré.
Se dice que de Méré había apostado en el lanzamiento de cuatro
dados al menos un 6 aparecerá. El había ganado consistentemente,
pero para atraer a mas gente a jugar, cambió el juego a: en 24
lanzamientos de dos dados, un par de 6 aparecerá.
Según se cuenta de Méré perdía con 24 lanzamientos y creía que 25
lanzamientos necesarios para hacer el juego favorable a él.
Problemas como estos Pascal y Fermat resolvieron e influyeron con
ello a investigadores como Huygens, Bernoulli, and DeMoivre para
establecer la teoría de probabilidades.
Hoy en día la teoría de probabilidades esta muy desarrollada y es la
base de muchas de las aplicaciones utilizadas para la toma de
decisiones
Origen de la Teoría de Probabilidades

3. El uso de la teoría de probabilidades ayuda para comprender la
variabilidad y de esta forma hace que las organizaciones puedan
resolver problemas con mayor eficiencia y eficacia.
La variabilidad puede observarse en el comportamiento y en el
resultado de muchas actividades, incluso bajo aparentes condiciones
de estabilidad.
La variabilidad puede observarse en las características medibles de
muchos procesos.
La teoría de probabilidades es muy útil para resolver problemas de
análisis cuantitativo como ser:
Análisis de decisiones, modelos de regresión, de pronósticos, de
administración de proyectos y de teoría de colas.
Modelación y simulación. Control estadístico de la calidad. Teoría de
juegos. Scoring bancario y de seguros
Uso de la teoría de Probabilidades

4. DEFINICIONES
 Probabilidad: Es un valor comprendido entre 0 y 1, incluidos
estos dos valores, que describe la posibilidad de ocurrencia de un
evento.
 Experimento: Cualquier proceso que produce un resultado.
 Determinístico: Ante la repetición del mismo se obtiene
siempre el mismo resultado.
 Aleatorio: Repitiendo el experimento en idénticas condiciones
se obtienen distintos resultados.
 Punto muestral ó Resultado: Es un resultado particular de un
experimento.
 Evento: Es una colección de uno o mas resultados de un
experimento.
 Espacio muestral: Es el conjunto de todos los resultados
experimentales

5. DEFINICIONES
EVENTO O SUCESO ALEATORIO
 Evento o Suceso Aleatorio: Es una colección de uno o
mas resultados de un experimento.
 E1=Sacar un 5 al tirar un dado
 E2=Sacar un número par al tirar un dado.
 E3=Sacar un número menor que 7 al tirar un
dado=EVENTO CIERTO
 E4=Sacar un número mayor que 6 al tirar un
dado=EVENTO IMPOSIBLE

6. DEFINICIONES
ESPACIO MUESTRAL
 Espacio muestral: Es el conjunto de todos los posibles
resultados de un experimento.
 Suele representarse con la letra S. Puede visualizarse a través de
 Listas
 Conjunto de posibles resultados al tirar un dado={1;2;3;4;5;6}
 Diagramas de árbol
 Conjunto de posibles resultados al tirar dos monedas
C
C
S
C
S
S
4-3

7. DEFINICIONES
ESPACIO MUESTRAL
 Tablas rejilla
Conjunto de posibles resultados al tirar dos
dados
4-3
1 2 3 4 5 6
1 11 12 13 14 15 16
2 21 22 23 24 25 26
3 31 32 33 34 35 36
4 41 42 43 44 45 46
5 51 52 53 54 55 56
6 61 62 63 64 65 66

8. DEFINICIONES
ESPACIO MUESTRAL
 Conjuntos ( Diagramas de Venn)
Se pretende representar a las mujeres, a los
universitarios pero es necesario tener en cuenta que
existen mujeres universitarias.
4-3
A B
mujeres
universitarios
Mujeres universitarias

9. DEFINICIONES
ESPACIO MUESTRAL
 Tablas de doble entrada
Cuando se tienen dos o mas variables
con dos o mas categorías cada una, por
ejemplo sexo( hombres y mujeres), nivel
socioeconómico (Bajo, Alto).
Bajo Alto
M 40 25 65
H 60 30 90
100 55 155
Recordemos cuales son los totales marginales y el gran
total.

10. DEFINICION
CLASICA
PROBABILIDAD
CLASICA
DEFINICION
FRECUENCIAL
PROBABILIDAD
EMPIRICA
PROBABILIDAD
OBJETIVA
DEFINICION
SUBJETIVA
PROBABILIDAD
SUBJETIVA
TIPOS DE PROBABILIDAD
DEFINICIONES DE PROBABILIDAD
4-4

11. DEFINICIÓN CLASICA
 Se basa en que todos los resultados son
 Igualmente probables o equiprobables.
 Mutuamente excluyentes
 Colectivamente exhaustivos
 Es necesario conocer el espacio muestral y los resultados
Número de resultados favorables
Probabilidad de un evento =
Número de resultados posibles
Ejemplo: Sea el experimento de tirar dos monedas a la vez
•El espacio muestral será S = {CC, CS, SC, SS}
•Consideremos el evento de que salga una sola cara.
•Probabilidad de una sola cara = {CS, SC}/{CC, CS, SC, SS}=
= 2/4 = ½ = 0,5.

12. DEFINICIÓN FRECUENCIAL
 Cuando los resultados no son equiprobables la
probabilidad de ocurrencia de un evento se determina por
observación del número de veces que eventos similares
ocurrieron en el pasado. (frecuencia relativa)
Número de veces que el evento ocurrió en el pasado
Probabilidad de un evento =
Número de observaciones
Ejemplo: Sea el experimento de estudiar una droga que
cura cierta enfermedad en vacunos enfermos. Se aplicó
a 1000 vacunos y se curaron 700.
•El espacio muestral será S = {curado; no curado}
•Consideremos el evento de que el vacuno se cure.
•Probabilidad de curado = 700/1000=0,7

13. LEY DE LOS GRANDES NÚMEROS
 La definición frecuencial se apoya en la ley de los
grandes números.
 Si realizamos un experimento de lanzar una moneda un
cierto número de veces y calculamos la frecuencia
relativa de la aparición de cara.
 Podremos observar que la frecuencia relativa del suceso
cara tiende a estabilizarse en 0,5.
 A esto lo llamaremos probabilidad de un suceso.

14. El naturalista francés Buffon lanzó una moneda
4.040 veces. Resultando 2.048 caras, una
razón de 2.048/4.040 = 0,5069
El matemático inglés John Kerrich, mientras fue
prisionero de los alemanes durante la Segunda
Guerra Mundial, lanzó una moneda 10.000 veces.
Resultando 5.067 caras, una razón de 0,5067
Alrededor de 1900, el estadístico inglés Karl
Pearson en un acto sin precedentes lanzó una
moneda 24.000 veces. Resultando 12.012
caras, una razón de 0,5005
Ejemplos de ensayos realizados

15.  Se quiere estudiar la demanda de camisas en una gran tienda
departamental, para ver los talles que se demandan, para ello se
utilizaron los registros de las ventas diarias del último año y se obtuvo
la siguiente tabla
 ¿Cuál es la probabilidad de vender en un año una camisa de talle 42?
 ¿Cuál es la probabilidad de vender en un año una camisa de talle 41?
EJEMPLO
Talle
Número de camisas
vendidas
Frecuencia
Relativa
38 231 0,065
39 343 0,097
40 520 0,147
41 685 0,193
42 897 0,253
43 540 0,152
44 333 0,094
TOTAL 3549 1

16. DEFINICIÓN SUBJETIVA
 Cuando no se tienen datos para ningún tipo de cálculo,
ni posibilidad de efectuar repetidamente el experimento,
se recurre a un experto, quien de acuerdo a su buen
saber y entender estimará la probabilidad.
Ejemplos:
•Calcular la probabilidad de que un tenista gane un
campeonato
•Calcular la probabilidad de que un club de futbol salga
campeón
•Calcular la probabilidad de que el precio de las acciones de
una compañía se incremente en dos años.

17. AXIOMAS DE PROBABILIDADES
 Independientemente de que definición de
probabilidad utilicemos, siempre se deberán
cumplir los siguientes tres axiomas.
Axiomas:
•Axioma 1: La probabilidad de un evento existe y es un
número mayor o igual a cero
)
(
0 A
P

•Axioma 2: La probabilidad de todo el espacio muestral es 1.
P(S)=1
•Axioma 3: Si dos eventos A y B son mutuamente
excluyentes
P(AB)=P(A)+P(B)

18. CONSECUENCIAS DE LOS AXIOMAS DE
PROBABILIDADES
1. P()=0
2. Si Ā = suceso complementario de A es
decir Ā = S – A, será P(Ā) = 1 – P(A)
3. Si A1A2, entonces P(A1)  P(A2)
4.  A se cumple que P(A)  1

19. REGLA GENERAL DE LA SUMA
 Si A y B son dos sucesos no mutuamente excluyentes,
luego la probabilidad de la unión entre ambos está
dada por la siguiente fórmula.
P(A  B) = P(A) + P(B) - P(A  B)
• La union de A y B es el evento que contiene todos los
puntos muestrales que pertenecen a A o a B o a ambos
A B

20. DEFINICIONES
SUCESOS COMPUESTOS
 Sucesos mutuamente excluyentes:
 Dos sucesos A y B son mutuamente excluyentes
cuando la ocurrencia de uno de ellos impide la
ocurrencia del otro. Es decir, el echo que ocurra A
impide que ocurra B
 P(A  B) = P(A y B) = P (AB) = 0
 Sucesos colectivamente exhaustivos
 Dos sucesos A y B son colectivamente exhaustivos
cuando al menos uno de ellos deba ocurrir siempre que
se realiza el experimento.
 Dicho en otras palabras, deberá cumplirse que la suma
de las probabilidades de todos los sucesos deberá ser
igual a 1. La unión de los sucesos posibles da como
resultado el espacio muestral (S).

21. Un experimento
genera un espacio
muestral que contiene
ocho sucesos
E1,...,E8 con
p(Ei)=1/8, i=1,...,8.
Los sucesos A y B se
definen así:
A= {E1,E4,E6}
B= {E3,E4,E5,E6,E7}
Encuentre:
(a) P(A)
(b) P(Ā)
(c) P(A U B)
A B
E1
E4
E6
E7
E3
E5
E8
E2
a) P(A)= 3/8
(b) P(Ā)= 5/8
(c) P(A U B)= P(A) + P(B) – P(AB)
P(A U B)= 3/8 + 5/8 – 2/8= 6/8= 0,75
resultado que es muy fácil verificar
visualmente en el diagrama.
Ejemplo

22. En una agencia bancaria hay dos sistemas de alarma A y
B. El sistema A funciona en 7 de cada 10 atracos, B
funciona en 8 de cada 10 y los dos a la vez lo hacen 6 de
cada 10 atracos.
¿Cuál es la probabilidad de que en caso de atraco
funcione al menos una de estas alarmas?
Solución: Se definen los sucesos
A:”El sistema A funciona”
B:”El sistema B funciona”
9
,
0
6
,
0
8
,
0
7
,
0
)
(
6
,
0
)
(
8
,
0
)
(
7
,
0
)
(








B
U
A
P
B
A
P
B
P
A
P
Ejemplo

23. REGLA DE LA MULTIPLICACIÓN
 Si A y B son dos sucesos, luego la probabilidad de la
interseccion entre ambos está dada por la siguiente
fórmula.
P(A  B) = P(A) * P(B / A)
P(B  A) = P(B) * P(A / B)
A  B
A
B

24. INDEPENDENCIA
 Dos eventos A y B son independientes cuando se
cumple que la probabilidad conjunta es igual al
producto de las probabilidades marginales.
P(A  B) = P(A)*P(B)

25. PROBABILIDAD CONDICIONAL
• Probabilidad Condicional es la probabilidad de
ocurrencia de un evento en particular, dado que el
otro evento ha ocurrido. La probabilidad condicional
del evento A dado que el evento B ha ocurrido se
escribe P(A/B).
P(A / B) = P(A  B)
P(B)
• El suceso A este caso es el suceso incierto sobre el cual desea calcularse
su probabilidad y el suceso B es el suceso cierto, el suceso B representa un
subconjunto del espacio muestral.

26. EJEMPLO DE INDEPENDENCIA Y PROBABILIDAD
CONJUNTA Y CONDICIONAL
Una empresa clasifica a sus clientes en función de dos variables, la
calificación de tamaño de cada uno según el monto operado en tres
categorías (Gran, Mediano y Pequeño) y los días promedio para cobrar
una factura ( menos de 15 días, entre 15 y 30 días, más de 30 días).
 Si se toma un cliente al azar ¿Cuál es la probabilidad de que sea un cliente
Grande y pague sus facturas en menos de 15 días?
 Se desea saber si hay independencia entre el tamaño del cliente y los días
promedio para la cobranza.
 Si se toma un cliente al azar ¿Cuál es la probabilidad de que sabiendo que
es un cliente Grande el mismo pague sus facturas en menos de 15 días?
Frecuencias absolutas Pequeña Mediana Grande Total
menos de 15 días 152 50 6 208
entre 15 y 30 días 116 60 12 188
mas de 30 días 87 45 25 157
Total 355 155 43 553

27. EJEMPLO DE INDEPENDENCIA Y PROBABILIDAD
CONDICIONAL
 Si se toma un cliente al azar ¿Cuál es la probabilidad de que sea un cliente
Grande y pague sus facturas en menos de 15 días?
 Se desea saber si hay independencia entre el tamaño del cliente y los días
promedio para la cobranza.
 Si se toma un cliente al azar ¿Cuál es la probabilidad de que sabiendo que es
un cliente Grande el mismo pague sus facturas en menos de 15 días?
Probabilidad Conjunta Pequeña Mediana Grande Total
menos de 15 días 0,275 0,090 0,011 0,376
entre 15 y 30 días 0,210 0,108 0,022 0,340
mas de 30 días 0,157 0,081 0,045 0,284
Total 0,642 0,280 0,078 1,000
Producto de las marginales Pequeña Mediana Grande Total
menos de 15 días 0,241 0,105 0,029 0,376
entre 15 y 30 días 0,218 0,095 0,026 0,340
mas de 30 días 0,182 0,080 0,022 0,284
Total 0,642 0,280 0,078 1,000

28. Un experimento genera un
espacio muestral que
contiene ocho sucesos
E1,...,E8 con p(Ei)=1/8,
i=1,...,8. Los sucesos A y B
se definen así:
A= {E1,E4,E6}
B= {E3,E4,E5,E6,E7}
Resolver:
(a) ¿Son los sucesos A y B
mutuamente excluyentes?
¿Por qué?
(b) ¿Son los sucesos A y B
independientes? ¿Por qué?
(c) P(AB)
(d) P(A/B)
A B
E1
E4
E6
E7
E3
E5
E8
E2
(a) No, porque AB0
(b) No, porque P(A)*P(B)  P(AB)
3/8 * 5/8  2/8
(c) P(AB) = 2/8= 0,25
(d) P(A/B)= P(AB) / P(B)= (2/8) / (5/8)= 2/5
Esto puede verse en el diagrama, ya que
saber que B ocurrió, reduce nuestro espacio
muestral a los cinco elementos de B. Y de
ellos, sólo dos pertenecen a A.
Ejemplo

29. Problemas a resolver
Dos candidatos a los consejos de administración A y B, compiten por el
control de una corporación. Las probabilidades de ganar de estos
candidatos son 0,7 y 0,3, respectivamente. Si gana A, la probabilidad de
introducir un nuevo producto es 0,8; si gana B, la correspondiente
probabilidad es 0,4. Demuestre que, antes de las elecciones, la probabilidad
de que sea introducido un nuevo producto es 0,68.
A
B
N
Sugerencias: Recordar probabilidad condicional y probabilidad conjunta
Considerar todo el espacio muestral
Datos:
P(A)= 0,7 P(N/A)= 0,8
P(B)= 0,3 P(N/B)= 0,4
Solución:
P(N)= P(NA) + P(NB)
P(N)= P(N/A)*P(A) + P(N/B)*P(B)
P(N)= 0,8*0,7 + 0,4*0,3= 0,68
P(NA)
P(NB)

30. El 34% de las luminarias públicas de una ciudad tienen más de 5 años. El 54%
son de la Marca A. De los de la variedad A, el 7% tiene más de 5 años. Si se
elige una luminaria al azar,
a) ¿Cuál es la probabilidad de que tenga más de 5 años y sea de la Marca A?
b) ¿Cuál es la probabilidad de que teniendo menos de 5 años, sea de la Marca A?
1
0,66
0,34
0,46
0,1578
0,3022
Ā
0,54
0,5022
0,0378
A
<5
> 5
Datos:
P(>5)= 0,34 P(A)= 0,54
P(>5/A)= 0,07
Sugerencias: Recordar probabilidad condicional y probabilidad conjunta
Considerar tablas de contingencia
Solución:
a) P(>5A)= P(>5/A)*P(A) =
0,07*0,54= 0,0378
b) P(A/<5)= P(A<5) / P(<5)
= 0,5022 / 0,66= 0,76
Problemas a resolver