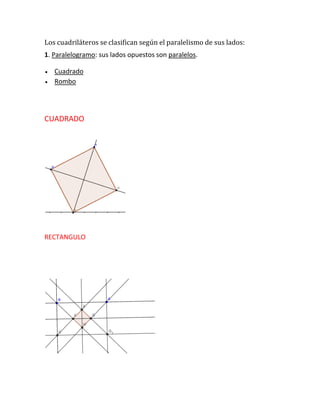
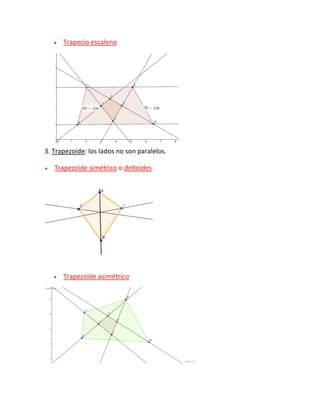
El documento define un cuadrilátero como un polígono de cuatro lados y clasifica los diferentes tipos de cuadriláteros basados en la forma de sus lados y ángulos. Explica que los cuadriláteros se dividen en simples y complejos, y que los simples incluyen paralelogramos, trapecios y trapezoides. También analiza cómo cambia la forma de un cuadrilátero cuando se trazan sus bisectrices.

1. Lopez Carolina
Aula: 004
Matematica I

2. RESOLUCION
Definición de cuadrilátero:
Un cuadrilátero es un polígono que tiene cuatro lados. Los
cuadriláteros pueden tener distintas formas, pero todos ellos
tienen cuatro vértices y dos diagonales, y la suma de sus ángulos
internos siempre da como resultado 360°.
Taxonomía de los cuadriláteros

3. En el gráfico ilustrativo de la taxonomía de los cuadriláteros se pasa de las
definiciones más generales a las más específicas siguiendo el sentido de
las flechas.
. En uno cuadrilátero simple los lados no se cruzan.
Los cuadriláteros simples se dividen en:

Cóncavos. En un cuadrilátero cóncavo al menos uno de sus ángulos
interiores mide más de 180°.

Convexos. Un cuadrilátero convexo no tiene ángulos interiores que midan
más de 180°. Los convexos se subdividen en:
1. Cuadrilátero cíclico, si se puede trazar una circunferencia que pase por
sus vértices.

4. 2. Cuadrilátero tangencial, si se puede trazar una circunferencia
tangente a cada uno de sus lados.
A un cuadrilátero que al mismo tiempo sea cíclico y tangencial se le
denomina cuadrilátero bicéntrico. El deltoide es tangencial con dos pares de
lados iguales.

5. Los cuadriláteros se clasifican según el paralelismo de sus lados:
1. Paralelogramo: sus lados opuestos son paralelos.


Cuadrado
Rombo
CUADRADO
RECTANGULO

6. Del rectángulo puedo concluir que al trazar sus bisectriz, obtengo un
cuadrado, compruebo que es, porque al trazar las bisectrices de este
cuadrilátero, se interceptan con el vértice opuesto.
ROMBOIDE
2. Trapecios: solo dos de sus lados son paralelos; los otros dos no.

Trapecio rectángulo

7. 
Trapecio isósceles

8. 
Trapecio escaleno
3. Trapezoide: los lados no son paralelos.

Trapezoide simétrico o deltoides

Trapezoide asimétrico

9. CUADRILATEROS COMPLEJOS

10. CUADRILATERO SIMPLE
CONCLUSION
Después de haber realizado, varios tipos de cuadriláteros puedo llegar a las
siguientes conclusiones:
No siempre queda determinado un nuevo cuadrilátero, al trazar las
bisectrices de este, como lo vemos en el caso del cuadrado, rombo,
cuadrilátero tangencial o trapecio simétrico que las bisectrices pasan

11. por el centro de la circunferencia, y algunos casos del trapecio
rectángulo.
Otra conclusión que se puede extraer es que, a trazar las bisectrices de
un cuadrilátero queda formado otro que tiene alagunas características
como se muestra en el siguiente cuadro:
cuadrilátero
Cuadrilátero
formado
por
bisectrices
Cuadrilátero cóncavo
Cuadrilátero convexo
Cuadrilátero cíclico
cíclico
rectángulo
rombo
romboide
rectángulo
Trapecio rectángulo
Trapezoide asimétrico
Trapecio isósceles
Simétrico o cíclico
Trapecio escaleno
Convexo
Trapecio asimétrico
escaleno
Cuadrilátero complejos
deltoides
Cuadrilátero simple
complejo
Comparando las áreas se puede inferir que cundo se trata de
uno complejo, el cuadrilátero resultante es de mayor área.
Con respecto al programa utilizado, no es fácil de usar al comienzo pero a
medida que se va trabajando con él se va haciendo más ameno, la
herramientas utilizadas fueron el trazado de paralelas, perpendiculares, un
intersección de dos objetos, segmento entre dos puntos, bisectrices,
tangentes, entre otros.