El documento es un problemario de análisis vectorial diseñado para ayudar a los estudiantes a comprender mejor la materia mediante la resolución de problemas. Incluye ejemplos que cubren álgebra de vectores, cálculo diferencial e integral vectorial, y se enfoca en conceptos fundamentales como gradiente, divergencia y rotacional. El autor menciona que la complejidad de la materia puede resultar desafiante para los estudiantes, y busca proporcionar un apoyo adicional para mejorar su comprensión y rendimiento.

1. Problemario de An´lisis Vectorial
a
Barranco Jim´nez Marco Antonio
e
e-mail: mabarrancoj@ipn.mx
June 24, 2004
1

2. 1 Introducci´n
o
La presente selecci´n de problemas resueltos de la materia de An´lisis Vectorial,
o a
tiene como objetivo principal, el de proporcionar al alumno que cursa la materia,
un apoyo bibliogr´fico m´s para el entendimiento de la misma, esperando que
a a
le sea de gran ayuda, en la aplicaci´n de la teoria adquirida en el sal´n de clases
o o
y poder ejercitar sus conocimientos en la soluci´n de problemas similares.
o
La mayoria de los problemas, son problemas que se resuelven como ejemplos
en el sal´n de clases tratando en lo que cabe de cubrir el m´s m´
o a ınimo detalle
algebraico, con la unica intenci´n de lograr la mejor comprensi´n por parte del
´ o o
alumno, como puede observarse en la soluci´n de cada problema. La mayoria
o
de los problemas resueltos, son problemas que est´n propuestos en libros tradi-
a
cionales de la materia, como por ejemplo, el libro de An´lisis Vectorial de la
a
editorial Mc Graw Hill (serie Schaum), cuyo autor es Murray R. Spiegel y el
libro de An´lisis Vectorial de la editorial Addison-Wesley Iberoamericana, cuyo
a
autor es Hwei P. Hsu., entre otros.
La idea de escribir esta serie de problemas, es debida principalmente a la ex-
periencia que el autor ha adquirido al impartir la materia en el primer semestre,
en la Escuela Superior de C´mputo del IPN, de la carrera de Ingenier´ en Sis-
o ıa
temas Computacionales, y en la cual el ´ ındice de alumnos que no aprueban la
materia es muy alto.
La materia de An´lisis Vectorial por si s´la, es una materia que generalmente
a o
es muy complicada para los estudiantes de nuevo ingreso, (a´n imparti´ndose
u e
´sta en un semestre posterior) en una carrera de Ingenier´ en el area de Cien-
e ıa ´
cias F´
ısico-Matem´ticas, este hecho tiene distintos puntos de vista; por ejemplo,
a
a a ´
los pocos conocimientos de las materias b´sicas de Matem´ticas ( Algebra, Ge-
ometr´ Anal´
ıa ıtica, C´lculo Diferencial e Integral, Trigonometr´ etc) con los que
a ıa,
cuenta el estudiante al ingresar al nivel superior, sin embargo, como el lector
podr´ observar, en la soluci´n de cada uno de los problemas resueltos, realmente
a o
son m´ınimos los conocimientos que el alumno necesita de las materias b´sicas de
a
Matem´ticas. As´ tambi´n, podr´ ser el desinter´s que muestran en general los
a ı e ıa e
alumnos hacia la materia, debido a que pos´ ıblemente las dem´s materias, como
a
Matem´ticas Discretas y Programaci´n, por mencionar algunas, son materias
a o
que en general los conceptos son m´s ”f´ciles” de entender por parte del alumno,
a a
o son materias de un inter´s mayor por ser materias dirijidas a su formaci´n.
e o
Y principalmente, en realidad el temario de la materia (mencionando tambi´n e
que en algunos casos puede ser muy extenso para cubrirse en un semestre, como
en muchas otras materias b´sicas), en general es dificil de asimilar por parte de
a
los alumnos, conceptos por ejemplo, por citar algunos, como el de Gradiente,
Divergencia y Rotacional, as´ como la parte de coordenadas curvil´
ı ıneas que in-
volucran el C´lculo de funciones de m´s de una variable, matem´ticamente son
a a a
complicados de manejar por los alumnos, sin mencionar la interpretaci´n f´ o ısica
de los mismos.
2

3. Este punto de vista puede o no ser compartida por muchos profesores que
imparten o han impartido alguna vez la materia, y es muy respetable su opini´n o
al respecto, sin embargo, como mencion´ anteriormente, la experiencia adquirida
e
al impartir la materia, me permiten hacer estas observaciones.
Los problemas se encuentran distribuidos de la siguiente forma:
En el cap´ ıtulo 1 se tratan problemas que comprenden lo relacionado al
´
Algebra de vectores; desde las operaciones b´sicas de vectores, algunos proble-
a
mas de aplicaci´n a la Geometr´ Anal´
o ıa ıtica, pasando por aplicaciones del pro-
ducto escalar y vectorial, dependencia lineal, triple producto escalar de vectores,
hasta ecuaciones de rectas y planos. En este cap´ ıtulo, se pone enf´sis en la
a
aplicaci´n de las propiedades elementales del producto escalar y vectorial entre
o
vectores, los cuales son conceptos b´sicos muy importntes enun curso tradicional
a
de la materia de An´lisis Vectorial.
a
En el cap´ıtulo 2 se tratan problemas relacionados con el C´lculo Diferencial
a
vectorial; desde el concepto de parametrizaci´n de curvas y superficies en el espa-
o
cio, derivaci´n de funciones vectoriales, aplicaciones de Gradiente, Divergencia
o
y Rotacional, hasta llegar a coordenadas curvil´ ıneas.
As´ mismo, en el cap´
ı ıtulo 3 se tratan problemas relacionados con el C´lculo
a
Integral vectorial, desde ejemplos de integrales de l´ ınea, integrales de superficie
e integrales de volumen, hasta llegar a problemas de aplicaci´n de los teoremas
o
integrales de Green, de Stokes y de Gauss.
Finalmente, como en cualquier tipo de trabajo, el lector tendr´ la ultima
a ´
palabra al decidir si se cumple el objetivo principal, as´ tambi´n, el autor esta
ı e
abierto a todo tipo de comentarios y sugerencias que ser´n bien venidas, para
a
la mejora del presente trabajo.
3

4. 2 Problemas del cap´
ıtulo 1.
Problema 1:
→
−
Muestre que para cualquier vector A = a1 i + a2 j + a3 k se cumple que:
→
−
a).− i× k× j× A = a3 k,
→
−
b).− k× j× i× A = a2 j,
→
−
c).− j× i× k× A = a1 i,
no aplique la definici´n del determinante, usar las propiedades del producto
o
vectorial.
Soluci´n:
o
a).− Aplicando las propiedades del producto vectorial, tenemos
→
−
i× k× j× A = i × k × j × a1 i + a 2 j + a 3 k
= i × k × j × a1 i + j × a2 j + j × a3 k
= i × k × −a1 k + a3 i
= i × −a1 k × k + a3 k × i
= i × a3 j
= a3 k.
b) De la misma forma,
→
−
k× j× i× A = k × j × i × a1 i + a 2 j + a 3 k
= k × j × i × a1 i + i × a2 j + i × a3 k
= k × j × a2 k − a 3 j
= k × j × a2 k + j × a3 j
= k × a2 i
= a2 j.
En forma an´loga para el inciso c).
a
4

5. Problema 2.
Probar que
→
− →
− →
− →
−
i × i × A + j × j × A + k × k + A = −2 A
→
−
donde A es cualquier vector en el espacio.
Soluci´n:
o
→
−
Sea el vector A en el espacio dado por,
→
−
A = ai + bj + ck,
→
−
sustituyendo el vector A y aplicando la propiedad distributiva del producto
vectorial, obtenemos
→
− −
→ →
−
i× i× A +j× j× A +k× k× A = i × i × ai + b j + c k
+ j × j × ai + b j + c k
+ k × k × ai + b j + c k
= i × i × ai + i × b j + i × ck +
j × j × ai + j × bj + j × ck +
k × k × ai + k × bj + k × ck ,
aplicando la definici´n del producto vectorial para los vectores i, j y k, y nue-
o
vamente aplicando la propiedad distributiva obtenemos,
→
− →
− →
−
i× i× A +j× j× A +k× k× A = i × bk − cj + j × −ak + ci + k × aj + bi
= bi × k − c i × j − aj × k + c j × i + ak × j − b k × i
= −bj − ck − ai − ck − ai − bj
finalmente, obtenemos
→
− →
− →
− →
−
i × i × A + j × j × A + k × k × A = −2ai − 2bj − 2ck = −2 A .
5

6. Problema 3.
Demostrar que el segmento que une los puntos medios de dos lados de un
tri´ngulo es paralelo al tercer lado y tiene la mitad de su longitud.
a
Soluci´n:
o
Consideremos un tri´ngulo cuyos v´rtices son los puntos A, B y C, como se
a e
muestra en la figura.
B
X
P Q
A C
Y
De la figura, obtenemos
−−
→ →
−
AB = X,
−→ →
−
AC = Y,
−→
− → →
− −
BC = Y − X,
por hip´tesis tenemos que,
o
−→
− 1→−
PB = X,
2
−→
− 1 → →
− −
BQ = ( Y − X ),
2
asimismo, de la figura en el tri´ngulo BP Q obtenemos,
a
−
−→ −→ −→
− −
P Q = P B + BQ
sustituyendo las ecuaciones anteriores,
−
−→ 1→ 1 → →
− − −
PQ = X + (Y − X)
2 2
1→−
= Y,
2
−
−→ →
− 1
de donde se deduce que P Q es paralelo a Y y tiene 2 de su longitud.
6

7. Problema 4.
−
−→ → −
Consideremos 3 puntos diferentes en el espacio O, P y Q, y sean OP = A ,
−→ →
− −
OQ = B y R el punto medio del segmento QP , demostrar como se ilustra en
→
− →
− → →
− −
la figura, que el vector C se puede escribir de la forma C = 1 A + B .
2
P
R
A
C
O Q
B
Soluci´n:
o
De la figura y por hip´tesis del problema se tiene que:
o
−
−→ −
−→
(1) QR = 1 QP ,
2
adem´s, aplicando la suma de vectores en el tri´ngulo OP Q,
a a
→ −
− −→ → −
(2) B + QP = A ,
y tambi´n de la figura, en el tri´ngulo OQR, obtenemos
e a
→ −
− −→ → −
(3) B + QR = C ,
sustituyendo la ecuaci´n (1) en la ecuaci´n (3),
o o
→ 1−
− −→ → −
(4) B + 2 QP = C ,
−
−→ → →− −
por otro lado de la ecuaci´n (2) QP = A − B , sustituyendo en la ecuaci´n (4)
o o
obtenemos,
→ 1 → →
− − − →
−
B+ A−B =C
2
apicando las propiedades distributiva y asociativa obtenemos,
→ 1 →
− − 1 →
− →
−
B+ A − B =C
2 2
1 →
− 1 →
− →
−
A + B =C
2 2
finalmente, obtenemos
→ 1 → →
− − −
C = A+B .
2
7

8. Problema 5.
Hallar el area del paralelogramo cuyas diagonales son los vectores,
´
→
−
A = 3i + j − 2k,
→
−
B = i − j + 4k,
Soluci´n:
o
→ →
− −
Geom´tricamente el producto vectorial de dos vectores A y B representa
e
→ →
− −
el area de un paralelogramo de lados A y B de la forma,
´
´ → →
− −
Area = A × B ,
A
x
B
y
en este caso, tenemos las diagonales del paralelogramo (ver figura), por lo que
necesitamos encontrar los lados del paralelogramo en t´rminos de las diagonales.
e
De la figura anterior, obtenemos
→
−
a) → + → = − B
− −
x y
→
−
b) → − → = A
− −
x y
sumamos las ecuaciones a) y b) obtenemos:
→ →
− −
2→ = A − B ,
−
x
de donde,
→ →
− −
c) → =
−
x 1
2 A−B ,
de forma an´loga restando la ecuaci´n b) de la ecuaci´n a), obtenemos
a o o
8

9. → →
− −
d) → = − 1 A + B .
−
y 2
De esta forma, de las ecuaciones c) y d), el area del paralelogramo est´
´ a
dada por:
´
Area = | → × →|
− −
x y
1 → →
− − 1 → →
− −
= A−B × − A+B
2 2
1 → →
− − → →
− −
= − A−B × A+B ,
4
aplicando las propiedades del producto vectorial tenemos,
´ 1 → →
− − →
− → →
− − →
−
Area = A − B × A + A − B × B.
4
1 → → → → → → → →
− − − − − − − −
= −A × A + A × B − B × A + B × B
4
1 → →
− −
= 2A × B
4
1 → →
− −
= A×B ,
2
finalmente al sustituir los vectores dados obtenemos,
1 i j k 1
´
Area = 3 1 −2 = 2i − 14j − 4k
2 2
1 −1 4
= i − 7j − 2k
√
= 1 + 49 + 4
√
= 54
√
= 3 6.
9

10. Problema 6.
Demostrar que las diagonales de un paralelogramo se cortan en su punto
medio.
Soluci´n:
o
Sea el paralelogramo de v´rtices A, B, C y D, como se ilustra en la siguiente
e
figura.
A B
y
x x
P
D C
y
De la figura, tenemos
−→
− → = −→
− −
DA = x CB,
−→
− →=−
− −→
DC = y AB,
asimismo, aplicando la suma de vectores
−→ → →
−
DB = − + − ,
x y
(1) −→ − −
AC = → − →,
y x
por otro lado de la definici´n de paralelismo
o
−→
− −→
−
DP = nDB,
(2) −→ −→
AP = mAC,
de las ecuaciones (1) y (2) obtenemos,
−→
−
DP = n (→ + →) ,
− −
x y
(3) − → → − →) ,
− −
AP = m ( y x
−→ −
− → −→−
por otro lado, en el tri´ngulo DAP, tenemos DA + AP = DP , es decir;
a
10

11. (4) → + − = −→,
→
− AP DP
x
−
sustituyendo las ecuaciones (3) en la ecuaci´n (4) obtenemos,
o
→ + m (→ − →) = n (→ + →) ,
−
x − −
y x − −
x y
aplicando las propiedades de la adici´n de vectores obtenemos,
o
→ + m → − m→ − n → − n → = →,
−
x −
y −
x −
x −
y
−
0
o tambi´n,
e
−
→
(1 − m − n)→ + (m − n)→ = 0 ,
−
x −
y
→
−
de la ecuaci´n anterior, como los vectores → y → son distintos del vector 0
o −
x −
y
y no paralelos, entonces la igualdad anterior s´lo se cumple si los escalares son
o
iguales a cero, es decir;
1−m−n = 0,
m−n = 0,
resolviendo el sistema de ecuaciones para n y m obtenemos,
1
n=m= ,
2
por lo tanto, sustituyendo en las ecuaciones (2) obtenemos
−→
− 1 −→
−
DP = DB,
2
−→ 1− →
AP = AC.
2
Como se ilustra geom´tricamente en la figura.
e
11

12. Problema 7.
Demostrar que las medianas de un tri´ngulo se cortan en un punto que esta
a
3
2
a 1 del lado y 3 del v´rtice opuesto para cada mediana respectivamente.
e
Soluci´n:
o
Sea el tri´ngulo cuyos v´rtices son A1 , B1 y C1 . Asimismo sean A2 , B2 y C2
a e
los puntos medios de cada lado respectivamente, como se ilustra en la figura. Si
P es el punto de intersecci´n de las medianas, entonces para demostrar que las
o
1
medianas se cortan en un punto que esta a 3 del lado y 2 del v´rtice opuesto
3 e
para cada mediana debemos mostrar que se cumplen las siguientes relaciones:
B1
A 2
A C2 P
C1
B2
A1
B
−→
− 2− −
−→
A1 P = 3 A1 A2 ,
−→
− 2 −→
−−
B1 P = 3 B1 B2 ,
(a)
−→
− 2− −
−→
C1 P = 3 C1 C2 ,
o equivalentemente,
−→
− 1− −
−→
P A2 = 3 A1 A2 ,
−→
− 1 −→
−−
P B2 = 3 B1 B2 ,
(b)
−→
− 1− −
−→
P C2 = 3 C1 C2 ,
como se ilustra geom´tricamente en la figura. Sean los lados del tri´ngulo dados
e a
→ →
− −
por A y B , de la figura tenemos las siguientes relaciones:
→
− −−
−→
A = A1 B 1 ,
→
− −−
−→
B = A1 C1 ,
→ →
− − −−
−→
B−A = B 1 C1 .
12

13. Aplicando la definici´n de paralelismo, de la figura obtenemos
o
−→
− −−
−→
A1 P = l A1 A2 ,
−→
− −−
−→
B1 P = m B1 B2 , (c)
−→
− −−
−→
C1 P = n C1 C2 ,
por otro lado, aplicando la suma y diferencia de vectores en los tri´ngulos
a
A1 C1 P, B1 C1 P y A1 B1 P obtenemos,
→ −→ −→
− − −
B + C1 P = A1 P ,
→ →
− − −→ −→
− −
B − A + C1 P = B 1 P , (d)
→ →
− − −→ −→
− −
B − A + C1 P = B 1 P ,
pero, de la figura tenemos tambi´n las siguientes relaciones
e
−−
−→ → − → →
− − 1 →− →
−
A1 A2 = A + 1 B − A = 2 A + B ,
2
−−
−→ → →
− − (e)
B1 B2 = 1 B − A ,
2
− → 1→ →
−− − −
C1 C2 = 2 A − B ,
que resultan de aplicar la suma y diferencia de los vectores en los tri´ngulos
a
A1 B1 A2 , A1 C1 C2 y A1 B1 B2 respectivamente. De las ecuaciones (a) y (b) se
obtiene,
→
− −−
−→ −−
−→
B + n C1 C2 = l A1 A2 ,
→ →
− − −−
−→ −−
−→
B − A + n C1 C2 = m B 1 B 2 , (f )
→
− −−
−→ −−
−→
A + m B 1 B 2 = n A1 A2 ,
sustituyendo las ecuaciones (e) en las ecuaciones (f ) obtenemos,
→
− → →
− − − →
→ −
B +n 1B − A =l 1 A + B
2 2 ,
→ →
− − 1→
− → − 1→
− →−
B − A +n 2B − A =m 2B − A , (g)
→
− 1→
− → − → →
− −
A +m 2B − A = n A + B ,
2
aplicando las propiedades de la suma de vectores, obtenemos
13

14. n l →
− l →
− →
−
− A + 1−n− B = 0,
2 2 2
n →
− m →
− →
−
m+ −1 A + 1−n− B = 0,
2 2
l →
− n l →
− →
−
1−m− A+ − B = 0.
2 2 2
− →
→ −
Por lo tanto, como A y B son vectores distintos de cero, entonces para que
se cumplan las ecuaciones anteriores los escalares deben ser cero, es decir;
n l
− = 0
2 2
l
1−n− = 0
2
n
m+ −1 = 0
2
m
1−n− = 0
2
l
1−m− = 0
2
n l
− = 0
2 2
as´ al resolver las ecuaciones anteriores obtenemos
ı,
2
n=l=m= .
3
Finalmente, al sustituir en las ecuaciones (c) se obtienen las ecuaciones (a)
que es el resultado que se pedia demostrar.
14

15. Problema 8.
→ →
− − → →
− − → →
− − → →
− −
Pruebe que A B + B A es perpendicular a A B − B A , para cua-
→ →
− −
lesquiera A y B .
Soluci´n:
o
De la definici´n del producto escalar de dos vectores, si dos vectores →
o −
x
→ son perpendiculares entonces su producto escalar entre ellos es igual a
−
y y
→ →
− − → →
− −
cero, en este caso → y → est´n dados respectivamente por A B + B A y
−
x −
y a
→ → → →
− − − −
A B − B A , de esta forma debemos verificar que los vectores dados cumplen
que,
→·→=
− − → →
− − − −
→ → → →
− − → →
− −
x y A B+ B A · A B − B A = 0,
aplicando la propiedad distributiva del producto escalar tenemos,
→·→=
− − → →
− − → →
− − → →
− − → →
− − → →
− − → →
− −
x y A B+ B A · A B+ A B+ B A · − B A ,
asimismo, aplicando las propiedades conmutativa y distributiva nuevamente,
tenemos
→ · → = − → · → → + → → · → → − → → · → → − → → · → →,
− −
x y
→ − − −
A B A B
− − − −
A B B A
− − − −
B A A B
− − − −
B A B A
ahora aplicamos las propiedades asociativa del escalar y la propiedad de la
norma,
→·→
− − → → → →
− − − − → → → →
− − − − → → → →
− − − − → → → →
− − − −
x y = A A B·B+ A B B·A− B A A·B− B B A·A
→ →
− − → →
− −
= A2 B 2 + AB B · A − AB A · B − B 2 A2
= 0.
donde se aplic´ finalmente la propiedad conmutativa del producto escalar.
o
15

16. Problema 9.
Demostrar que la suma de los cuadrados de las diagonales de un paralelo-
gramo es igual a la suma de los cuadrados de sus lados.
Soluci´n:
o
Sean A, B, C y D los v´rtices del paralelogramo como se indica en la figura.
e
C Y
D
X
X
A B
Y
De la figura tenemos que,
→
−
AC = BD = X ,
→
−
AB = CD = Y ,
asimismo de la figura, las diagonales del paralelogramo est´n dadas por
a
→ →
− −
BC = X+Y ,
→ →
− −
AD = X−Y .
Debemos mostrar que,
2 2 2 2 2 2
BC + AD = AC + AB + CD + BD
2 2
= 2AC + 2AB ,
es decir,
16

17. → →
− − 2 → →
− − 2 →
− 2 →2
−
X+Y + X−Y =2 X +2 Y .
En forma an´loga, al problema anterior, aplicando las propiedades del pro-
a
ducto escalar,
→ →
− − 2 → →
− − 2 → →
− − → →
− − → →
− − → →
− −
X+Y + X−Y = X+Y · X+Y + X−Y · X−Y
→ → →
− − − → → →
− − − → → →
− − − → → →
− − −
= X+Y ·X + X+Y ·Y + X −Y ·X+ X−Y ·Y
→ → → → → → → → → → → → → → → →
− − − − − − − − − − − − − − − −
= X·X +X·Y +X·Y +Y ·Y +X ·X−X·Y −X·Y +Y ·Y
− −
→ → − −
→ →
= 2X · X + 2 Y · Y
→2
− →2
−
= 2 X +2 Y .
17

18. Problema 10.
→ →
− − →
− →
− →
− →
−
Sean los vectores A y B vectores unitarios, calcular 3 A − 4 B · 2 A + 5 B
→ →
− − √
si A + B = 2.
Soluci´n:
o
En forma an´loga al problema anterior, aplicando las propiedades del pro-
a
ducto escalar , tenemos que
→
− →
− →
− →
− →
− →
− →
− →
− →
− →
−
3A − 4B · 2A + 5B = 3A − 4B · 2A + 3A − 4B · 5B
→ →
− − → →
− − → →
− − → →
− −
= 2A · 3A − 2A · 4B + 5B · 3A − 5B · 4B
→ →
− − → →
− − → →
− −
= 6 A · A + 7 A · B − 20 B · B
→ →
− −
= 7 A · B − 14
→ →
− −
donde se aplic´ la hip´tesis de que los vectores A y B son unitarios es decir
o o
que cumplen que,
→ →
− −
A·A = A2 = 1,
→ →
− −
B·B = B 2 = 1.
→ →
− − √
Por otro lado, de la condici´n A + B = 2, elevando al cuadrado ´sta
o e
expresi´n y aplicando la la propiedad de la norma del producto escalar, obten-
o
emos
→ →
− − → →
− −
A+B · A+B =2
de donde,
− −
→ → → − → → →
− − −
A+B ·A+ A+B ·B = 2
→ →
− − → → → →
− − − −
A · A + 2A · B + B · B = 2
→ →
− −
de la expresi´n anterior, obtenemos inmediatamente que A · B = 0. Por lo
o
tanto, sustituyendo este valor, obtenemos finalmente,
→
− →
− →
− →
−
3 A − 4 B · 2 A + 5 B = −14.
18

19. Problema 11.
→
− →
− →
−
Determine λ1 y λ2 de manera que C − λ1 A − λ2 B sea perpendicular tanto
→
− →
−
a A como a B , suponiendo que
→
−
A = i + j + 2k
→
−
B = 2i − j + k
→
−
C = 2i − j + 4k
Soluci´n:
o
En forma an´loga al problema anterior, aplicando la condici´n de perpen-
a o
dicularidad entre vectores, tenemos
→ →
− − →
− →
−
A · C − λ1 A − λ2 B = 0,
→ →
− − →
− →
−
B · C − λ1 A − λ2 B = 0,
usando las propiedades del producto escalar, tenemos
→ →
− − → →
− − → →
− −
A · C − λ1 A · A − λ2 A · B = 0,
→ →
− − → →
− − → →
− −
B · C − λ1 B · A − λ2 B · B = 0,
que se puede escribir de la forma,
→ →
− − → →
− − → →
− −
λ1 A · A + λ 2 A · B = A · C,
→ →
− − → →
− − → →
− −
λ1 B · A + λ 2 B · B = B · C,
de los vectores dados, tenemos inmediatamente aplicando la definici´n del pro-
o
ducto escalar para vectores en el espacio,
→ →
− − → →
− − → → → →
− − − − → →
− − → →
− −
A · A = 6, B ·B =6 A · B = B · A = 3, A·C =9 y B ·C =9
de tal forma, para encontrar λ1 y λ2 debemos de resolver el siguiente sistema
de ecuaciones:
19

20. 6λ1 + 3λ2 = 9,
3λ1 + 6λ2 = 9,
obs´rvese que la soluci´n del sistema de ecuaciones es inmediata y est´ dada
e o a
por:
λ1 = 1
λ2 = 1.
20

21. Problema 12.
Sean los vectores
→
−
A = (1, −1, 2),
→
−
B = (1, 2, 2).
→
− →
−
Hallar la proyecci´n del vector A sobre el vector B y la proyecci´n del vector
o o
→
− →
−
B sobre el vector A .
Soluci´n:
o
Por definici´n, la proyecci´n de un vector → sobre otro vector →, es un
o o −x −
y
vector (como se muestra en la figura) y est´ dado por,
a
y
−
Pr oy→ → = |→| cos θe→ ,
− x
−
x −
y
X
e→
−
y Pr oy→ →
−
− x
y
→
−
y
en este caso debemos calcular,
→
− →
−
Pr oy→ A
−
B
= A cos θe→ ,
−
B
→
− →
−
Pr oy→ B
−
A
= B cos θe→ ,
−
A
→
− → →
− − →
−
donde A es la magnitud del vector A , B es la magnitud del vector B , θ el
21

22. angulo formado entre los dos vectores, e→ un vector unitario en la direcci´n del
´ −
A
o
→
− →
−
→ un vector unitario en la direcci´n del vector B . De la definici´n
vector A y e B
− o o
del producto escalar podemos calcular el coseno del angulo entre dos vectores
´
de la forma,
→ →
− −
A·B
cos θ = → → ,
− −
A B
y empleando la definici´n de vectores unitarios, los vectores de proyecci´n est´n
o o a
dados por,
 
→ →
− − →
− → →
− −
→
− →  A·B
−  B = A·B →
−
Pr oy→ A
− = A → →
− − →
− B,
B
A B B B2
 
→ →
− − →
− → →
− −
→
− →  A·B
−  A = A·B →
−
Pr oy→ B
− = B → →
− − →
− A,
A
A B A A2
finalmente, calculando el producto escalar de los vectores dados y la magnitudes
→ →
− −
de los vectores A y B , obtenemos
→ 3→ 1→
− − −
Pr oy→ A = B = B ,
−
B 9 3
y
→ 3→ 1→
− − −
Pr oy→ B = A = A .
−
A 6 2
22

23. Problema 13:
Considere la siguiente figura,
A A2
A1 B
demostrar que
→ →
− − → →
− − →
−
→
− A ·B→
− B×A ×B
A = → →B +
− − → →
− − .
B·B B·B
Soluci´n:
o
→ →
− − →
− →
−
De la figura, el vector A = A 1 + A 2 , el vector A 1 es la proyeccci´n del
o
→
− →
−
vector A sobre el vector B dada por
→
− →
− →
−
A 1 = proy→ A = A cos θe→ ,
−
B
−
B
→ →
− −
de la definici´n del producto escalar de dos vectores A y B distintos del vector
o
→
−
0 , dada por,
→ →
− − − −
→ →
A · B = A B cos θ,
podemos calcular el angulo entre los dos vectores, de esta forma la proyecci´n
´ o
→
− →
−
del vector A sobre el vector B est´ dada por:
a
23

24.  
→ →
− − →
−
→
− →  A·B  B
−
proy→ A
−
B
= A → −
− → →
−
A B B
→ →
− −
A ·B→
−
= B
→2
−
B
→ →
− −
A ·B→
−
= → → B,
− −
B·B
→
−
donde se aplic´ la propiedad de la norma del producto escalar. Para vector A 2 ,
o
→ → →
− − − →
−
obs´rvese que el vector C = B × A es perpendicular tanto al vector A como
e
→
− → →
− −
al vector B , es decir, saliendo de la hoja, de tal forma que el vector C × A ser´
a
→
− → →
− − →
−
un vector que est´ en la direcci´n de A 2 , es decir, el vector B × A × A esta
a o
−
→
en direcci´n de A , de tal forma que la magnitud de este vector est´ dada por:
o a
→ →
− − →
− − − −
→ → →
B × A × B = B × A B sin φ,
→ →
− − →
−
donde el angulo φ entre los vectores B × A y B es de 900 , de esta forma
´
como sin 900 = 1, obtenemos
− −
→ → −
→ → →
− − →
−
B × A × B = B A sin θ B ,
es decir,
→ →
− − →
− → →2
− −
B × A × B = A B sin θ,
por otro lado, de la figura
→
− →
−
A 2 = A sin θ,
por lo tanto,
→ →
− − →
−
→
− B×A ×B
A2 = → →
− − ,
B·B
→
− →
−
finalmente, sustituyendo los valores de los vectores A 1 y A 2 obtenemos,
24

25. → →
− − → →
− − →
−
→
− A ·B→
− B×A ×B
A = → →B +
− − → →
− − .
B·B B·B
25

26. Problema 14.
Encuentre un vector unitario perpendicular a los vectores
→
−
A = 2i + 2j − 3k,
→
−
B = i + 3j − k,
a) Aplicando el producto escalar.
b) Aplicando el producto vectorial (sin hacer uso de la definici´n del deter-
o
minante).
Soluci´n:
o
→
−
a) Debemos encontrar un vector C = (C1 , C2 , C3 ) que sea perpendicular a
→ →
− −
los vectores A y B simult´neamente, es decir que cumpla que,
a
→ →
− −
A·C = 0,
→ →
− −
B·C = 0,
realizando el producto escalar de los vectores dados obtenemos,
2C1 + 2C2 − 3C3 = 0,
C1 + 3C2 + C3 = 0,
resolviendo el sistema de ecuaciones (multiplicando la segunda ecuaci´n por −2
o
y sum´ndo ´sta con la primera ecuaci´n) obtenemos,
a e o
−4C2 − 5C3 = 0,
de donde,
−5
C2 = C3 ,
4
sustituyendo este valor para C2 ,en por ejemplo la segunda ecuaci´n, obtenemos
o
−5
C1 = −3 C3 − C3
4
11
= C3 .
4
De esta forma, el vector buscado tiene la forma,
→ 11
− 5
C = C3 i − C3 j + C3 k,
4 4
26

27. →
−
adem´s el vector buscado, C , debe cumplir que sea unitario, es decir que cumpla
a
que,
→
−
C = 1,
aplicando la definici´n para calcular la magnitud de un vector, obtenemos
o
2 2
11 5 2
C3 + C3 + C3 = 1
4 4
2
C3
(121 + 25 + 16) = 1
16
√
2 162
C3 = 1
4
despejando C3 , obtenemos
4 4
C3 = ± √ =± √
162 9 2
→
−
finalmente, al sustituir el valor de C3 , en la expresi´n para el vector C , obten-
o
emos
→
− 1
C = ± √ (11i − 5j + 4k)
9 2
b) En esta parte, como se nos pide que no hagamos uso del determinante
→ → →
− − −
para calcular el producto vectorial, que como se sabe C = A × B , es un vector
→
− →
−
que por definici´n es perpendicular tanto a A como a B , debemos emplear
o
las propiedades (anticonmutativa, asociativa, distributiva, etc.) que cumple el
producto vectorial, por lo tanto
→ →
− −
A×B = (2i + 2j − 3k) × (i + 3j + k)
= (2i + 2j − 3k) × i + (2i + 2j − 3k) × (3j) + (2i + 2j − 3k) × k
= −i × (2i + 2j − 3k) − 3j(2i + 2j − 3k) − k × (2i + 2j − 3k)
= −2 × i − 2i × j + 3j × k − 6j × i − 6j × j + 9j × k − 2k × i − 2k × j + 3k × k
= −2k − 3j + 6k + 9i − 2j + 2i
= 11i − 5j + 4k,
finalmente, el vector unitario estar´ dado por:
a
27

28. → →
− −
A×B 11i − 5j + 4k 1
e→×→
− −
A B
= → → = √
− − = ± √ 11i − 5j + 4k .
A×B 121 + 25 + 16 9 2
28

29. Problema 15.
→
−
Hallar un vector unitario que forme un angulo de 45 ◦ con el vector A =
´
→
−
2i + 2j − k y un angulo de 60◦ con el vector B = j − k.
´
Soluci´n:
o
→
− →
−
Buscamos un vector de la forma C = (C1 , C2 , C3 ) donde el vector C debe
cumplir,
→ →
− −
A·C = AC cos 45◦
→ →
− −
B·C = BC cos 60◦
y
→
−
C =1
es decir,
2 1
2 i + 2 j − k · C1 i + C 2 j + C 3 k = 22 + 22 + (−1) √
2
2 1
j − k · C1 i + C 2 j + C 3 k = 12 + (−1)
2
2 2 2
(C1 ) + (C2 ) + (C3 ) = 1
que resulta,
3
(1) 2C1 + 2C2 − C3 = √
2
√
2
(2) C 2 − C3 = 2
2 2 2
(3) (C1 ) + (C2 ) + (C3 ) = 1
as´ se tienen 3 ecuaciones con 3 incognitas. Por lo tanto, la soluci´n del prob-
ı, o
lema se tendr´ al resolver simult´neamente las √
a a ecuaciones (1), (2) y (3).
De la ecuaci´n (2), obtenemos C3 = C2 − 22 , sustituyendo en la ecuaci´n
o o
(1) obtenemos,
√
2 3
2C1 + 2C2 − C2 − = √
2 2
1 3
2C1 + 2C2 − C2 + √ = √
2 2
2
2C1 + C2 = √
2
29

30. finalmente, obtenemos
1 C2
C1 = √ − .
2 2
→
−
Por lo tanto el vector C ser´ de la forma,
a
→
− 1 C2 1
4) C = √
2
− 2 i + C 2 j + C2 − √
2
k,
aplicando la ecuaci´n (3),
o
2 2
1 C 1
√ − 2 2
+ (C2 ) + C2 − √ = 1,
2 2 2
realizando un poco de algebra se obtiene,
´
2
1 1 C2 (C2 ) 2 2 1 1
−2 √ + + (C2 ) + (C2 ) − 2C2 √ + = 1
2 2 2 4 2 2
2
1 C2 (C2 ) 2 2 1 1
−√ + + (C2 ) + (C2 ) − 2C2 √ + = 1
2 2 4 2 2
9 2 3
(C2 ) − √ C2 = 0
4 2
√
3 3 2
√ C2 C2 − 1 = 0
2 4
por lo tanto las soluciones para C2 son:
C21 = 0,
y
4
C22 = √ ,
3 2
sustituyendo en la ecuaci´n (4) finalmente obtenemos,
o
→
− 1 1 1 1
C1 = √ i+ √ k = √ , 0, − √ ,
2 2 2 2
y
30

31. −
→ 1 1 4 4 4 1
C2 = √ − √ i+ √ j+ √ −√ k
2 2 3 2 3 2 3 2 2
1 4 1
= √ i+ √ j+ √ k
3 2 3 2 3 2
1 4 1
= √ , √ , √
3 2 3 2 3 2
31

32. Problema 16.
Escriba un vector de magnitud 5, paralelo al plano 3x + 4y + 5z = 10 y
perpendicular al vector i + 2j + 2k.
Soluci´n:
o
→
−
Se pide un vector de la forma C = C1 i + C2 j + C3 k que sea paralelo al
→
−
plano 3x + 4y + 5z = 10 y perpendicular al vector A = i + 2j + 2k, es decir,
que cumpla las siguientes condiciones:
→ →
− −
C · A = 0,
→ →
− −
C · N = 0,
→
−
donde N = 3i + 4j + 5k, es el vector normal al plano. Calculando los productos
escalares, las condiciones anteriores se pueden escribir de la forma,
C1 + 2C2 + 2C3 = 0,
3C1 + 4C2 + 5C3 = 0,
resolviendo simult´neamente las ecuaciones anteriores obtenemos,
a
C1 = 2C2 ,
C3 = −2C2,
→
−
por lo tanto, el vector C ser´ de la forma,
a
→
−
C = 2C2 i + C2 j − 2C2 k,
y aplicando la condici´n de que el vector debe ser de magnitud 5, es decir
o
→
−
C = 5, obtenemos
5 = 2 2 2
4C2 + C2 + 4C2
= 2
9C2
= ±3C2 ,
32

33. de donde,
5
C2 = ± ,
3
finalmente, el vector pedido es de la forma,
→
− 5
C =± 2i + j − 2 k .
3
33

34. Problema 17.
Hallar un vector unitario paralelo al plano XY y perpendicular al vector
4i − 3j − k.
Soluci´n:
o
→
− →
−
Se pide un vector C de la forma, C = C1 i + C2 j, la componente C3 es
→
−
cero debido a que el vector C debe ser paralelo al plano XY y por lo tanto
→
−
no tiene componente en k, adem´s el vector C debe ser perpendicular al vector
a
→
−
A = 4i − 3j − k, por lo tanto cumple la condici´n,
o
→ →
− −
C · A = 0,
es decir,
C1 i − C2 j · 4i − 3j − k = 0,
de donde obtenemos,
3
C1 = C2 .
4
→
−
Por lo tanto, el vector pedido tendr´ la forma C = 3 C2 i + C2 j. Tambi´n
a 4 e
→
−
por hip´tesis, se pide que el vector C sea unitario, es decir que cumpla que
o
→
−
C = 1, por lo tanto
2
→
− 3 2 2 9 5
1= C = C2 + (C2 ) = (C2 ) 1+ = ± C2 ,
4 16 4
de donde, obtenemos
4
C2 = ± ,
5
y
3 4 3
C1 = ± =± ,
4 5 5
finalmente, el vector pedido est´ dado por,
a
→
− 3 4
C = ± i ± j.
4 5
34

35. Problema 18.
a) Hallar un vector unitario que forme un angulo de 30 0 con el vector j y
´
√
formando angulos iguales con los vectores i y k cos 300 = 23 .
´
Soluci´n:
o
→
−
El vector que estamos buscando es de la forma C = (C1 , C2 , C3 ) donde el
→
−
vector C debe cumplir que,
→
− →
−
1) C · i = C i cos θ = cos θ,
→
− →
−
2) C · k = C k cos θ = cos θ,
→
− →
−
3) C · j = C j cos 300 = cos 300 ,
por definici´n de los vectores unitarios i = (1, 0, 0), j = (0, 0, 1) y k = (0, 0, 1),
o
aplicando la definici´n del producto escalar para vectores en el espacio, y de
o
las ecuaciones 1) y 2) obtenemos,
C1 = C 3 ,
asimismo de la ecuaci´n 3), se tiene
o
√
3
C2 = ,
2
sustituyendo las ecuaciones anteriores, el vector pedido tiene la forma,
√
→
− 3
C = C1 , , C1 ,
2
para encontrar la componente C1 aplicamos la condici´n de que tiene que ser el
o
→
− →
−
vector C unitario, es decir, C = 1, de esta forma
√ 2
2
3
C1 + + C1 2 = 1,
2
de donde obtenemos,
1
C1 = ± √ ,
8
por lo tanto, el vector pedido tiene la forma,
√
→
− 1 3 1
C =± √ , ,√ .
8 2 8
35

36. Problema 19.
Siendo el vector de posici´n → de un punto dado (x0 , y0 , z0 ) y → el vector
o −a −r
de posici´n de un punto cualquiera (x, y, z), hallar el lugar geom´trico de → si:
o e −
r
a).− (→ − →) · → = 0
− − −
r a a
→ − →) · → = 0
− − −
b).− ( r a r
Soluci´n:
o
a) Sean los vectores
→
−
a = (x0 , y0 , z0 ),
→
−
r = (x, y, z),
entonces,
(→ − →) · → = 0,
− − −
r a a
(x − x0 , y − y0 , z − z0 ) · (x0 , y0 , z0 ) = 0,
x0 (x − x0 ) + y0 (y − y0 ) + z0 (z − z0 ) = 0,
si hacemos d = x2 + y0 + z0 , la ecuaci´n anterior se puede escribir de la forma,
0
2 2
o
x0 x + y0 y + z0 z = d,
que es la ecuaci´n de un plano que pasa por un extremo del vector → y es
o −
a
perpendicular al vector →.
−
a
En forma an´loga al inciso a), tenemos
a
(→ − → ) · → = 0
− − −
r a r
x(x − x0 ) + y(y − y0 ) + z(z − z0 ) = 0,
x2 + y0 + z0 − xx0 − yy0 − zz0 = 0,
0
2 2
completando cuadrados en la expresi´n anterior, obtenemos
o
x0 2 y0 z0 1
(x − ) + (y − )2 + (z − )2 = (x2 + y0 + z0 ),
2 2
2 2 2 4 0
que es la ecuaci´n de una esfera con centro en el punto x0 , y0 , z2
o 2 2
0
y radio
1
r= 2 0
2 2
x2 + y0 + z 0 .
36

37. Problema 20.
ınea recta x − 1 =
Determine el angulo entre el plano x + y + z = 21 y la l´
´
y + 2 = 2z + 3.
Soluci´n:
o
Sabemos que la ecuaci´n ax + by + cz = d, es la ecuaci´n de un plano que
o o
→
−
pasa por un punto y tiene como normal al vector N = (a, b, c) , asimismo, la
ecuaci´n x−x0 = y−y0 = z−z0 , representa la ecuaci´n de una l´
o a1 b1 c1 o ınea recta que
→ = (x , y , z ) y es paralela al vector → = (a , b , c ) , por
−
pasa por el punto r
−
A
0 0 0 0 1 1 1
lo tanto, para calcular el angulo entre el plano y la l´
´ ınea recta es equivalente a
→
− →
−
calcular el angulo entre los vectores N y A . En este caso, para el plano dado
´
→
−
tenemos que el vector normal est´ dado por N = (1, 1, 1) y para identificar el
a
vector paralelo a la recta dada, reescribimos la ecuaci´n de la recta de la forma,
o
3
x−1 y − (−2) z − (− 2 )
= = 1
1 1 2
de donde, obtenemos
→
−
r0 = (−1, −2, −3/2) ,
→
−
A = (1, 1, 1/2).
−
→ −
→
Para obtener el angulo entre los vectores N y A , aplicamos la definici´n
´ o
del producto escalar de dos vectores dado por,
→ →
− − → →
− −
N · A = N A cos θ,
de donde,
 
→ →
− −
−1  A •N 
θ = cos → → ,
− −
A N
→
− →
−
sustituyendo los vectores A y N , obtenemos
 
(1, 1, 1/2) · (1, 1, 1)
θ = cos−1  
1
(1)2 + ( 2 )2 (1)2 + (1)2 + (1)
 
5/2 
θ = cos−1 
27
4
5
= cos−1 √ .
3 3
37

38. Problema 21.
Encuentre una combinaci´n lineal (si existe) para los siguientes vectores:
o
−
→
A1 = −2i + 12j − 4k,
−
→
A2 = i − 6j + 2k,
−
→
A3 = 2j + 7k,
Soluci´n:
o
Para verificar si existe una combinaci´n lineal entre los vectores, debemos
o
encontrar escalares x, y y z para verificar si al menos uno de ´stos escalares es
e
distinto de cero, tal que se cumpla que:
−
→ −
→ −
→ → −
x A1 + y A2 + z A3 = 0 ,
es decir,
x(−2, 12, −4) + y(1, −6, 2) + z(0, 2, 7) = (0, 0, 0)
(−2x + y, 12x − 6y + 2z, −4x + 2y + 7y) = (0, 0, 0)
aplicando igualdad de vectores en el espacio (dos vectores son iguales si son
iguales componente a componente), obtenemos el siguiente sistema de ecua-
ciones,
−2x + y = 0,
12x − 6y + 2z = 0,
−4x + 2y + 7z = 0.
Al resolver este sistema de ecuaciones (se obtiene la soluci´n si se aplica, por
o
ejemplo el m´todo de Gauss), el sistema es equivalente al sistema,
e
−2x + y = 0
z = 0
la soluci´n del sistema anterior, es de la forma
o
y = 2x,
x = α∈R
z = 0
es decir, la soluci´n del sistema es la terna,
o
(x, y, z) = (α, 2α, 0) = α(1, 2, 0),
38

39. para toda α ∈ R, as´ por ejemplo si α = 1, entonces una soluci´n del sistema
ı o
ser´ de la forma,
a
x = 1,
y = 2,
z = 0,
− −
→ → − →
por lo tanto, la combinaci´n lineal de los vectores A1 , A2 y A3 est´ dada por:
o a
−
→ −
→ −
→ → −
A1 + 2 A2 + 0 A3 = 0
o tambi´n
e
→
− −
→
A1 = −2A2 .
39

40. Problema 22.
Encuentre una combinaci´n lineal (si existe) de los vectores
o
→
−
A = 2ˆ +  − 3k,
ı ˆ
→
−
B = ˆ − 2ˆ − 4k,
ı 
→
−
C = 4ˆ + 3ˆ − k,
ı 
Soluci´n:
o
Verifiquemos primeramente si los vectores son l.i. o l.d., para esto apliquemos
la propiedad del producto triple escalar que establece la condici´n necesaria para
o
→ → →
− − −
la dependencia lineal, es decir; si A • B × C = 0, entonces los vectores est´n a
en un plano y son linealmente dependientes, de esta forma,
2 1 −3
→ → →
− − −
A•B×C = 1 −2 −4
4 3 −1
= 2 (2 + 12) − 1 (−1 + 16) − 3 (3 + 8)
= 2 (14) − 1 (15) − 3 (11)
= 28 − 15 − 33
= −20,
− −
→ → → − − −
→ → −
→
de lo anterior, como A • B × C = 0, entonces los vectores A , B y C son
linealmente independientes, y por lo tanto, no existe combinaci´n lineal de ellos.
o
40

41. Problema 23.
Encontrar un vector unitario perpendicular a la l´
ınea recta dada por las
ecuaciones param´tricas,
e
x = 2t − 1,
y = −t − 1,
z = t + 2,
y perpendicular al vector i − j.
Soluci´n:
o
Las ecuaciones param´tricas de la recta dada son equivalentes a la ecuaci´n
e o
vectorial
→(t) = → + t→,
−
r −
r0
−
A
que representa a una recta L en forma param´trica que pasa por el punto →0 =
e −r
→
−
(−1, −1, 2) y que es paralela al vector A = (2, −1, 1).
→
−
Se pide un vector de la forma C = C1 i+C2 j +C3 k que tenga magnitud uno,
→
−
adem´s que sea perpendicular a la recta →(t) = → +t A , es decir perpendicular
a −r −r0
−
→ −
→
al vector A , y tambi´n perpendicular al vector B = i − j, es decir, que cumpla
e
las siguientes condiciones:
−
→
1) C = 1,
− −
→ →
2) C · A = 0,
→ →
− −
3) C · B = 0,
de las condiciones 2) y 3), calculando el producto escalar, obtenemos
2C1 − C2 + C3 = 0,
C1 − C 2 = 0,
de donde obtenemos inmediatamente que,
C1 = C2 ,
C3 = −C2 ,
por lo tanto, el vector pedido tendr´ la forma
a
→
−
C = C2 i + C2 j − C2 k.
Aplicando la condici´n 1), obtenemos
o
2 2 2 2
(C2 ) + (C2 ) + (−C2 ) = 3 (C2 ) = 1,
41

42. de donde,
1
C2 = ± ,
3
finalmente, el vector pedido tiene la forma
→
− 1
C = i+j−k .
3
42

43. Problema 24.
1
Demuestre que la l´
ınea recta x = y = 3 (z + 2) es paralela al plano 2x +
8y + 2z = 5.
Soluci´n:
o
La ecuaci´n de la recta dada se puede reescribir de la forma,
o
x−0 y−0 z − (−2)
= = ,
1 1 3
esta ecuaci´n, representa a una recta que pasa por el punto →0 = (0, 0, −2)
o −
r
→
−
y es paralela al vector A = (1, 1, 3). Por otro lado, de la ecuaci´n del plano,
o
→
−
tenemos que el vector N = (2, 8, 2) es un vector normal al plano, de esta forma
para mostrar que la recta y el plano son paralelos, debemos mostrar que el
→
− →
−
vector N , que es normal al plano y el vector A , que es paralelo a la recta son
→ →
− −
perpendiculares, es decir que satisfacen la condici´n N · A = 0.
o
→
− →
−
Calculando el producto escalar del vector normal N y el vector A , obten-
emos
→ →
− −
N · A = (2, −8, 2) · (1, 1, 3) = 0,
−
→
por lo tanto, se comprueba que el vector A es perpendicular al vector normal
→
− →
−
N del plano, y como el vector A es paralelo a la recta, luego entonces tambi´ne
es paralelo al plano y por lo tanto, la recta dada tambi´n es paralela al plano.
e
43

44. Problema 25.
Las ecuaciones param´tricas de una recta son:
e
x = 3t + 1,
y = −2t + 4,
z = t − 3,
encuentre la ecuaci´n del plano que contiene a dicha recta.
o
Soluci´n:
o
Las ecuaciones param´tricas de la recta dada son equivalentes a la ecuaci´n
e o
vectorial de la forma,
→(t) = (1, 4, −3) + t(3, −2, 1),
−
r
que por definici´n es la ecuaci´n de una recta en forma param´trica que pasa por
o o e
un punto cuyo vector de posici´n est´ dado por → = (1, 4, −3) y es paralela al
o a −
r0
−
→ − → →− −
vector A = (3, −2, 1). Si hacemos → × A = N que es un vector perpendicular al
r0
→
−
vector A y tambi´n perpendicular a →, entonces, la ecuacion del plano pedida
e −
r0
ser´ de la forma,
a
ax + by + cz = d,
donde
− → −
d = → · N,
r0
y
→
−
N = ai + bj + ck,
es decir,
→
− i j k
N = 1 4 −3 = −2i − 10j − 14k
3 −2 1
asimismo,
→ →
− −
d = N · r0
= (−2i − 10j − 14k) · (i + 4j − 3k)
= −2 − 40 + 42 = 0,
por lo tanto, la ecuaci´n del plano ser´ de la forma −2x − 10y − 14z = 0, que
o a
se puede escribir finalmente como,
x + 5y + 7z = 0.
44

45. Problema 26.
Determine las ecuaciones de la l´ınea recta (en forma param´trica y sim´trica)
e e
que pasa por el punto (3, 2, −4), paralela a la l´
ınea de intersecci´n de los planos
o
x + 3y − 2z = 8,
x − 3y + z = 0.
Soluci´n:
o
De las ecuaciones de los planos, los vectores
−
→
N1 = i + 3j − 2k,
−
→
N2 = i − 3j + k,
−→ − →
son vectores normales a cada plano respectivamente, de esta forma N1 × N2
−
→ −
→
resulta ser un vector que es perpendicular tanto a N1 como a N2 , por lo que
−→ → − −→ − →
el vector N1 × N 2 ser´ paralelo a ambos planos y por lo tanto N1 × N2 ser´
a a
paralelo a la l´
ınea de intersecci´n de ambos planos. Calculando el producto
o
vectorial de las normales,
→ −
− → − → i j k
A = N1 × N2 = 1 3 −2 = −3i − 3j − 6k,
1 −3 1
por lo tanto, la ecuaci´n de la recta en forma param´trica ser´ de la forma,
o e a
→(t) = → + t→
−
r −
r0
−
A
es decir,
→(t) = (3, 2, −4) + t(−3, −3, −6),
−
r
y para determinar la forma sim´trica de la recta, debemos eliminar el par´metro
e a
t de la ecuaci´n vectorial, para hacer esto, escribimos las componentes de esta
o
ecuaci´n vectorial de la forma,
o
x = 3 − 3t,
y = 2 − 3t,
z = −4 − 6t,
despejando el par´metro t e igualando obtenemos,
a
x−3 y−2 z+4
= =
−3 −3 −6
o tambi´n,
e
z+4
x−3=y−2= .
2
45

46. Problema 27.
Encontrar el punto de intersecci´n (si es que se intersectan) de las siguientes
o
l´
ıneas rectas.
→ (t) = 5i + 4j + 5k t + 7i + 6j + 8k,
−
r1
a).− → (t) = 6i + 4j + 6k t + 8i + 6j + 9k,
−
r2
→ (t) = 2k + 3i + 2j + k t,
−
r1
b).− → (t) = 3i + 2j + 3k + 6i + 4j + 2k t,
−
r2
Soluci´n:
o
a).− Las ecuaciones anteriores son de la forma,
→(t) = → + t→,
−
r −
r0
−
A
que representa la ecuaci´n param´trica de una recta L que pasa por el punto
o e
→
−
(x0 , y0 , z0 ) y es paralela al vector A . La ecuaci´n anterior es equivalente a las
o
ecuaciones
x = x0 + at,
y = y0 + bt,
z = z0 + ct,
que tambi´n se les llaman las ecuaciones param´tricas de la recta L, ´stas ecua-
e e e
ciones son equivalentes a las ecuaciones no param´tricas de la recta L dadas
e
por,
x − x0 y − y0 z − z0
= = .
a b c
De lo anterior, para las rectas dadas tenemos las siguientes ecuaciones param´tricas
e
para cada recta,
x = 7 + 5t, x = 8 + 6t,
y = 6 + 4t, y y = 6 + 4t,
z = 8 + 5t, z = 9 + 6t,
que son equivalentes a las siguientes ecuaciones no param´tricas respectiva-
e
46

47. mente,
x−7 y−6 z−8
= = ,
5 4 5
x−8 y−6 z−9
= = .
6 4 6
Las ecuaciones anteriores constituyen un conjunto de cuatro ecuaciones que
han de satisfacer las 3 inc´gnitas x, y y z, si consideramos las tres primeras
o
ecuaciones, obtenemos
x−7 y−6
1) 5 = 4 ,
y−6 z−8
2) 4 = 5 ,
x−8 y−6
3) 6 = 4 .
Resolviendo el sistema, de las ecuaciones 1) y 3), obtenemos
x−7 x−8
= ,
5 6
de donde obtenemos que x = 2, sustituyendo en la ecuaci´n 1),
o
2−7 y−6
= ,
5 4
de donde y = 2, finalmente de la ecuaci´n 2) obtenemos z = 3. N´tese que ´stos
o o e
valores tambi´n satisfacen la cuarta ecuaci´n y−6 = z−9 . Por lo tanto, el punto
e o 4 6
de intersecci´n de las dos rectas tiene al vector 2 i + 2j + 3k como vector de
o
posici´n.
o
b).− Como se indic´ anteriormente, las ecuaciones para →1 (t) y →2 (t) son
o −r −
r
de la forma r→(t) = → + t→, en este caso los vectores → = 3i + 2j + 3k y
− −
r0
−
A
−
A1
→
−
A 2 = 6i + 4j + 2k, son vectores paralelos a cada recta respectivamente, pero
→
− →
− →
− →
−
A 2 = 2 3i + 2j + k = 2 A 1 , es decir, A 1 A 2 , por lo que ambas l´ ıneas rectas
son paralelas que pasan por los puntos (0, 0, 2) y (3, 2, 3) y por lo tanto, nunca
se van a intersectar.
47

48. Problema 28.
Encontrar la ecuaci´n del plano que contiene a las siguientes l´
o ıneas rectas,
3−y x−2 2y+1
2+x= 2 =z y 2 = 2 =z−1
Soluci´n:
o
Por definici´n, la ecuaci´n de un plano es de la forma,
o o
ax + by + cz = d,
→ →
− −
donde d = →0 · N , r 0 es el vector de posici´n de un punto que este en el plano
−r o
→
−
y N = (a, b, c) es un vector normal o perpendicular al plano. De esta forma
para encontrar la ecuaci´n del plano necesitamos un punto en o sobre ´ste y un
o e
vector normal o perpendicular al mismo.
Las ecuaciones anteriores se pueden reescribir de la siguiente forma,
x − (−2) y−3 z−0
= = ,
1 −2 1
x−2 y − −1 2 z−1
= = ,
2 1 1
si comparamos estas ecuaciones con la ecuaci´n general de la recta x−x0 =
o a
→
−
y−y0
b = c , que son equivalentes a la ecuaci´n vectorial →(t) = → + t A ,que
z−z0
o −r −
r0
representa la ecuaci´n param´trica de una recta L que pasa por el punto (x 0 , y0 , z0 )
o e
→
−
y es paralela al vector A , las ecuaciones de las rectas dadas son equivalentes a
las ecuaciones,
→ (t) = → + t→ = (−2, 3, 0) + t (1, −2, 1) ,
−
r1 −
r 01
−
A
→ (t) = → + t→ = 2, − 1 , 1 + t (2, 1, 1) .
−r2 −r 02
−
B 2
De las ecuaciones anteriores, si hacemos el producto vectorial de los vectores
paralelos a cada recta, obtendremos un vector normal o perpendicular a cada
recta, y por lo tanto perpendicular al plano buscado que contiene a las dos
rectas, de esta forma calculando el producto vectorial,
→ → →
− − − i j k
N = A×B = 1 −2 1 = −3i + j + 3k,
2 1 1
→
−
por lo tanto, sustituyendo en la ecuaci´n general de un plano, el vector N y
o
cualquier punto que este sobre el plano, por ejemplo el punto (−2, 3, 0) por
donde pasa la primera recta, obtenemos
48

49. −3x + y + 3z = (−2, 3, 0) · (−3, 1, 3),
finalmente, la ecuaci´n del plano pedida est´ dada por,
o a
−3x + y + 3z = 9
49

50. Problema 29.
→
− →
−
Sean P = 3i + j + 2k y Q = i − 2j − 4k los vectores de posici´n de los o
puntos P y Q respectivamente.
a) Hallar la distancia d desde el punto (−1, 1, 1) a la recta que une los puntos
P y Q.
b) Hallar la ecuaci´n del plano que pasa por el punto P y es perpendicular
o
a la recta P Q.
c) Hallar la distancia D del punto (−1, 1, 1) al plano calculado en b).
Soluci´n:
o
a) Por definici´n, la distancia de un punto de coordenadas (x 1 , y1 , z1 ) a una
o
→
−
recta de la forma →(t) = →0 + t A , est´ dada por:
−r −r a
→
−
(→ 1 − → 0 ) × A
−
r −
r
d= →
−
A
donde →0 es el vector de posici´n del punto por donde pasa la recta L, →1 es
−r o −
r
el vector de posici´n del punto a donde se quiere calcular la distancia a la recta
o
→
−
L y el vector A es un vector que es paralelo a la recta L. Por lo tanto, para
calcular la distancia del punto (−1, 1, 1) a la recta que une los puntos P y Q,
→
−
escribamos dicha ecuaci´n de la recta en la forma →(t) = →0 + t A para as´
o −r −r ı
aplicar la ecuaci´n anterior.
o
→
−
Aplicando la ecuaci´n →(t) = →0 + t A , para los vectores de posici´n de
o − r −r o
los puntos P y Q, la ecuaci´n de la recta que une los puntos P y Q se puede
o
escribir vectorialmente de la forma,
→(t) = → + t → − →
−
r
−
P
− −
Q P
es decir,
→(t) = 3i + j + 2k + t
−
r i − 2 j − 4 k − 3i + j + 2 k
→(t) = 3i + j + 2k + t −2i − 3j − 6k
−
r
por lo tanto, en la ecuaci´n anterior tenemos que,
o
→
−
r0 = (3, 1, 2)
→
−
A = (−2, −3, −6)
adem´s,
a
→ = (−1, 1, 1)
−
r1
50

51. aplicando la ecuaci´n para la distancia de un punto a una recta obtenemos,
o
|[(−1, 1, 1) − (3, 1, 2)] × (−2, −3, −6)|
d =
|(−2, −3, −6)|
|(−4, 0, −1) × (−2, −3, −6)|
= √
4 + 9 + 36
calculando el producto vectorial,
i j k
(−4, 0, −1) × (−2, −3, −6) = −4 0 −1 = −3i − 22j + 12k
−2 −3 −6
Finalmente, la distancia del punto (−1, 1, 1) a la recta que une los puntos P
y Q est´ dada por:
a
−3i − 22j + 12k √ √
9 + 484 + 144 637
d= √ = =
49 7 7
b) Por definici´n la ecuaci´n
o o
→
−
(→ − →0 ) · N = 0,
− −
r r
representa la ecuaci´n de un plano que contiene a un punto de coordenadas
o
→
−
(x0 , y0 , z0 ) y un vector normal N = ai + bj + ck. En este, caso la ecuaci´n
o
del plano que pasa por el punto P y es perpendicular a la recta P Q se puede
escribir vectorialmente de la forma,
→−→ · →−→ =0
− −
r P
− −
Q P
→ →
− −
donde Q − P es un vector que es paralelo a la recta y que es perpendicular al
→ →
− −
plano buscado, sustituyendo los valores para los vectores P y Q , obtenemos
(x − 3, y − 1, z − 2) · (−2, −3, −6) = 0
calculando el producto escalar se obtiene,
2x + 3y + 6z = 21
que es la ecuaci´n del plano que contiene al punto de coordenadas (3, 1, 2) y es
o
perpendicular a la recta P Q.
51

52. c) Por definici´n, la ecuaci´n que proporciona la distancia de un punto de
o o
coordenadas (x1 , y1 , z1 ) al plano ax + by + cz = d est´ dada por:
a
|ax1 + by1 + cz1 − d|
D= √ ,
a2 + b 2 + c 2
→ −
−
donde d = N · →0 = ax0 + by0 + cz0 .
r
Aplicando la ecuaci´n anterior, y la ecuaci´n para el plano calculada en el
o o
inciso b) obtenemos,
|2(−1) + 3(1) + 6(1) − 21| |7 − 21|
D= √ = √ =2
2 2 + 32 + 62 49
que es la distancia del punto (−1, 1, 1) al plano 2x + 3y + 6z = 21.
52

53. Problema 30.
|
Calcule la distancia entre los planos
x + 2y + 3z = 5,
x + 2y + 3z = 19.
Soluci´n:
o
Para encontar la distancia entre los planos, tomemos un punto arbitrario
en el primer plano (observe que los planos dados son paralelos), por ejemplo el
punto (0, 1, 1) y apliquemos la expresi´n para calcular la distancia de un punto
o
de coordenadas (x1 , y1 , z1 ) al plano ax + by + cz = d, dada por la expresi´n:
o
|ax1 + by1 + z1 − d|
D= ,
(a2 + b2 + c2 )
→ −
−
donde a, b y c, son las componentes del vector normal al plano y d = N · →0 ,
r
siendo →0 el vector de posici´n de un punto sobre el plano. En este caso,
−
r o
tenemos
→
−
N = (a, b, c) = (1, 2, 3),
→
−
r1 = (x1 , y1 , z1 ) = (0, 1, 1),
y
d = 19,
sustituyendo los valores anteriores en la expresi´n para la distancia, obtenemos
o
|1(0) + 2(1) + 3(1) − 19|
D = √
12 + 22 + 32
|2 + 3 − 19| |−14|
= √ = √
14 14
14 √
= √ = 14.
14
Obs´rvese que como los planos son paralelos, el problema tambi´n se puede
e e
resolver al considerar cualquier punto en el segundo plano y en ese caso d = 5.
53

54. 3 Problemas del cap´
ıtulo 2.
Problema 1.
Escribir las ecuaciones param´tricas y no param´tricas, de los siguientes
e e
c´
ırculos:
a) centro en (0, 1, 0), radio √ paralelo al plano XZ,
2,
b) centro en (1, 1, 1), radio 3, paralelo al plano XY,
c) centro en (−1, 2, 3), radio 9, paralelo al plano XZ,
d) centro en (−1, 3, −1), radio 5, paralelo al plano Y Z.
Soluci´n.
o
Por definici´n, la ecuaci´n
o o
→
− →
−
(∗) R (θ) = R 0 + (a cos θ) e1 + (a sin θ) e2 ,
representa un c´ırculo con centro en el punto (x 0 , y0 , z0 ) y paralelo al plano
formado por los vectores unitarios e1 y e2 que son mutuamente perpendiculares,
donde θ est´ entre 0 y 2π.
a
a) Aplicando la ecuaci´n anterior en este caso,
o
a = 2
e1 = i
e2 = k
→
−
R0 = (0, 1, 0),
por lo tanto, la ecuaci´n pedida es
o
→
−
R (θ) = (0, 1, 0) + (2 cos θ) i + (2 sin θ) k
o bien,
→
−
R (θ) = 2 cos θ i + j + 2 sin θ k
es decir, las ecuaciones param´tricas de un c´
e ırculo de radio 2 paralelo al plano
XZ con centro en (0, 1, 0) son:
x = 2 cos θ,
y = 1,
z = 2 sin θ,
que son equivalentes a las ecuaciones no param´tricas,
e
x2 + z 2 = 4,
y = 1.
54

55. b) En este caso tenemos, aplicando la ecuaci´n (∗) obtenemos,
o
√
a = 3
e1 = i
e2 = j
→
−
R0 = (1, 1, 1),
por lo tanto, la ecuaci´n pedida es
o
→
− √ √
R (θ) = (1, 1, 1) + 3 cos θ i + 3 sin θ j,
o bien,
→
− √ √
R (θ) = 1 + 3 cos θ i + 1 + 3 sin θ j + k,
que es equivalente a las siguientes ecuaciones param´tricas:
e
√
x = 1 + 3 cos θ,
√
y = 1 + 3 sin θ,
z = 1,
de donde obtenemos las ecuaciones no param´tricas, de la forma
e
(x − 1)2 + (y − 1)2 = 3,
z = 1.
c) An´logamente, de la ecuaci´n (∗) obtenemos
a o
a = 9
e1 = i
e2 = k
→
−
R0 = (1, 2, 3),
por lo tanto, la ecuaci´n del c´
o ıculo en forma param´trica est´ dada por,
e a
→
−
R (θ) = (1 + 9 cos θ) i + 2j + (3 + 9 sin θ) k,
que es equivalente a las siguientes ecuaciones param´trica:
e
x = 1 + 9 cos θ,
y = 2,
z = 3 + 9 sin θ,
55

56. de donde obtenemos las ecuaciones no param´tricas, de la forma
e
(x − 1)2 + (z − 3)2 = 81,
y = 2.
d) De un procedimiento similar a los incisos anteriores se obtiene,
→
−
R (θ) = −i + (3 + 5 sin θ) j + (−1 + 5 sin θ) k,
y
(y − 3)2 + (z + 1)2 = 25,
x = −1..
56

57. Problema 2.
Dada la curva
→
− t2 t3
R = 2i + 3 k; 0 t 2,
encontrar un vector unitario T (s),donde s es la longitud de arco.
Soluci´n.
o
Para encontrar T (s), primero debemos reparametrizar la curva en t´rminos
e
→
−
de la longitud de arco s, es decir; obtener R (s) para as´ calcular:
ı
→
−
d R (s)
T (s) = ,
ds
sabemos que la longitud de arco est´ dada por la expresi´n:
a o
t −
→
s(t) = R (t) dt,
0
de la ecuaci´n de la curva obtenemos,
o
→
−
R (t) = ti + t2 k;
de donde,
−
→
R (t) = t2 + t 4 = t (1 + t2 ),
sustituyendo en la expresi´n para la longitud de arco,
o
t
s(t) = t (1 + t2 )dt.
0
Para resolver la integral, hacemos un simple cambio de variable de la forma
u = 1 + t2 ,
du = 2tdt,
du
dt = ,
2t
de esta forma,
t t
1 du 1 1
s(t) = tu 2 = u 2 du
0 2t 2 0
3 t
2
(1 + t ) 2 1 3
= = (1 + t2 ) 2 − 1 ,
3 3
0
por lo tanto, la longitud de arco de la curva est´ dada por,
a
57

58. 1 3
(1 + t2 ) 2 − 1
s(t) =
3
de esta expresi´n, despejamos el par´metro t de la forma;
o a
2
(3s + 1) 3 = 1 + t2 ;
1
2 2
t(s) = (3s + 1) 3 − 1 ,
→
−
sustituyendo en la expresi´n para R (t(s)), obtenemos
o
3
→
− 1 2 1 2 2
R (s) = (3s + 1) 3 − 1 i + (3s + 1) 3 − 1 k,
2 3
derivando esta expresi´n con respecto al par´metro s,
o a
1
1 2 −1 1 2 2 2 2 1
T (s) = (3s + 1) 3 (3) i+ (3s + 1) 3 − 1 (3s + 1)− 3 (3) k,
2 3 3 3 3
finalmente, el vector unitario est´ dado por:
a
1
1 1 2 2
T (s) = 1 i+ 1 (3s + 1) 3 − 1 k.
(3s + 1) 3 (3s + 1) 3
Observemos que inmediatamente se puede verificar que T (s) = 1, aplicando
la definici´n de la magnitud de un vector tenemos,
o
1 1 2
T (s) = 2 + 2 (3s + 1) 3 − 1
(3s + 1) 3 (3s + 1) 3
1 2
= 2 1 + (3s + 1) 3 − 1
(3s + 1) 3
2
(3s + 1) 3
= 2
(3s + 1) 3
= 1
58

59. Problema 3:
Dada la curva cuyas ecuaciones param´tricas son:
e
t
x = ,
2π
y = sin t,
z = cos t,
calcular la longitud de arco entre el punto (0, 0, 1) y el punto (1, 0, 1) . ¿Cu´l es
a
el vector unitario tangente a la curva dada en el punto (0, 0, 1)?.
Soluci´n:
o
De las ecuaciones param´tricas, la curva est´ dada por la ecuaci´n
e a o
→ (t) = t i + sin tj + cos tk,
−
r
2π
donde 0 ≤ t ≤ 2π. Por definici´n la longitud de una curva en el espacio desde
o
el punto en t = a, al punto en t = b, est´ dada por:
a
t=b
d→ (t)
−
r
l(t) = dt,
t=a dt
de la ecuaci´n de la curva dada, obtenemos
o
d→ (t)
−
r 1
= i + cos tj − sin tk,
dt 2π
de donde,
d→ (t)
−
r 1 1 + 4π 2
= + cos2 + sin2 t = ,
dt 4π 2 4π 2
sustituyendo en la expresi´n para calcular la longitud de la curva obtenemos,
o
59

60. 2π
√ √ t=2π
1 + 4π 2 1 + 4π 2
l= dt = t = 1 + 4π 2 .
0 2π 2π
t=0
As´ mismo por definici´n, el vector tangente a una curva en cualquier punto
ı o
del espacio est´ dado por:
a
d→(t)
−
r
dt
T (t) = ,
d→(t)
−
r
dt
en el punto (0, 0, 1) , es decir, en t = 0, obtenemos
d→ (t = 0)
−
r 1
= i + j,
dt 2π
y
√
d→ (t = 0)
−
r 1 + 4π 2
= ,
dt 2π
por lo tanto el vector unitario pedido est´ dado por:
a
i + 2π j
T =√ .
1 + 4π 2
60

61. Problema 4:
Si T denota la tangente unitaria a la curva,
x = t,
y = 2t + 5,
z = 3t,
demuestre que
dT
= 0,
dt
interprete este resultado en forma geom´trica.
e
Soluci´n:
o
En este caso, sustituyendo las ecuaciones param´tricas, la curva est´ dada
e a
por la ecuaci´n
o
→ (t) = ti + (2t + 5) j + 3tk.
−
r
En forma an´loga al problema anterior, el vector tangente a una curva en
a
cualquier punto del espacio est´ dado por:
a
d→(t)
−
r
dt
T (t) = ,
d→(t)
−
r
dt
de esta forma, de la ecuaci´n de la curva obtenemos,
o
i + 2j + 3k i + 2j + 3k
T =√ = √
1 2+4+9 14
de donde obtenemos,
dT
= 0.
dt
61

62. Por otro lado, obs´rvese que las ecuaciones param´tricas de la curva dada
e e
son equivalentes a la ecuaci´n,
o
x−0 y−5 z−0
= = ,
1 2 3
que es la ecuaci´n de una l´
o ınea recta que pasa por el punto de coordenadas
→
−
(0, 5, 0) y es paralela al vector A = i+2j+3k, como se ilustra esquem´ticamente
a
en la siguiente figura.
ftbpF260.9375pt294.5pt0ptFigure
b
Por lo tanto, la expresi´n dT = 0 indica que el vector T es constante a lo
o dt
largo de la l´
ınea recta, por lo que la direcci´n de la curva debe estar dada por
o
→
−
un vector unitario en la direcci´n del vector A , como era de esperarse.
o
62

63. Problema 5:
a) Determine la longitud de arco de la curva dada por las siguientes ecua-
ciones param´tricas,
e
x = et cos t,
y = et sin t,
z = 0,
entre t = 0 y t = 1.
b) Reparametrizar la curva en t´rminos de la longitud de arco.
e
Soluci´n:
o
a) De las ecuaciones param´tricas, la curva est´ dada por la ecuaci´n
e a o
→ (t) = et cos ti + et sin tj,
−
r
donde 0 ≤ t ≤ 1. Por definici´n la longitud de una curva en el espacio desde el
o
punto en t = a, al punto en t = b, est´ dada por:
a
t=b
d→ (t)
−
r
l(t) = dt,
t=a dt
de la ecuaci´n de la curva dada, obtenemos
o
d→ (t)
−
r
= −et (sin t) + et cos t i + et cos t + et sent j,
dt
de donde,
d→ (t)
−
r 2 2
= [et (− sin t + cos t)] + [et (cos t + sin t)]
dt
= e2t sin2 t + cos2 t − 2 sin t cos t + e2t cos2 t + sin2 t + 2 sin t cos t
√
= 2e2t
√ t
= 2e ,
63

64. sustituyendo en la expresi´n para calcular la longitud de la curva obtenemos,
o
√ 1 √ 1 √
l= 2 et dt = 2 et 0
= 2 [e − 1] .
0
b) Para reparametrizar la curva en t´rminos de la longitud de arco s, tenemos
e
por definici´n, que la longitud de arco s (t) est´ dada por la expresi´n,
o a o
t
d→ (t)
−
r
s = s(t) = dt,
t=t1 dt
para t ≥ t1 , en este caso escogemos t1 = 0. Por lo tanto la longitud de arco est´
a
dada por:
√ t
s (t) = 2 et dt
0
√
= 2 et − 1 ,
de la expresi´n anterior despejamos a t en funci´n de la longitud de arco s,
o o
de la forma
1
et = √ s + 1,
2
es decir,
√
s s+ 2
t(s) = log √ +1 = log √ ,
2 2
por lo tanto, la ecuaci´n de la curva en t´rminos de la longitud de arco s est´
o e a
dada por:
√ √ √
→ (t(s)) = exp log
− s+ 2 s+ 2 s+ 2
r √ cos log √ i + sin log √ j ,
2 2 2
64

65. finalmente obtenemos,
√ √ √
→(s) = s + 2 cos log
−
r √
s+ 2
√ i + sin log
s+ 2
√ j .
2 2 2
65

66. Problema 6:
Para la curva dada por las ecuaciones param´tricas,
e
x = sin t − t cos t,
y = cos t + t sin t,
z = t2 ,
encontrar,
a) La longitud de arco entre el punto (0, 1, 0) y el punto −2π, 1, 4π 2
b) T (t) .
c) T (π) .
Soluci´n:
o
En forma an´loga a los problemas anteriores, en este caso la longitud de la
a
curva estar´ dada por:
a
2π
d→ (t)
−
r
l= dt
0 dt
en este caso,
d→ (t)
−
r
= (cos t − cos t + t sin t) i + (− sin t + sin t + t cos t) j + 2tk
dt
= t sin ti + t cos tj + 2tk
por lo tanto,
2π
l = t2 sin2 t + t2 cos2 t + 4t2 dt
0
√ 2π
2π √ 5 2
= 5t2 dt = t
0 2
0
√
5 2
= 4π ,
2
finalmente la longitud de la curva desde el punto (0, 1, 0) al punto −2π, 1, 4π 2 ,
est´ dada por
a
√
l = 2 5π 2 .
66

67. b) En forma an´loga a los problemas anteriores, en este caso, el vector
a
tangente a la curva en cualquier punto del espacio est´ dado por:
a
→ (t)
−
r
T (t) = → (t)|
−
|r
t sin ti + cos tj + 2tk
=
t2 sin2 t + t2 cos2 t + 4t2
t sin ti + t cos tj + 2tk
= √ ,
t 5
finalmente,
1
T (t) = √ sin ti + cos tj + 2k .
5
c) As´ mismo en el punto t = π, el vector tangente est´ dado por:
ı a
1
T (t = π) = √ −j + 2k .
5
67

68. Problema 7.
a) Sea el campo escalar φ dado por:
1
φ(x, y, z) =
x2 + y 2 + z 2
Calcular el gradiente de φ en el punto (1, 0, −1).
Soluci´n.
o
Aplicando la definici´n del gradiente, obtenemos
o
∂ 1 ∂ 1 ∂ 1
φ = , ,
∂x x2 + y2 + z2 ∂y x2 + y2 + z2 ∂z x2 + y2 + z2
1 1
= − 3 2xi + 2y j + 2z k
2 (x2 + y2 + z2 ) 2
xi + y j + z k
= − 3
(x2 + y 2 + z 2 ) 2
por lo tanto en el punto (1, 0, −1), el gradiente de φ est´ dado por:
a
1
φ(1, 0, −1) = − 3 (i − k)
(1 + 0 + 1) 2
es decir,
1
φ(1, 0, −1) = √ (−i + k).
2 2
b) Dado el campo vectorial
−
→ xi + y j + z k
f (x, y, z) =
x2 + y 2 + z 2
calcular
→
−
i) · f en (1, −2, 1).
→
−
j) × f en (1, −2, 1).
Soluci´n.
o
i) El campo vectorial es de la forma:
→
− x y z
f (x, y, z) = i+ i+ i
x2 + y 2 + z 2 x2 + y 2 + z 2 x2 + y 2 + z 2
Aplicando la definici´n de la divergencia, se tiene
o
68

69. ∂f1 ∂ x
=
∂x ∂x x2 + y2 + z2
1 1
1 −2
x2 + y 2 + z 2 2
−x 2 x2 + y 2 + z 2 2x
=
(x2 + y2 + z2)
1
2 −2
x2 + y 2 + z x2 + y 2 + z 2 − x 2
=
(x2 + y 2 + z 2 )
finalmente,
∂f1 y2 + z2
= 3
∂x (x2 + y 2 + z 2 ) 2
de forma an´loga obtenemos,
a
∂f2 ∂ y x2 + z 2
= = 3
∂y ∂y x2 + y 2 + z 2 (x2 + y 2 + z 2 ) 2
y
∂f3 ∂ z x2 + y 2
= = 3
∂z ∂z x2 + y 2 + z 2 (x2 + y 2 + z 2 ) 2
por lo tanto la difvergencia de la funci´n vectorial dada resulta,
o
→
− 1
· f = 3 (y 2 + z 2 + x2 + z 2 + x2 + y 2 )
(x2+ y2 + z2 ) 2
2(x2 + y 2 + z 2 ) 2
= 3 =
(x2 + y2 + z2) 2 (x2 + y 2 + z 2 )
por lo tanto, la divergencia del campo vectorial evaluado en el punto (1, −2, 1)
resulta
→
− 2 2
· f (1, −2, 1) = =
(12 + (−2)2 + 12 ) 3
Soluci´n alternativa.
o
→
−
a) El campo vectorial f (x, y, z) se puede representar de la siguiente forma:
→
− →
−
f (x, y, z) = φ(x, y, z) A (x, y, z)
donde:
69

70. 1
φ(x, y, z) =
x2 + y2 + z2
→
− →.
−
A (x, y, z) = r
Si aplicamos la siguiente propiedad del operador vectorial nabla obtenemos
1) · (φ→) =
−
r φ·→+φ
−
r · →,
−
r
pero del inciso a) se obtuvo que,
1 xi + y j + z k
=− 3
x2 + y2 + z2 (x2 + y 2 + z 2 ) 2
que se puede escribir como
→
−
φ = − rr3 ,
(2)
donde r es la magnitud del vector de posici´n →.
o − r
Por otro lado de la definici´n de la divergencia se tiene,
o
(3) ·→=
−
r ∂x
∂x + ∂y
∂y + ∂z
∂z = 3,
sustituyendo las ecuaciones (2) y (3) en la ecuaci´n (1) obtenemos,
o
→
−
r → 3
· (φ→) =
−
r − ·− +
r
r3 r
2
=
r
que es el mismo resultado que se obtuvo anteriormente.
En general si un campo escalar φ(x, y, z) se puede representar de la forma,
φ(x, y, z) → φ(r)
donde r es la magnitud del vector de posici´n, entonces
o
∂φ
φ(r) = e→
−
∂r r
→
−
donde r = |→| = x2 + y 2 + z 2 y er =
−
r r
r .
Por ejemplo, si
1
φ(x, y, z) = ln 3
(x2 + y2 + z2 ) 2
que se puede escribir como
1
φ(r) = ln = −3 ln r
r3
70

71. de donde,
∂φ 3
=−
∂r r
y por lo tanto,
∂φ 3 →
−
r 3→
φ(r) = er = − =− −.
r
∂r r r r2
Por otro lado, si aplicamos la definici´n del gradiente, tenemos
o
3 1
φ(x, y, z) = 2xi + 2y j + 2z k
2 x2 + y 2 + z 2
es decir,
3 3→ −.
φ(x, y, z) = xi + y j + z k = r
x2 + y2 + z2 r2
j) Si el campo vectorial esta dado como
→
− xi + y j + z k
f (x, y, z) =
x2 + y 2 + z 2
Por definici´n del rotacional tenemos,
o
i j k
→
− ∂ ∂ ∂
× f = ∂x ∂y ∂z
√ 2 x2 2 √ 2 y2 2 √ 2 z2 2
x +y +z x +y +z x +y +z
calculando las derivadas parciales, obtenemos
→
− yz yz
× f = − 3 + 3 i
(x2 + y 2 + z 2 ) 2
(x2 + y 2 + z 2 ) 2
xz xz
− − 3 + 3 i
(x2 + y2 + z2) 2 (x2 + y2 + z2 ) 2
xy xy
+ − 3 + 3 i
(x2 + y 2 + z 2 ) 2
(x2 + y 2 + z 2 ) 2
es decir,
→ →
− −
× f = 0
Soluci´n alternativa.
o
De la misma forma que en el inciso i) si aplicamos la propiedad del operador
→
− →
− →
−
”NABLA” × φ(r) A = φ(r) × A + φ(r) × A , identificando a φ(r) = 1 r
→ −
−
y A = → tenemos,
r
71

72. →
−
(4) × r
r = 1
r ×→+
−
r 1
r × →,
−
r
adem´s, de la definici´n del rotacional tenemos que,
a o
i j k
→
−
(5) ×→=
−
r ∂
∂x
∂
∂y
∂
∂z
= 0,
x y z
y del inciso a), obtenemos
1 →
−
(6) r = − rr3 ,
sustituyendo las ecuaciones (5) y (6) en la ecuaci´n (4), obtenemos
o
→
−
r →
−
r
× = − × →,
−
r
r r3
aplicando la definici´n del producto vectorial de dos vectores
o
→ × → = →,
− −
r r
−
0
finalmente obtenemos,
→
−
r →
−
× = 0,
r
que es el mismo resultado que se obtuvo aplicando la definici´n del determinante
o
para el rotacional.
72

73. Problema 8.
El potencial electrost´tico V debido a dos filamentos paralelos infinitos de
a
densidades lineales λ y −λ est´ dado por,
a
∂ r2
V = ln( ),
2πε0 r1
donde
2
r1 = (x − x0 )2 + y 2 ,
y
2
r2 = (x + x0 )2 + y 2 ,
consideremos los filamentos en la direcci´n z, pasando por el plano XY en
o
(−x0 , 0, 0) y (x0 , 0, 0). Verificar que:
λ x + x0 x − x0 1 1
V (x, y) = 2 − 2 i + 2y 2 − r2 j
2πε0 r1 r2 r1 2
Soluci´n:
o
2 2
Sustituyendo los valores de r1 y r2 , y aplicando la propiedad de los logar-
itmos, obtenemos
1
λ (x + x0 )2 + y 2 2
λ (x + x0 )2 + y 2
V (x, y) = ln = ln .
2πε0 (x − x0 )2 + y 2 4πε0 (x − x0 )2 + y 2
Por definici´n, sabemos que
o
∂V ∂V
V (x, y) ≡ i+ j.
∂x ∂y
Calculemos primeramente la derivada con respecto a x,
∂V (x, y) ∂ (x + x0 )2 + y 2
=k ln ,
∂x ∂x (x − x0 )2 + y 2
donde
λ
k= ,
2πε0
73

74. de esta forma,
∂V (x, y) (x − x0 )2 + y 2 (x − x0 )2 + y 2 2(x + x0 ) − (x + x0 )2 + y 2 2(x − x0 )
=k 2 ,
∂x (x + x0 )2 + y 2 [(x − x0 )2 + y 2 ]
sustituyendo
r1 = (x − x0 )2 + y 2 ,
2
y
2
r2 = (x + x0 )2 + y 2 ,
obtenemos,
2 2 2
∂V (x, y) r1 2(x + x0 )r1 − 2(x − x0 )r2
= k 2 4
∂x r2 r1
2 2
λ 2(x + x0 )r1 − 2(x − x0 )r2
= 2 r2
4πε0 r1 2
λ (x + x0 ) (x − x0 )
= 2 − 2 .
2πε0 r2 r1
An´logamente, para la derivada con respecto a y obtenemos,
a
∂V (x, y) ∂ (x + x0 )2 + y 2
= k ln
∂y ∂y (x − x0 )2 + y 2
(x − x0 )2 + y 2 (x − x0 )2 + y 2 − 2y (x + x0 )2 + y 2 2y
= k 2
(x + x0 )2 + y 2 [(x − x0 )2 + y 2 ]
2 2 2
r1 2y(r1 − r2
= k 2 4
r2 r1
1 1
= k2y 2 − 2 j.
r2 r1
Finalmente, sumando las derivadas parciales con respecto a x y a y obten-
emos,
λ x + x0 x − x0 1 1
V (x, y) = 2 − 2 i + 2y 2 − r2 j .
2πε0 r1 r2 r1 2
74

75. Problema 9.
Hallar:
a) La derivada direccional de φ(x, y, z) = x2 + y 2 + z 2 en la direcci´n del
o
punto P (1, 1, 0) al punto Q(2, 1, 1) y
b) Su valor m´ximo y direcci´n en el punto (1, 1, 0).
a o
Soluci´n:
o
a) Sean →P y →Q los vectores de posici´n de los puntos P y Q respectiva-
−r −
r o
mente, es decir
→
−
rP = i+j
→
−
r = 2i + j + k
Q
por lo tanto,
→ −→
−
rQ −P
r 2i + j + k − i + j 1
u= →− −→ |
− = = √ i+k
|rQ rP (2 − 1) 2 + (1 − 1)2 2
asimismo, de la definici´n del gradiente dada por la ecuaci´n,
o o φ(x, y, z) ≡
∂V ∂V ∂V
∂x i + ∂y j + ∂z k obtenemos,
φ = 2xi + 2y j + 2z k
sustituyendo en la expresi´n para la derivada direccional,
o
dφ
= φ·u
ds
1
= 2xi + 2y j + 2z k · √ i + k
2
2
= √ (x + z)
2
evaluando en el punto (1, 1, 0) finalmente obtenemos,
dφ(1, 1, 0) √
= 2.
ds
√
Es decir, el campo escalar se incrementa a una raz´n de 2 por unidad de
o
distancia cuando se avanza del punto P (1, 1, 0) al punto Q(2, 1, 1).
b) Por definici´n aplicando la propiedad del gradiente que establece, el valor
o
m´ximo de dφ ser´ igual a la magnitud del gradiente de φ, es decir;
a ds a
dφ √
= | φ| = 2 2
ds max
75

76. y tambi´n de la propiedad del gradiente, el valor m´ximo de dφ se tendr´ en
e a ds a
la direcci´n del gradiente φ(1, 1, 0) = 2(1) i + 2(1)j + 2(0)k, es decir, en la
o
direcci´n del vector 2i + 2j.
o
76

77. Problema 10.
Hallar la derivada de P = 4 exp (2x − y + z) en el punto (1, 1, −1) en di-
recci´n del vector (−3, 5, 6).
o
Soluci´n:
o
Por definici´n la derivada direccional est´ dada por:
o a
∂φ
= φ · u,
∂s
en este caso, la derivada direccional estar´ dada por,
a
∂P
= P · u,
∂s
calculando el gradiente de la funci´n P,
o
∂ ∂ ∂
P = (4 exp (2x − y + z)) i + (4 exp (2x − y + z)) i + (4 exp (2x − y + z)) i
∂x ∂x ∂x
= exp (2x − y + z) 8i − 4j + 4k ,
la direcci´n est´ dada en este caso por el vector,
o a
→
−
u −3i + 5j + 6k
u= → =
−| √ ,
|u 70
por lo tanto la derivada de la funci´n P en el punto (1, 1, −1) est´ dada por:
o a
∂P (1, 1, −1)
= P (1, 1, −1) · u
∂s
−3i + 5j + 6k
= exp (2(1) − (1) + (−1)) 8i − 4j + 4k · √
70
−24 − 20 + 24
= √
70
20
= −√ .
70
77

78. Problema 11
Calcule la derivada direccional de f (x, y, z) = x yz en el punto (e, e, 0) y en
la direcci´n del punto (1, 2, 3) hacia el punto (0, 3, 2).
o
Soluci´n:
o
Para calcular la derivada direccional de f (x, y, z), tenemos por definici´n que
o
df
= f · u,
ds
donde, f es el gradiente de la funci´n dada y u es el vector que indica la
o
direcci´n, que en este caso, est´ dada por el vector,
o a
→ = → − → = (0, 3, 2) − (1, 2, 3) = (−1, 1, −1),
−
u − −
r2 r1
de esta forma,
→
−
u 1
u = → = √ (−1, 1, 1).
−|
|u 3
Aplicando la definici´n del gradiente, obtenemos
o
∂ yz ∂ yz ∂ yz
f = [x ] i + [x ] j + [x ] k
∂x ∂y ∂z
∂ yz ∂ yz ∂ yz
= eln x i + eln x j + eln x k
∂x ∂y ∂z
yz ∂ yz ∂ yz ∂
= eln x (ln xyz ) i + eln x (ln xyz ) j + eln x (ln xyz ) k
∂x ∂y ∂y
yz 1 1 1
= eln x yzxyz−1 i + yz (z ln x) j + yz (y ln x) k ,
xyz x x
que se puede escribir de la forma,
f = yzxyz−1 i + z ln xj + y ln xk,
de esta forma en el punto (e, e, o), el gradiente est´ dado por:
a
f (e, e, o) = 0i + 0j + e ln(e)k
= e(0, 0, 1),
Finalmente la derivada direccional est´ dada por:
a
78

79. df 1
= e(0, 0, 1) · √ (−1, 1, 1)
ds 3
e
= √ .
3
79

80. Problema 12.
Encontrar los valores de las constantes a, b y c de forma que la derivada de
la funci´n
o
φ(x, y, z) = axy 2 + byz + cx3 z 2
en el punto (1, 2, −1) tenga un m´ximo de magnitud 64 en la direcci´n
a o
paralela al eje Z.
Soluci´n:
o
Por definici´n, la derivada direccional est´ dada por:
o a
dφ
= φ·u
ds
Aplicando las hip´tesis del problema, ´sta derivada ser´ m´xima en direcci´n
o e a a o
paralela al eje Z, es decir en direcci´n del vector k por lo tanto,
o
(1) φ · k = 64,
(2) φ · j = 0,
(3) φ · i = 0,
aplicando la definic´n del gradiente obtenemos,
o
φ = ay 2 + 3cx2 z 2 i + (2axy + bz)j + by + 2cx3 z k
evaluando en el punto (1, 2, −1), obtenemos
φ(1, 2, −1) = (4a + 3c) i + (4a − b)j + (2b − 2c) k
por lo tanto, de las ecuaciones (1), (2) y (3) obtenemos
(1a) 2b − 2c = 64,
(2a) 4a + 3c = 0,
(3a) 4a − b = 0,
de las ecuaciones (2a) y (3a) obtenemos,
b = −3c
al sustituir en la ecuaci´n (1a) obtenemos,
o
c = −8
nuevamente empleando las ecuaciones (21) y (3a) obtenemos,
80

81. a = 6
b = 24
81

82. Problema 13.
Dado el campo escalar,
φ(x, y, z) = 2xz + ey z 2
a) Encontrar dφ en el punto (2, 1, 1) y en la direcci´n del vector 2 i + 3j − k.
ds o
b) Cu´l es la direcci´n del m´ximo cambio de φ(x, y, z) en el punto (2, 1, 1)
a o a
y que valor tiene ´ste m´ximo cambio.
e a
c) Encuentre la ecuaci´n del plano tangente a φ(x, y, z) = 4 + e en el punto
o
(2, 1, 1).
Problema:
Por definici´n, sabemos que la derivada direccional est´ dada por:
o a
df
= f · u,
ds
donde, f es el gradiente de la funci´n dada y u es el vector que indica la
o
direcci´n, que en este caso, est´ dada por el vector,
o a
1
u = √ (2, 3, −1) ,
14
as´ mismo,
ı
∂φ ∂φ ∂φ
φ≡ i+ j+ k = 2z i + ey z 2 j + (2x + ey z) k,
∂x ∂y ∂z
de tal forma que en el punto (2, 1, 1) , el gradiente est´ dado por:
a
φ = 2i + ej + (4 + 2e)k
Por lo tanto, la derivada direccional est´ dada por:
a
df 1
= 2i + ej + (4 + 2e)k ·√ (2, 3, −1)
ds 14
1 e
= √ [4 + 3e − 4 − 2e] = √ .
14 14
b) La direcci´n en el cual el campo escalar φ est´ cambiando m´s r´pido,
o a a a
est´ dada en la direcci´n gradiente, de esta forma en el punto (2, 1, 1), tenemos
a o
φ(2, 1, 1) = 2i + ej + (4 + 2e)k,
y su m´ximo valor est´ dada por:
a a
| φ(2, 1, 1)| = 22 + e2 + (4 + 2e)2
= 20 + 16e + 5e2 .
82

83. c) El vector normal a la superficie en el punto (2, 1, 1) est´ dado por el
a
gradiente,
φ(2, 1, 1) = 2i + ej + (4 + 2e)j,
De esta forma, la ecuaci´n del plano tangente a φ(2, 1, 1) = 4 + e, est´ dada por
o a
φ • (→ − →) = 0,
− −
r r0
es decir,
2(x − 2) + e(y − 1) + (4 + 2e)(z − 1) = 0,
que tambi´n se puede escribir de la forma,
e
2x + ey + 4z = 8 + 3e.
83

84. Problema 14.
La temperatura de los puntos en el espacio est´ dada por:
a
T (x, y, z) = x2 + y 2 − z
a) Si un mosquito situado en el punto (1, 1, 2) se est´ muriendo de fr´ ¿En
a ıo.
qu´ direcci´n deber´ volar para que no se muera?
e o a
b) Si el mosquito vuela a una raz´n de 5 unidades de distancia por segundo en
o
direcci´n del vector 4i+4j−2k.
o
¿Cu´l es la raz´n de cambio de aumento en la temperatura por unidad de
a o
tiempo en el momento en que pasa el mosquito por el punto (1, 1, 2)?.
Soluci´n:
o
a) Como el gradiente de T a punta en la m´xima raz´n de cambio de la
a o
temperatura y el mosquito en el punto (1, 1, 2) se est´ muriendo de fr´ deber´
a ıo, a
moverse en la direcci´n del gradiente para calentarse.
o
Aplicando la definici´n del gradiente,
o
∂T ∂T ∂T
T (x, y, z) ≡ i+ j+ k,
∂x ∂y ∂z
en este caso, tenemos
T (x, y, z) = 2xi + 2y j − k,
de esta forma, en el punto (1, 1, 2) el gradiente est´ dado por
a
T (1, 1, 2) = 2i + 2j − k,
as´ que el mosquito deber´ moverse en la direcci´n del vector (2, 2, −1).
ı a o
b) Aplicando regla de la cadena, la raz´n de cambio en la temperatura esta
o
dada por:
dT dT ds
= ,
dt ds dt
donde
dT
= T · u,
ds
es la derivada direccional, y ds , es la rapidez con la que se mueve el mosquito.
dt
Por hip´tesis del problema, la direcci´n est´ dada por el vector unitario,
o o a
4i + 4 j − 2 k 4 4 2
u= √ = , ,− ,
16 + 16 + 4 6 6 6
de esta forma la derivada direccional estar´ dada por
a
dT 1 4 4 1
= (2, 2, −1) · (2, 2, −1) = + + = 3,
ds 3 3 3 3
ds
y como dt = 5, finalmente el cambio en la temperatura estar´ dada de la forma,
a
84

85. ◦
dT C
= 15 .
dt seg
85

86. Problema 15.
El capit´n Peluches tiene dificultades cerca del lado soleado de Mercurio.
a
La temperatura del casco de la nave, cuando ´l esta en la posici´n (x, y, z) est´
e o a
dada por:
T (x, y, z) = e−x−y−z ,
donde x, y y z est´n medidas en metros. Actualmente ´l est´ en el punto (2, 2, 2).
a e a
a) ¿En qu´ direcci´n deber´ avanzar para disminuir m´s rapido la temper-
e o a a
atura?
b) Si la nave viaja a e8 m , ¿con qu´ rapidez decaer´ la temperatura si avanza
s e a
en esa direcci´n?
o
Soluci´n:
o
a) Si el campo escalar de temperaturas, est´ dado por
a
T (x, y, z) = e−x−y−z ,
de la definici´n de la derivada direccional dT = T · u, que f´
o ds ısicamente nos da
la raz´n de cambio del campo escalar (temperatura) en la direcci´n del vector
o o
u, la m´xima raz´n de cambio de aumento de la temperatura estar´ dada por
a o a
dT
= | T|,
ds max
es decir, cuando T apunta en la direcci´n de u. Por lo tanto, si el capit´n
o a
Peluches est´ en el punto (2, 2, 2) se tiene que mover en direcci´n contraria al
a o
gradiente. Aplicando la definici´n del gradiente, tenemos
o
∂T ∂T ∂T
T = i+ j+ z
∂x ∂y ∂z
T = −e−x−y−z i − e−x−y−z j − e−x−y−z k
[T (2, 2, 2)] = −e−2−2−2 i + j + k = −e−6 i + j + k ,
de esta forma, el capit´n Peluches se tiene que mover en direcci´n del vector
a o
−6
e i+j+k .
b) Si la nave viaja una rapidez de e8 m/s ds , entoces la rapidez con la cual
dt
diminuye la temperatura, est´ dada por (aplicando regla de la cadena):
a
dT dT ds
= ,
dt ds dt
donde
dT
= T • u,
ds
y
86

87. T e−6 i + j + k i+j+k
u= = √ = √ ,
| T| e−12 3 3
por lo tanto,
2 √ 0
dT T | T| C
= T• = = | T | = e−6 3 ,
ds | T| | T| m
finalmente, la rapidez con la que disminuye la temperatura est´ dada por:
a
dT √ 0
C m √ 0
C
= 3 e8 = 3 e8 .
dt m s seg
87

88. Problema 16.
a) La temperatura en una caja rect´ngular est´ dada aproximadamente por
a a
T (x, y, z) = x(1 − x)(2 − y)(3 − z),
donde 0 < × < 1, 0 < y < 2 y 0 < z < 3. Si un mosquito se localiza en
el punto (0, 1, −2), en que direcci´n deber´ volar para enfriarse lo m´s r´pido
o a a a
posible. Explique su respuesta.
b) Si el mosquito est´ volando a una velocidad de 1.5 metros por segundo.
a
Con qu´ rapidez est´ cambiando la temperatura de la caja cuando se mueve en
e a
direcci´n paralela al eje x?.
o
Soluci´n.
o
a) El gradiante apunta donde la raz´n de cambio del incremento de tem-
o
peratura es m´xima, por lo que el mosquito debe moverse en direcci´n opuesta
a o
al gradiente. Por definici´n, el gradiente de una funci´n escalar est´ dado por,
o o a
∂T ∂T ∂T
T = i+ j+ k,
∂x ∂y ∂z
en este caso,
T (x, y, z) = x(1 − x)(2 − y)(3 − z),
luego entonces
∂T ∂T ∂T
T = i+ j+ k
∂x ∂y ∂z
T = [(1 − x) − x] (2 − y) (3 − z) i − x (1 − x) (3 − z) j − x (1 − x) (2 − y) k
= (1 − 2x) (2 − y) (3 − z) i − x (1 − x) (3 − z) j − x (1 − x) (2 − y) k
evaluando en el punto donde esta el mosquito, tenemos
T (0, 1, −2) = (1 − 2 (0)) (2 − (1)) (3 − (−2)) i + 0j + 0k
= 5i
es decir, el mosquito debe volar en direcci´n del vector −5 i para enfriarse.
o
m
b) Si el mosquito vuela a una rapidez de v = 1.5 seg = ds , entonces aplicando
dt
la regla de la cadena, tenemos
dT dT ds
= ,
dt ds dt
donde
dT
= T • u,
ds
y
88

89. u = (1, 0, 0)
puesto que se mueve en direcci´n paralela al eje x, por lo tanto
o
dT
= 1.5 ( T · u)
dt
= 1.5 5i · i ,
finalmente, la rapidez con la cual est´ cambiando la temperatura de la caja
a
cuando el mosquito se mueve en direcci´n paralela al eje x, est´ dada por
o a
0
dT C
= 7.5 .
dt seg
89

90. Problema 17.
a) Defina el concepto de conjunto de nivel.
b) Defina el concepto de gr´fica de una funci´n.
a o
c) Describa el comportamiento, conforme var´ c, del conjunto de nivel para
ıa
la siguiente funci´n.
o
f (x, y) = 1 − x2 − y 2 ,
d) Cual es el conjunto de nivel si c > 1.
Soluci´n:
o
a) Sea f : U ⊂ Rn −→ R, se define el conjunto de nivel como el conjunto
de puntos → ∈ U que satisfacen,
−
x
Lc = {→ ∈ U : f (→) = C ∈ R} .
−
x −
x
b) Sea
f : U ⊂ Rn −→ R,
se define la gr´fica de la funci´n f como el conjunto de puntos
a o
(x1 , x2 .........xn , f (x1 x2 , ....., xn )),
n+1
que pertenecen a R para
(x1 , x2 .........xn ) ∈ U,
es decir, el conjunto
((x1 , x2 ...., xn , f (x1 , x2 , ...., xn )) ∈ Rn+1 : (x1 , ..., xn ) ∈ U .
c) Si f (x, y) = 1 − x2 − y 2 ; en este caso el conjunto de nivel es una curva en
2
R tal que cumple:
Lc = (x, y) : 1 − x2 − y 2 = c ,
o tambi´n,
e
Lc = (x, y) : x2 + y 2 = 1 − c ,
√
es decir, conforme c varie las curvas del nivel son c´
ırculos de radio 1 − c.
d) Si c > 1 el conjunto de nivel es el conjunto vacio.
90

91. Problema 18.
Hallar un vector unitario normal a la superficie S representada por las ecua-
ciones param´tricas x = u cos v, y = u sin v, y z = z(u).
e
Soluci´n:
o
Por definici´n, una superficie S en el espacio est´ descrita por una funci´n
o a o
vectorial de la forma:
→(u, v) = x(u, v)i + y(u, v)j + z(u, v)k,
−
r
donde u y v son par´metros (variables), en forma an´loga al par´metro t para
a a a
→
−
una trayectoria curva en el espacio representada por f (t); as´ mismo, las ecua-
ı
ciones
x = x(u, v),
y = y(u, v),
z = z(u, v),
son las ecuaciones param´tricas de la superficie S.
e
En este caso, la ecuaci´n param´trica para la superficie S est´ dada por:
o e a
→(u, v) = u cos v i + u sin v j + z(u)k
−
r
por lo tanto, un vector normal unitario en cada punto de la superficie S repre-
sentada por la ecuaci´n anterior estar´ dado por:
o a
ru −v
→ ×→
− r
n= →− × → |,
|ru −v
r
donde los vectores →u y →v son vectores tangentes a las l´
−
r −
r ıneas coordenadas
u y v respectivamente, ´stos vectores est´n dados por:
e a
→
−
→ ≡ ∂ r (u, v) = cos v i + sin v j + z‘(u)k,
−
ru
∂u
y
→
−
→ ≡ ∂ r (u, v) = −u sin v i + u cos v j.
−rv
∂v
Calculando el producto vectorial de estos vectores, obtenemos
i j k
→ ×→ =
−
ru −v
r cos v sin v z‘(u) = (−u cos vz (u))i−(u sin vz (u))j+ u cos2 v + u sin2 v k
−u sin v u cos v 0
es decir,
→ × → = (−u cos vz (u))i − (u sin vz (u))j + uk,
−
ru −v
r
91

92. la magnitud de este vector est´ dada por,
a
|→u × →v | =
− − 2
r r (−u cos vz (u))2 + (u sin vz (u))2 + u2 = u 1 + [z (u)] ,
sustituyendo los resultados anteriores en la expresi´n para el vector unitario n,
o
obtenemos
− cos vz (u)i − sin vz (u)j + k
n=
2
1 + [z‘(u)]
Problema 19.
→
−
Demostrar que f = r 2 → es un campo vectorial conservativo y encontrar el
−
r
potencial escalar del cual se deriva.
Soluci´n:
o
→
−
Para mostrar que f = r 2 → es un campo conservativo debemos verifica que
−r
−
→ → −
× f = O.
→
−
Calculando el rotacional de f , usando la propiedad distributiva del producto
de un campo escalar por un campo vectorial obtenemos,
× (r 2 →) =
−
r r2 × → + r2
−
r × →,
−
r
aplicando las siguientes propiedades del operador nabla,
rn = nrn−2 →,
−
r
que se demuestra en el problema 22, y la propiedad
→
−
× → = O,
−
r
obtenemos,
→
−
× (r 2 →) = 2→ × → = O ,
−
r − −
r r
→
− −
es decir, f = r 2 →, es un campo vectorial conservativo.
r
→
−
Ahora debemos encontrar el potencial φ(r) tal que f (r) = φ(r). Para
hacer esto, aplicamos la siguiente expresi´n para el gradiente de una funci´n
o o
o −
que s´lamente depende de r = |→| , y que resulta de aplicar la regla de la
r
cadena,
∂φ(r) ∂φ(r) ∂φ(r)
φ(r) = i+ j+ k,
∂x ∂y ∂z
∂φ ∂r ∂φ ∂r ∂φ ∂r
= i+ j+ k,
∂r ∂x ∂r ∂y ∂r ∂z
= φ (r) r,
= φ (r)er ,
92

93. de esta forma, el campo vectorial dado, se puede escribir como,
→
−
f = r 2 → = r 3 er ,
−
r
por lo tanto, aplicando el hecho de que el campo vectorial es conservativo, es
→
−
decir f (r) = φ(r), obtenemos
φ (r) = r 3 ,
de donde, integrando obtenemos inmediatamente,
r4
φ(r) = + C,
4
donde C es una constante de integraci´n que depende de las condiciones iniciales.
o
93

94. Problema 20.
a) Mostrar que • [f (r)→] = 3f (r) + rf (r).
−
r
→] (no aplique la definici´n del determinante).
−
b) Calcule × [f (r) r o
Soluci´n:
o
Aplicando la propiedad de la divergencia del producto de una funci´n escalar
o
por una funci´n vectorial, dada por:
o
· [f (r)→] =
−
r f (r) · → + f (r) ·→,
−
r −
r
como el campo escalar f (r), s´lo depende de r = | r
o →| , podemos aplicar
−
→
−
r
f (r) = f (r) r = f (r)
,
r
adem´s, por definici´n de la divergencia de un campo vectorial, tenemos
a o
• → = 3,
−
r
entonces
→
−r →
• [f (r) →] = f (r)
−
r • − + 3f (r) = rf (r) + 3f (r),
r
r
b) En forma an´loga al inciso a) aplicando la propiedad del rotacional del
a
producto de una funci´n escalar por una funci´n vectorial, dada por:
o o
× [f (r)→] = f (r)
−
r ×→ +
−
r f (r) × →,
−
r
→
−
por definici´n, sabemos que
o × → = 0 , y aplicando la expresi´n para el
−
r o
gradiente de una funci´n que s´lamente depende de r, donde r = | →| , obtenemos
o o −
r
f (r) → → →
− ×− =−,
f (r) × → =
−
r r r 0
r
finalmente se demuestra que
→
−
× [f (r)→] = 0 .
−
r
94

95. Problema 21.
→
− →
− →
−
Hallar el campo vectorial F tal que F = f (r)→
−
r y div F = 0, es decir;
halle la funci´n f (r).
o
Soluci´n:
o
Aplicando la siguiente propiedad del operador nabla,
→
− →
− →
−
· ΦA = Φ· A +Φ · A,
en este caso, tenemos
Φ = f (r),
→
− →,
−
A = r
· [f (r)→] =
−
r f (r) · → + f (r) · →
−
r −
r
→| , podemos aplicar
−
como el campo escalar f, s´lo depende de r = | r
o
→
−
r
f (r) = f (r) r = f (r) ,
r
que se demuestra aplicando regla de la cadena (ver problema 19). Por otro lado,
de la definici´n de la divergencia de un campo vectorial, tenemos
o
∂ ∂ ∂
·→=
−
r , , · (x, y, z) = 3,
∂x ∂y ∂z
entonces
→
−r →
· [f (r)→] =
−
r f´ (r) · − + 3f (r)
r
r
= f´ (r)r + 3f (r),
aplicando la hip´tesis del problema dada por
o · [f (r) →] = 0, obtenemos
−
r
f´(r)
r + 3 = 0,
f (r)
o tambi´n,
e
1 3
df (r) = − dr,
f (r) r
integrando, obtenemos
95

96. df (r) dr
= −3
f (r) r
ln f (r) + cte = −3 (ln r + cte)
ln f (r) = ln r −3 + cte
−3
eln f (r) = e(ln r +cte) ,
finalmente, la funci´n escalar est´ dada por:
o a
A
f (r) = Ar −3 = .
r3
donde A es una constante de integraci´n.
o
96

97. Problema 22.
a) Si → = |→| demostrar las siguientes identidades,
−
r −
r
I) r n = nrn−2 →
−
r
2 n
II) r = n(n + 1)r n−2
III) · (r n →) = (n + 3) r n
−
r
b) Aplique los resultados del inciso a) para calcular,
1
I) r
2
II) ()1r 3/2
→
−r
III) · r3
Solucion:
a) Por definici´n, el vector de posici´n de un punto en el espacio est´ dado
o o a
por,
→ = xi + y j + z k,
−
r
de donde, la magnitud del vector esta dada por r = |→| = x2 + y 2 + z 2 .
−r
Aplicando la definici´n del operador vectorial nabla dado por,
o
∂ ∂ ∂
≡ i+ j+ k,
∂x ∂y ∂z
obtenemos para I),
∂rn ∂rn ∂rn
rn = i+ j+ k,
∂x ∂y ∂z
sustituyendo la magnitud del vector de posici´n, tenemos
o
∂ n ∂ n ∂ n
rn = x2 + y 2 + z 2 2 i + x2 + y 2 + z 2 2 j + x2 + y 2 + z 2 2 k
∂x ∂y ∂z
n 2 2
n
2 2 −1 n 2 2
n
2 2 −1 n 2 n
2 −1
= x +y +z (2x) i + x +y +z (2y) j + x + y2 + z2 (2z) k
2 2 2
n−2
= n x2 + y 2 + z 2 2
xi + y j + z k
= n |→|
− n−2 →,
r −
r
finalmente,
rn = nrn−2 →.
−
r
II) Para este caso, sabemos que el operador laplaciano est´ dado por,
a
97

98. 2 ∂2 ∂2 ∂2
≡ ·
+ 2 + 2,=
∂x2 ∂y ∂z
de esta forma, sustituyendo la magnitud del vector →, obtenemos
−r
2 n ∂2 n ∂2 n ∂2 n
r = x2 + y 2 + z 2 2
+ x2 + y 2 + z 2 2
+ x2 + y 2 + z 2 2
,
∂x2 ∂y 2 ∂z 2
observese por la forma de la funci´n escalar dada, s´lo necesitamos calcular
o o
las derivadas parciales con respecto a x, las derivada con respecto a y y z son
an´logas, sin embargo podemos usar el resultado del inciso anterior de la forma,
a
2 n
r ≡ · rn = · nrn−2 → ,
−
r
y en este caso podemos aplicar la siguiente propiedad del operador nabla,
→
− →
− →
−
· ΦA = Φ· A +Φ · A,
donde,
Φ = nr n−2 ,
→
−
A −
= →,
r
por lo tanto,
2 n
r ≡ · nrn−1 → =
−
r nrn−2 · → + nr n−2
−
r · →,
−
r
o −
aplicando la divergencia de una funci´n vectorial tenemos que · → = 3 y el
r
n−2 n−4 →
− , de esta forma,
resultado del inciso anterior, en este caso r = (n−2)r r
2 n
r = n(n − 2)r n−4 → · → + 3nr n−2 ,
− −
r r
n−2
= n(n − 2)r + 3nr n−2 ,
donde aplicamos el hecho de que → · → = |→| = r2 , finalmente obtenemos
− −
r r − 2
r
2 n
r = n(n + 2)r n−2 .
III). En forma an´loga al inciso a) parte II), aplicando la propiedad de
a
la divergencia de un campo escalar por un campo vectorial, en este caso las
funciones escalares y vectoriales est´n dadas por,
a
Φ = rn ,
→
− →,
−
A = r
por lo tanto,
98

99. · (r n →) =
−
r rn · → + rn
−
r ·→
−
r
usando los resultado de los incisos anteriores obtenemos,
· (r n →)
−
r = nr n−2 → · → + 3r n
− −
r r
= nr + 3r n
n
= (n + 3)r n .
b) Aplicando los resultados del inciso a) obtenemos,
→
−
I) 1
r = r−1 = (−1)r −3 → = − rr3 .
−
r
r− 2 = − 2 − 3 + 1 r(− 2 −2) = 3 r− 2 =
3 3 7
2 3 3
II) ()1r 3/2 = 2
2 4
√ .
4 r7
→
−
III) · rr3 = · r−3 → = 0.
−r
99

100. Problema 23.
Dado el campo vectorial,
→
− →
−r
F = → k,
−|
|r
→
−
donde → = xi + y j + z k. Para qu´ valor de la constante k, la divergencia de F
−
r e
es igual a cero?.
Soluci´n:
o
→
−
Las componentes del campo vectorial F est´n dadas por:
a
x
Fx = k ,
(x2 + y 2 + z 2 ) 2
y
Fy = k ,
(x2 + y 2 + z 2 ) 2
z
Fz = k ,
(x2 + y 2 + z 2 ) 2
→
−
como la divergencia de una campo vectorial F = Fx i + Fy j + Fz k, est´ dada
a
por
→ ∂Fx
− ∂Fy ∂Fz
·F ≡ + +
∂x ∂y ∂z
s´lamente necesitamos calcular una derivada parcial, de esta forma
o
∂Fx ∂ x
=
∂x ∂x (x2 + y 2 + z 2 ) k
2
k k
k 2 −1
x2 + y 2 + z 2 2
−x 2 x2 + y 2 + z 2 (2x)
= k
(x2 + y 2 + z2)
1 kx2
= k − k .
+1
(x2 + y 2 + z 2 ) 2 (x2 + y 2 + z 2 ) 2
An´logamente para las derivadas parciales con respecto a y y z, obtenemos
a
∂Fy 1 ky 2
= k − k .
∂y (x2 + y 2 + z 2 ) 2
(x2 + y 2 + z 2 ) 2
+1
∂Fz 1 kz 2
= k − k .
∂z (x2 + y 2 + z 2 ) 2 (x2 + y 2 + z 2 ) 2
+1
100

101. →
−
sumando los resultados anteriores, la divergencia del campo vectorial F ,
est´ dada por
a
→
− 3 k x2 + y 2 + z 2 3−k
·F = k − k = k .
+1
(x2 + y2 + z2) 2
(x2 + y2 + z2) 2 (x2 + y2 + z2 ) 2
→
−
de lo anterior, vemos que si k = 3, entonces la divergencia de F es igual a
cero.
101

102. Soluci´n alternativa:
o
Como el campo vectorial es de la forma,
→
−
F = f (r)→,
−
r
en este caso podemos aplicar la siguiente propiedad del operador nabla,
→
− →
− →
−
· f (r) A = f (r) · A + f (r) · A,
donde,
f (r) = |→| ,
− −k
r
→
− →,
−
A = r
de esta forma,
· − −k → =
|→|
r −
r |→|
r −
r −
− −k · → + |→|−k
r · →,
−
r
aplicando el resultado
df (r)
f (r) = er ,
dr
que se cumple para campos escalares que solamente dependen de r, donde r =
|→| . Por lo tanto,
−
r
→
−
· |→|
− −k →
r −
r = − −k−1 r · → + 3 |→|−k
− | →|
r −r −r
|→|
−
r
= − | →|
− −k−2 |→|2 + 3 |→|−k
r −
r −
r
3−k
= − k,
|→ |
r
donde se aplic´ tambi´n la propiedad de la norma del producto escalar de vec-
o e
tores y el hecho de que
∂x ∂y ∂z
·→=
−
r + + = 3.
∂x ∂y ∂z
→
−
De la misma forma, si k = 3, entonces · F = 0.
102

103. Problema 24.
Dado el campo vectorial,
→
− −y i + xj
F = k .
(x2 + y 2 ) 2
→
−
Hallar el valor de la constante k, de forma que F sea irrotacional, es decir
→ →
− −
que × F = 0 .
Soluci´n.
o
Aplicando la siguiente propiedad del operador nabla,
→
− →
− →
−
× ΦA = Φ× A +Φ × A,
donde en este caso,
−k
Φ = x2 + y 2 2
,
→
−
A = −y i + xj,
obtenemos,
k
−k −k
× x2 + y 2 2
−xi + y j = x2 + y 2 2
× −y i + xj + x2 + y 2 2
× −y i + xj ,
del problema anterior, obtenemos
−k −k
x2 + y 2 2
= k xi + y j
+1
(x2 + y2 ) 2
de esta forma,
−k −k −k
× x2 + y 2 2
−xi + y j = k xi + y j × −y i + xj + x2 + y 2 2
× −y i + xj
2 +1
(x2 + y 2 )
calculando el producto vectorial y el rotacional,
i j k
xi + y j × −y i + xj = x y 0 = x2 + y 2 k
−y x 0
i j k
∂ ∂
× −y i + xj = ∂x ∂y 0 = 2k
−y x 0
sustituyendo, obtenemos
103

104. k −k 2k
× x2 + y 2 2
−xi + y j = k x2 + y 2 k + k
+1
(x2 +y2) 2 (x2 + y2) 2
2−k
= k k.
(x2 + y 2 ) 2
→ →
− −
De lo anterior, si k = 2, entonces × F = 0.
104

105. Problema 25.
a) Calcular las constantes a, b y c, de forma que el campo vectorial
→
−
A = (x + 2y + az)i + (bx − 3y − z)j + (4x + cy + 2z)k
sea irrotacional.
b) Si el campo vectorial es irrotacional, encontrar el campo escalar del cual
se deriva ´ste campo vectorial .
e
Soluci´n:
o
→
− → →
− −
a) Por definici´n, si A es irrotacional debe cumplir que × A = 0 , por lo
o
tanto
i j k
→
− ∂ ∂ ∂
×A = ∂x ∂y ∂z
x + 2y + az bx − 3y − z 4x + cy + 2z
∂ ∂
= (4x + cy + 2z) − (bx − 3y − z) i
∂y ∂z
∂ ∂
− (4x + cy + 2z) − (x + 2y + az) j
∂x ∂z
∂ ∂
+ (bx − 3y − z) − (x + 2y + az) k
∂x ∂y
aplicando la hip´tesis de que el campo vectorial debe ser conservativo, entonces
o
c+1 = 0
−a + 4 = 0
b−2 = 0
de las ecuaciones anteriores obtenemos inmediatamente a = 4, b = 2 y c = −1.
Por lo tanto, el campo vectorial que es irrotacional est´ dado por:
a
→
−
A = (x + 2y + 4z)i + (2x − 3y − z)j + (4x − y + 2z)k
→ →
− − →
−
b) Debido a que si × A = 0 entonces, A = φ(x, y, z), por lo tanto
∂φ ∂φ ∂φ
(x + 2y + 4z)i + (2x − 3y − z)j + (4x − y + 2z)k = i+ j+ k,
∂x ∂x ∂x
105

106. de donde,
∂φ
= x + 2y + 4z,
∂x
∂φ
= 2x − 3y − z,
∂y
∂φ
= 4x − y + 2z,
∂z
Integrando parcialmente con respecto a x, y y z respectivamente, obtenemos:
x2
(1) φ(x, y, z) = 2 + 2xy + 4xz + f (y, z),
(2) φ(x, y, z) = 2xy − 3 y 2 − yz + g(x, z),
2
(3) φ(x, y, z) = 4xz − yz + z 2 + h(x, y),
derivando parcialmente con respecto a y, de las ecuaciones (1) y (2) obtenemos,
∂φ ∂f (y, z)
= 2x +
∂y ∂y
∂φ
= 2x − 3y − z
∂y
de las ecuaciones anteriores se obtiene,
∂f (y, z)
= −3y − z
∂y
integrando nuevamente con respecto a y obtenemos,
3
f (y, z) = − y 2 − yz + m(z)
2
substituyendo en la ecuaci´n (1) obtenemos,
o
x2 3
(4) φ(x, y, z) = 2 + 2xy + 4xz − 2 y 2 − yz + m(z).
Aplicando nuevamente el mismo procedimiento, es decir; de las ecuaciones
(3) y (4) derivando parcialmente con respecto a z, obtenemos
∂φ ∂m(z)
= 4x − y +
∂z ∂z
∂φ
= 4x − y + 2z
∂z
de lo anterior, se tiene
106

107. ∂m(z)
4x − y + = 4x − y + 2z
∂z
dm(z)
= 2z
dz
finalmente obtenemos,
m(z) = z 2 + cte,
→
−
por lo tanto, la funci´n escalar φ(x, y, z) tal que A =
o φ(x, y, z) est´ dada por:
a
x2 3
φ(x, y, z) = + 2xy + 4xz − y 2 − yz + z 2 + cte
2 2
n´tese que:
o
→
−
φ(x, y, z) = (x + 2y + 4z)i + (2x − 3y − z)j + (4x − y + 2z)k = A .
107

108. Problema 26.
a) Demostrar
→
−
A = (6xy + z 3 )i + (3x2 − z)j + (3xz 2 − y)k
que es irrotacional.
→
−
b) Hallar φ tal que A = φ.
Soluci´n:
o
a) Verifiquemos primeramente si el campo vectorial dado es irrotacional
i j k
→
− ∂ ∂ ∂
×A = ∂x ∂y ∂z
3 2 2
6xy + z 3x − z 3xz − y
∂ ∂
= (3xz 2 − y) − (3x2 − z) i
∂y ∂z
∂ ∂
− (3xz 2 − y) − (6xy + z 3 ) j
∂x ∂z
∂ ∂
+ (3x2 − z) − (6xy + z 3 ) k
∂x ∂y
= (−1 + 1)i − 3z 2 − 3z 2 j + (6x − 6x)k.
→ →
− − →
−
Por lo tanto como × A = 0 entonces A es irrotacional.
→
−
b) del resultado anterior, se tiene que A = φ por lo tanto
∂φ
= 6xy + z 3 ,
∂x
∂φ
= 3x2 − z,
∂y
∂φ
= 3xz 2 − y.
∂z
Integrando parcialmente con respecto a x, y y z respectivamente, obtenemos:
(1) φ(x, y, z) = 3x2 y + xz 3 + f (y, z),
108

109. (2) φ(x, y, z) = 3x2 y − yz + g(x, z),
(3) φ(x, y, z) = xz 3 − yz + h(x, y),
derivando parcialmente con respecto a z las ecuaciones (1) y (3) obtenemos,
∂φ ∂f (y, z)
= 3xz 2 + ,
∂z ∂z
∂φ
= 3xz 2 − y,
∂z
de las ecuaciones anteriores se obtiene,
∂f (y, z)
= −y,
∂y
integrando nuevamente con respecto a y obtenemos,
f (y, z) = −yz + m(y),
substituyendo en la ecuaci´n (1) obtenemos,
o
(4) φ(x, y, z) = 3x2 y + xz 3 − yz + m(y).
Aplicando nuevamente el mismo procedimiento, es decir; de las ecuaciones
(2) y (4) derivando parcialmente con respecto a y, obtenemos
∂φ ∂m(y)
= 3x2 − z + ,
∂y ∂y
∂φ
= 3x2 − z,
∂y
de lo anterior, se tiene
109

110. ∂m(y)
3x2 − z + = 3x2 − z,
∂y
dm(y)
= 0,
dy
finalmente obtenemos
m(z) = cte,
→
−
por lo tanto, la funci´n escalar φ(x, y, z) tal que A =
o φ(x, y, z) est´ dada por:
a
φ(x, y, z) = 3x2 y + xz 3 − yz + cte.
110

111. Problema 27.
Verificar si el campo vectorial
→
−
f = 3x2 y i + (x3 + 1)j + 9z 2 k
se puede obtener a partir del gradiente de una funci´n escalar. Si es as´
o ı,
obtenga el campo escalar.
Soluci´n:
o
→
−
Verifiquemos si el rotacional del campo vectorial dado es igual al vector 0 .
i j k
→
− ∂ ∂ ∂
× f = ∂x ∂y ∂z
,
2 3 2
3x y x + 1 9z
de lo anterior se deduce inmediatamente que,
→ →
− −
× f = 0.
Por lo tanto el campo vectorial es un campo conservativo, as´ que se puede
ı
deducir a partir del gradiente de una funci´n escalar, es decir;
o
−
→
f = φ.
→
−
De la expresi´n para el campo vectorial f y de la definici´n para el gradiente,
o o
obtenemos
∂φ
= 3x2 y,
∂x
∂φ
= x3 + 1,
∂y
∂φ
= 9z 2 .
∂z
111

112. Integrando parcialmente con respecto a x, y y z respectivamente, obtenemos:
(1) φ(x, y, z) = x3 y + f (y, z),
(2) φ(x, y, z) = x3 y + y + g(x, z),
(3) φ(x, y, z) = 3z 3 + h(x, y),
derivando parcialmente con respecto a x las ecuaciones (1) y (3) e igualando las
ecuaciones resultantes, obtenemos
∂h(x, y)
= 3x2 y
∂x
integrando nuevamente con respecto a x obtenemos,
h(x, y) = x3 y + m(y)
substituyendo en la ecuaci´n (3) obtenemos,
o
(4) φ(x, y, z) = 3z 3 + x3 y + m(y).
Aplicando nuevamente el mismo procedimiento, es decir; de las ecuaciones
(2) y (4) derivando parcialmente con respecto a y e igualando las ecuaciones
resultantes, obtenemos
dm(y)
=1
dy
finalmente obtenemos,
m(y) = y + cte
→
−
por lo tanto, la funci´n escalar φ tal que f = φ est´ dada por:
o a
φ(x, y, z) = 3z 3 + x3 y + y + cte.
112

113. Problema 28.
a) Demostrar que el campo vectorial definido por,
→ →
− −r
E = 2
r
es irrotacional.
→
−
b) Encontrar φ de forma que E = − φ, con la condici´n de que φ(a) = 0,
o
siendo a = cte > 0.
Soluci´n:
o
a) Para demostrar que el rotacional del campo vectorial dado es igual al
→
−
vector 0 , aplicaremos la siguiente propiedad del operador nabla
→
− →
− →
−
× φA = φ× A +φ ×A
→
−
en este caso, identificamos a φ = φ(r) = 1
r2 y A = →, aplicando la ecuaci´n
−
r o
anterior obtenemos:
→
−
r 1 1
× = r2
×→+
−
r × →,
−
r
r2 r2
aplicando la siguiente ecuaci´n
o
φ(r) = φ (r)er ,
que es v´lida para campos escalares donde r = |→|, obtenemos
a −
r
1 →
−
r
r2
=− ,
r
→
−
adem´s como
a × → = 0 . Al sustituir las expresiones anteriores, obtenemos
−
r
finalmente
→
− →
−
r →
−
×E = × r2
= 0
b) Como ya se demostr´ que
o
→ →
− −
×E = 0
entonces
→
−
E =− φ
aplicando nuevamente la ecuaci´n φ(r) = φ (r)er , identificando en este caso
o
correctamente la expresi´n para la funci´n escalar, obtenemos
o o
dφ(r) 1
=−
dr r
integrando, obtenemos
113

114. 1
φ(r) = − ln + cte
r
aplicando la condici´n de que φ(a) = 0 siendo a > 0, obtenemos el valor de la
o
constante de integraci´n dada por
o
cte = ln a
finalmente, obtenemos
a
φ(r) = ln .
r
114

115. Problema 29.
Considere la siguiente transformaci´n
o
x = w,
y = ev cos u,
z = ev sin u,
a) Calcule los factores de escala.
b) Verifique si el sistema de cordenadas (u, v, w) es ortogonal.
c) Hallar el elemento dS 2 .
Soluci´n:
o
a) En t´rminos de la transformaci´n dada, el vector de posici´n est´ dado
e o o a
por:
→ = wi + ev cos uj + ev sin uk.
−
r
Por definici´n, los factores de escala, est´n dados por:
o a
∂→
−
r
hu ≡ = e2v [sen2 u + cos2 u] = ev ,
∂u
∂→
−
r
hv ≡ = e2v cos2 u + sin2 u = ev ,
∂v
∂→
−
r
hw ≡ = 1.
∂w
b) Para verificar si el sistema es ortogonal debemos mostrar que
eu · ev = eu · ew = ev · ew = 0,
as´ como,
ı
eu · eu = ev · ev = ew · ew = 1.
Calculemos primero los vectores eu , ev y ew , que son los vectores unitarios
tangentes a las l´
ıneas coordenadas u, v y w respectivamente. Por definici´n o
tenemos,
∂ →/∂u
−
r ev sin uj + ev cos uk
eu ≡ = = − sin uj + cos uk,
|∂ →/∂u|
−
r e2v [sen2 u + cos2 u]
∂ →/∂v
−
r ev cos uj + ev sin uk
ev ≡ = = cos uj + sin uk,
|∂ →/∂v|
−
r e2v cos2 u + sin2 u
∂ →/∂w
−
r i
ew ≡ = = i,
|∂ →/∂w|
−
r i
115

116. de las ecuaciones anteriores, obtenemos
eu · e w = (− sin uj + cos uk) · (cos uj + sin uk)
= − sin u cos uj · j − sin2 uj · k + cos2 uk · j + sin u cos uk · k
= 0
tambi´n, en forma inmediata se observa que se cumple
e
ev · ew = eu · ev = 0,
as´ como
ı
eu · e u = e v · e v = e w · e w = 1
c) Por definici´n, el elemento dS 2 est´ dado por,
o a
dS 2 = d→ · d→,
− −
r r
donde
∂→
−
r ∂→
−
r ∂→
−
r
d→ =
−
r du1 + dv + dw,
∂u ∂v ∂w
→
− →
− →
−
los vectores, ∂ r , ∂ r y ∂ r son vectores tangentes a las l´
∂u ∂v ∂w ıneas coordenada u,
v y w respectivamente y est´n dados por
a
∂→
−
r
= ev sin uj + ev cos uk
∂u
∂→
−
r
= ev cos uj + ev sin uk
∂v
∂→
−
r
= i
∂w
De esta forma, el elemento dS 2 est´ dado por,
a
dS 2 = dw2 + e2v sin2 udu2 − 2 sin udu cos udv + sin2 udu2
+e2v cos2 udu2 + 2 cos udv sin udv + sin2 udv 2
= dw2 + e2v sin2 udu2 + e2v cos2 udv 2 + e2v cos2 udu2 + e2v sin2 udv 2
= du2 e2v sin2 u + cos2 u + dv 2 e2v cos2 u + sin2 u + dw2
dS 2 = e2v du2 + e2v dv 2 + dw2 .
Con lo cual se comprueba que es ortogonal, ya que no hay t´rminos cruzados.
e
116

117. Problema 30.
Encuentre la relaci´n de los vectores unitarios en coordenadas esf´ricas y
o e
rect´ngulares, es decir, encuentre:
a
i = i (er , eθ , eφ ) ,
j = j (er , eθ , eφ ) ,
k = k (er , eθ , eφ ) ,
y
er = er i, j, k ,
eθ = eθ i, j, k ,
eφ = eφ i, j, k ,
Soluci´n:
o
La transformaci´n entre cordenadas rect´ngulares y esf´ricas est´ dada por:
o a e a
x = r sin θ cos φ,
y = r sin θ sin φ,
z = r cos θ
donde, 0 ≤ θ ≤ π, 0 ≤ φ ≤ 2π y 0 ≤ r. El vector de posici´n de un punto en
o
el espacio en coordenadas esf´ricas est´ dado por:
e a
→ = r sin θ cos φi + r sin θ sin φj + r cos θ k
−
r
de esta forma, los vectores unitarios tangentes a las l´
ıneas coordenadas r, θ y
φ est´n dados por,
a
∂→
−
r
∂r sin θ cos φi + sin θ sin φj + cos θ k
er = →
− = ,
∂r
∂r sin2 θ cos2 φ + sin2 θ + cos2 θ
∂→
−
r
∂φ r cos θ cos φi + r cos θ sin φj − r sin θ k
eθ = = ,
∂→
−
r
∂θ r2 cos θ 2 sin2 φ + sin2 φ − r2 sin2 θ
∂→
−
r
∂φ −r sin θ sin φi + r sin θ cos φj
eφ = = ,
∂→
−
r
∂φ r2 sin2 θ sin2 φ cos2 φ
117

118. que se pueden escribir finalmente de la forma,
(a) er = sin θ cos φi + sin θ sin φj + cos θ k,
(b) eθ = cos θ cos φi + cos θ sin φj − sin θ k,
(c) eφ = − sin φi + cos φj.
Ahora para encontrar la dependencia de los vectores i, j y k, en t´rminos
e
de los vectores er , eθ y eφ , aplicamos la siguiente relaci´n vectorial
o
→
− →
− →
− →
−
A = A · u 1 u1 + A · u 2 u2 + A · u 3 u3 ,
→
−
para cualquier vector A , que es v´lida para los vectores u1 , u2 y u3 , que
a
forman una base ortonormal, es decir que cumplen que u i · uj = δij , donde δij
es la funci´n delta de Kcronecker y est´ dada por,
o a
1, i = j
δij =
0, i = j
De esta forma, como los vectores unitarios i, j y k y er , eθ y eφ forman
una base ortonormal, aplicando la expresi´n anterior escribimos a los vectores
o
i, j y k en t´rminos de los vectores er , eθ y eφ de la forma,
e
(1) i = i · e r er + i · e θ eθ + i · e φ eφ ,
(2) j = j · e r er + j · e θ eθ + j · e φ eφ ,
(3) k = k · e r er + k · e θ eθ + k · e φ eφ ,
por otro lado de las ecuaciones (a), (b) y (c), aplicando la de definici´n del
o
producto escalar, obt´nemos
e
i · er = sin θ cos φ, i · eθ = cos θ cos φ, i · eφ = − sin φ,
j · er = sin θ sin φ, j · eθ = cos θ sin φ, j · eφ = cos φ,
k · er = cos θ, k · eθ = − sin θ, k · eφ = 0,
sustituyendo los resultados anteriores en las ecuaciones (1), (2) y (3), final-
118

119. mente se obtiene
i = sin θ cos φer + cos θ cos φeθ − sin φeφ
j = sin θ sin φer cos θ sin θeθ − cos φeφ
k = cos θer − sin θeφ .
Problema 31.
Transformar la siguiente funci´n vectorial
o
→
− 1
f = eϕ ,
rsenθ
que est´ en cordenadas esf´ricas (r, θ, φ), a coordenadas rect´ngulares.
a e a
Soluci´n:
o
Por definici´n, las coordenadas esf´ricas est´n dadas por la transformaci´n:
o e a o
x = r sin θ cos ϕ,
y = r sin θ sin ϕ,
z = r cos θ,
por lo tanto, el vector de posici´n de un punto en el espacio en coordenadas
o
esf´ricas, est´ dado por:
e a
→ = xi + y j + z k = r sin θ cos ϕi + r sin θ sin ϕ + r cos θ,
−
r
de esta expresi´n, debemos calcular primero el vector unitario tangente a la
o
l´
ınea coordenada ϕ de la forma,
∂ →/∂ϕ
−
r −r sin θ sin ϕi + r sin θ cos ϕj
eϕ ≡ →/∂ϕ| =
|∂ −
r (r sin θ sin ϕ)2 + (r sin θ cos ϕ)2
−r sin θ sin ϕi + sin θ cos ϕj
= ,
r2 sin2 θ(sin2 ϕ + cos2 ϕ)
por lo tanto,
eϕ = − sin ϕi + cos ϕj,
→
−
sustituyendo en la expresi´n para f , obtenemos
o
→
− 1 1
f = eϕ = (− sin ϕi + cos ϕj),
r sin θ r sin θ
y de las ecuaciones de transformaci´n, obtenemos:
o
119

120. y
sin ϕ = ,
r sin θ
x
cos ϕ = ,
r sin θ
sustituyendo, obtenemos
→
− y x
f =− 2 i+ 2 j,
r2sin θ r sin2 θ
por otro lado, de las ecuaciones de transformaci´n tambi´n tenemos que,
o e
x2 + y 2 = r2 sin2 θ,
finalmente, sustituyendo la ecuaci´n anterior obtenemos
o
→
− y x
f =− i+ 2 j.
x2 +y 2 x + y2
120

121. Problema 32.
Transformar la funci´n vectorial
o
→
−
F = ρeρ + ρeφ ,
que est´ en coordenadas cil´
a ındricas, a coordenadas rectangulares.
Soluci´n:
o
El vector de posici´n de un punto P en el espacio esta dado por
o
→ = xi + y j + z k
−
r
sustituyendo las ecuaciones de transformaci´n de coordenadas cil´
o ındricas y rect´ngulares,
a
dadas por las ecuaciones
x = ρ cos φ,
y = ρ sin φ,
z = z,
obtenemos
−
→ = ρ cos φi + ρ sin φj + z k,
r
por lo tanto, los vectores unitarios tangentes a las l´
ıneas coordenadas ρ y φ
est´n dados por:
a
∂→
−
r
∂ρ cos φi + sin φj
eρ ≡ = = cos φi + sin φj,
∂→
−
r cos φ2 + sin φ2
∂ρ
∂→
−
r
∂φ −ρ sin φi + ρ cos φj
eφ ≡ = = − sin φi + cos φj,
∂→
−
r ρ2 cos φ2 + ρ2 sin φ2
∂φ
De la transformaci´n inversa, tenemos
o
1
ρ = x2 + y 2 2
,
sustituyendo las expresiones para los vectores unitarios e ρ y eφ , y la ecuaci´n
o
anterior, en la funci´n vectorial, obtenemos
o
→
− 1 1
F = x2 + y 2 2
cos φi + sin φj + x2 + y 2 2
− sin φi + cos φj
1
= x2 + y 2 2
cos φi + sin φj − sin φi + cos φj
1
= x2 + y 2 2
(cos φ − sin φ) i + (sin φ + cos φ) j
y de las ecuaciones de transformaci´n, obtenemos
o
121

122. →
− 1 x y x y
F = x2 + y 2 2
1 − 1 i+ 1 + 1 j
(x2 + y 2 ) 2
(x2 + y 2 ) 2
(x2 + y 2 ) 2
(x2 + y 2 ) 2
finalmente se obtiene,
→
−
F = (x − y)i + (x + y)j
122

123. Problema 33.
Para las coordenadas cil´
ındricas parab´licas (ξ, η, φ), las ecuaciones de trns-
o
formaci´n a coordenadas rect´ngulares est´n dadas por,
o a a
x = ξη cos φ,
y = ξη sin φ,
1 2
z = η − ξ2 .
2
a) Hallar los factores de escala.
b) Mostrar que eη × eξ = eφ .
Soluci´n:
o
a) Por definici´n sabemos que el vector de posici´n de un punto en el espacio
o o
est´ dado por,
a
→ = xi + y j + z k,
−
r
sustituyendo las ecuaciones de transformaci´n, tenemos
o
→ (ξ, η, φ) = ξη cos φi + ξη sin φj + 1 η 2 − ξ 2 k,
−r
2
de donde, los factores de escala est´n dados por,
a
∂→
−
r
hξ ≡ = η 2 cos2 φ + η 2 sin2 φ + ξ 2 = η2 + ξ2 ,
∂ξ
∂→
−
r
hη ≡ = ξ 2 cos2 φ + ξ 2 sin2 φ + η 2 = ξ2 + η2,
∂η
∂→
−
r
hφ ≡ = sin2 φ + cos2 φ = 1.
∂φ
b) Por definici´n, los vectores unitarios tangentes a las l´
o ıneas coordenadas ξ,
η y φ para este caso est´n dados por,
a
123

124. ∂→
−
r
∂ξ η cos φi + η sin φj − ξ k
eξ ≡ = ,
∂→
−
r η2 + ξ2
∂ξ
∂→
−
r
∂η ξ cos φi + η sin φj − η k
eη ≡ = ,
∂→
−
r η2 + ξ2
∂η
∂→
−
r
∂ξ − sin φi + cos φj
eξ ≡ = ,
∂→
−
r 1
∂ξ
tambi´n se pueden representar de la siguiente forma,
e
1
eξ = η cos φi + η sin φj − ξ k ,
hξ
1
eη = ξ cos φi + ξ sin φj − η k ,
hη
eφ = − sin φi + cos φj.
Por lo tanto, calculando el producto vectorial de los vectores unitarios e ξ y
eη , obtenemos
1 1 i j k
eξ × e η = η cos φ η sin φ −ξ
hξ hη
ξ cos φ ξ sin φ η
1
= η 2 sin φ + ξ 2 sin φ i − η 2 cos φ + ξ 2 cos φ j
(η 2 + ξ 2 )
1
= 2 + ξ2)
η 2 + ξ 2 sin φi − η 2 + ξ 2 cos φj
(η
= sin φi − cos φj = eφ .
124

125. 4 Problemas del cap´
ıtulo 3.
Problema 1.
Si φ(x, y) = xy Calcular φd→ desde el punto (0, 0, 0) hasta el punto (1, 1, 0)
−
r
a lo largo de:
a) La curva y = x2 , z = 0.
b) La l´
ınea recta que une los puntos (0, 0, 0) y (1, 1, 0).
Soluci´n:
o
a) La ecuaci´n de la par´bola y = x2 , z = 0, se puede representar en forma
o a
param´trica de la forma,
e
→(t) = ti + t2 j
−
r
donde 0 ≤ t ≤ 1. Por lo tanto el elemento de desplazamiento diferencial d →
−
r
est´ dado por:
a
d→(t) = dti + 2tdtj
−
r
as´ la integral de l´
ı ınea resulta,
(1,1,0) 1
−
φd→
r = φ(x, y)d→ =
−
r t t2 dti + 2tdtj
C (0,0,0) t=0
1 1
= i t3 dt + j 2t4 dt
t=0 t=0
al resolver la integral, obtenemos
1 2
φd→ =
−
r i+ j
C 4 5
b) Recordemos que la ecuaci´n param´trica de una recta que pasa por dos
o e
puntos est´ dada por:
a
→(t) = → + t (→ − → ) ,
−
r −
r1 −
r2 −1
r
125

126. donde →1 y →2 son los vectores de posici´n de los puntos (x1 , y1 , z1 ) y (x2 , y2 , z2 )
−
r −
r o
respectivamente por donde pasa la recta. En este caso los puntos son: (0, 0, 0)
y (1, 1, 0), por lo tanto la ecuaci´n de la recta en forma param´trica que va del
o e
punto (0, 0, 0) y (1, 1, 0) est´ dada por,
a
→(t) = t (1, 1, 0) ,
−
r
es decir,
→(t) = ti + tj,
−
r
as´ en este caso el vector de desplazamiento diferencial est´ dado por:
ı, a
−
d→(t) = dti + dtj
r
la integral de l´
ınea resulta,
(1,1,0) 1
φd→
−
r = φ(x, y)d→ =
−
r t2 dti + dtj
C (0,0,0) t=0
1 1
= i t2 dt + j t2 dt
t=0 t=0
finalmente al resolver la integral, obtenemos
1 1
φd→ =
−
r i+ j
C 3 3
Soluciones alternativas:
a) La curva est´ descrita por las ecuaciones,
a
y = x2
z = 0.
126

127. Si escogemos a la variable x como par´metro, entonces las ecuaciones param´tricas
a e
de la curva dada son :
x = x
y = x2 ,
por lo que la ecuaci´n de la cuva en forma param´trica est´ dada por:
o e a
→(x) = xi + x2 j;
−
r 0≤x≤1
de donde obtenemos,
d→ = dxi + 2xdxj
−
r
por lo que la integral se puede calcular de la siguiente forma:
(1,1,0)
1
1 2
φd→ =
−
r x3 (dxi + 2xdxj) = ... = i + j.
0 4 5
(0,0,0)
An´logamente, si escogemos a y como par´metro, las ecuaciones param´tricas
a a e
ser´n:
a
√
x = y
y = y,
por lo que la ecuaci´n de la cuva en forma param´trica est´ dada por:
o e a
→(y) = √y i + y j;
−
r 0≤y≤1
de donde obtenemos,
1
d→ = √ dy i + dy j,
−
r
2 y
por lo que la integral se puede calcular de la siguiente forma:
127

128. (1,1,0)
1
1
φd→ =
− 5
r y 2 ( √ dy i + dy j)
0 2 y
(0,0,0)
al hacer un poco de algebra, obtenemos
´
(1,1,0)
1 1
y
φd→
− 5
r = i dy + j y 2 dy
0 2 0
(0,0,0)
1 1
y2 2 5
= i +j y2
4 0 5 0
1 2
= i+ j
4 5
b) An´logamente al inciso a) de la soluci´n alternativa si escogemos a la
a o
variable x como par´metro la ecuaci´n param´trica de la curva est´ dada por:
a o e a
→(x) = xi + xj;
−
r 0≤x≤1
de donde obtenemos,
d→ = dxi = dxj,
−
r
finalmente, al resolver la integral de l´
ınea se obtiene,
(1,1,0)
1 1
φd→ =
−
r x2 (dxi + dxj) = ... = i + j.
(0,0,0) 3 3
128

129. Problema 2.
Calcular C φd→ para φ = x3 y +zy desde el punto (1, 1, 0) al punto (2, 4, 0) ,
−
r
a) a lo largo de la parabola y = x2 z = 0,
b) la recta que une (1, 1, −0) y (2, 4, 0) .
Soluci´n:
o
a) Si tomamos como par´metro a x, donde 1 ≤ x ≤ 2, la ecuaci´n de la
a o
par´bola en forma param´trica est´ dada por:
a e a
→(x) = xi + x2 j,
−
r
por lo tanto, el elemento diferencial de l´
ınea est´ dado por,
a
d→ = dxi + 2xdxj,
−
r
luego entonces,
(2,4,0)
φd→ =
−
r x3 y + zy d→,
−
r
C (1,1,0)
sustituyendo la parametrizaci´n de la trayectoria, obtenemos
o
2
φd→
−
r = x3 x2 + 2x2 dxi + 2xdxj
C 1
2 2
= x5 + 2x2 dxi + 2xdxj = x5 + 2x2 dxi + x5 + 2x2 (2x) dxj
1 1
2 2
= x5 + 2x2 dxi + 2x6 + 4x3 dxj
1 1
2 2
x6 2 2 7
= + x3 i+ x + x4 j
6 3 1 7 1
3
26 2 (2) 1 2 2 7 4 2 7 4
= + − + i+ (2) + (2) − (1) + (1) j
6 3 6 3 7 7
64 + 32 − 1 − 4 256 + 112 − 2 − 7
= i+ j,
6 7
finalmente, se obtiene
91 359
φd→ =
−
r , ,0
C 6 7
129

130. b) Se sabe que la ecuaci´n param´trica de una recta que pasa por dos puntos
o e
est´ dada por:
a
→(t) = → + t (→ − → ) ,
−
r −
r1 −
r2 −1
r
donde →1 y →2 son los vectores de posici´n de los puntos (x1 , y1 , z1 ) y (x2 , y2 , z2 )
−
r −
r o
respectivamente por donde pasa la recta. En este caso los puntos son: (1, 1, 0)
y (2, 4, 0), por lo tanto la ecuaci´n de la recta en forma param´trica que va del
o e
punto (1, 1, 0) al punto (2, 4, 0) est´ dada por,
a
→(t) = (1, 1, −0) + t (1, 3, 0) ,
−
r
donde 0 ≤ t ≤ 1, o tambi´n,
e
→(t) = (1, t + 3t, 0) ,
−
r
as´ en este caso el vector de desplazamiento diferencial est´ dado por:
ı, a
d→(t) = dti + 3dtj,
−
r
y las ecuaciones param´tricas de la recta est´n dadas por:
e a
x = 1 + t,
y = 1 + 3t,
z = 0.
De esta forma, sustituyendo las ecuaciones parametricas la funci´n φ est´
o a
dada por:
3
φ = (1 + t) (1 + 3t) + 2 + 6t,
por lo tanto,
130

131. (2,4,0)
φd→
−
r = x3 y + zy d→ =
−
r
C (1,1,0)
t=1
3
= (1 + t) (1 + 3t) + 2 + 6t dti + 3dtj
t=0
t=1
= 1 + 3t + 3t2 + t3 (1 + 3t) + 2 + 6t dti + 3dtJ
t=0
t=1 t=1
= 3 + 12t + 12t2 + 10t3 + 3t4 dti + 3 3 + 12t + 12t2 + 10t3 + 3t4 dtJ
t=0 t=0
1 1
5 3 5 3
= 3t + 6t2 + 4t3 + t4 + t5 i + 3 3t + 6t2 + 4t3 + t4 + t5 j
2 5 0 2 5 0
5 3 5 3
= 3+6+4+ + −0 i+3 3+6+4+ + −0 j
2 5 2 5
30 + 60 + 40 + 25 + 6 30 + 60 + 40 + 25 + 6
= i+3 j
10 10
finalmente, se obtiene
161 483
φd→ =
−
r i+ j.
C 10 10
131

132. Problema 3.
→ −
− →
−
Calcular c f · d→ para f = y i + (x + z) j + (x − z) k desde el punto
2 2
r
(0, 0, 0) al punto (2, 4, 0),
a) a lo largo de la parabola y = x2 z = 0,
b) la recta y = 2x.
Soluci´n:
o
En forma an´loga al problema anterior, si tomamos como par´metro a x,
a a
donde 0 ≤ x ≤ 2, las ecuaciones param´tricas de la curva est´n dadas por:
e a
x = x
y = x2
z = 0
as´ la ecuaci´n param´trica de la par´bola est´ dada por,
ı, o e a a
→(x) = xi + x2 j,
−
r
por lo tanto, el elemento diferencial de l´
ınea est´ dado por,
a
−
d→ = dxi + 2xdxj
r
de esta forma, la integral de l´
ınea esta dada por:
(2,4,0)
→ →
− − 2 2
f ·dr = y i + (x + z) j + (x − z) k · dxi + 2xdxj
c (0,0,0)
2
= 2
x i + x2 j + x2 k · dxi + 2xdxj
0
2 2
= x2 dx + x2 (2x) dx = x2 + 2x3 dx
0 0
2
x3 2x4
= +
3 4 0
3 4
2 (2)
= +2
3 4
finalmente, obtenemos
→ → 128
− − 32
f ·dr = = .
C 12 3
132

133. b) En forma an´loga, si tomamos a x, como parametro, la ecuaci´n de la
a o
recta en forma param´trica est´ dada por,
e a
→(x) = xi + 2xj,
−
r
donde 0 ≤ x ≤ 2, por lo tanto, el elemento diferencial de l´
ınea en este caso est´
a
dado por,
d→ = dxi + 2dxj,
−
r
de esta forma, la integral de l´
ınea esta dada por:
2
→ →
− −
f ·dr = 2xi + x2 j + x2 k · dxi + 2dxj
c 0
2 2
2
= 2x + 2x2 dx = x2 + x3
0 3 0
3
2 (2)
= 4+
3
28
= .
3
133

134. Problema 4.
→
− → →
−
Dado el campo vectorial F = 3xi + (2xz − y) j + z k. Calcular C
F · d−
r
desde el punto (0, 0, 0) hasta (2, 1, 3) a lo largo de,
a) la curva x = 2t2 , y = t, z = 4t2 − t, para 0 ≤ t ≤ 1.
b) La recta que une a esos puntos.
Soluci´n:
o
La ecuaci´n de la curva en forma param´trica est´ dada por:
o e a
→(t) = 2t2 i + tj + 4t2 − t k,
−
r
donde 0 ≤ t ≤ 1, por lo tanto el elemento diferencial de l´
ınea est´ dado por:
a
d→(t) = 4tdti + dtj + (8t − 1)dtk.
−
r
Por lo tanto, la integral de l´
ınea est´ dada por:
a
(1,1,0)
→ →
− − →
−
F ·dr = F (x, y, z) · d→(x, y, z)
−
r
C (0,0,0)
t=1
= [3 2t2 i + 2 2t2 4t2 − t − t j + 4t2 − t k] ·
t=0
[4tdti + dtj + (8t − 1)dtk)]
haciendo un poco de algebra obtenemos,
´
1 1 1 1 1
→ →
− −
F ·dr = 24 t3 dt + 16 t4 dt − 4 t3 dt + 32 t3 dt − 12 t2 dt
C 0 0 0 0 0
1
16 5
= 6t4 + t − t4 − t2 + 8t4 − 4t3 + t2
5 0
1
16 5
= t + 13t4 − 4t3
5 0
16 16 + 65 − 20
= + 13 − 4 =
5 5
61
= .
5
134

135. Problema 5.
Calcular → × d→ a lo largo de la trayectoria representada por la ecuaci´n,
−
r −
r o
C
x2 + 2x + y 2 = 9.
Solucion:
Completando cuadrados en la ecuaci´n de la trayectoria, obtenemos
o
2
(x + 1) + y 2 = 10,
√
que es la ecuaci´n de un c´
o ırculo con centro en el punto (−1, 0) y radio 10. Las
ecuaciones param´tricas de esta trayectoria est´n dadas por,
e a
√
x = −1 + 10 cos θ,
√
y = 10 sin θ,
donde 0 ≤ θ ≤ 2π. Por lo tanto, la ecuaci´n de la trayectoria en forma
o
param´trica est´ dada por,
e a
→(θ) = (−1, 0) + √10 cos θ i + √10 sin θ j,
−
r
de donde, el elemento diferencial de l´
ınea est´ dado por,
a
√ √
d→ = − 10 sin θ i + 10 cos θ j.
−
r
Calculando el producto vectorial de → y d→ obtenemos,
−
r −
r
→×d→ =
− − √ i √ j k √ 2 √ 2
r r = 10 cos2 θ+ 10 sin2 θk = 10k,
√ cos θ
10 √ 10 sin θ 0
− 10 sin θ 10 cos θ 0
de esta forma, la integral de l´
ınea est´ dada por,
a
2π
→ × d→ =2π 10dθ k = 10kθ
−
r −
r θ=0 = 20π k.
θ=0
C
135

136. Problema 6.
Dada la funci´n vectorial
o
→
−
A = (y − 2x)i + (3x + 2y)j,
→
−
hallar la integral de l´
ınea de A a lo largo de la trayectoria C, que es un c´
ırculo
en el plano XY con centro en el origen y radio 2, sabiendo que C se recorre en
sentido negativo, es decir en sentido de las manecillas del reloj.
Soluci´n:
o
Y
0
X
Como se observa en la figura, y debido a que la trayectoria se recorre en
sentido a favor de las manecillas del reloj, las ecuaciones param´tricas de la
e
trayectoria C est´n dadas por:
a
x = 2 cos θ,
y = −2 sin θ,
donde
0 θ
2π,
→ −
−
ınea est´ definida por A •d→, debemos de calcular primero
como la integral de l´ a r
ınea d→. El vector de posici´n en cualquier punto de
el elemento diferencial de l´ −r o
la trayectoria C est´ dado por r
a → = 2 cos θ i − 2 sin θ j, de donde obtenemos,
−
d→ = −2 sin θdθ i − 2 cos θdθ j,
−
r
asimismo, el campo vectorial est´ dado por,
a
→
−
A = (−2 sin θ − 4 cos θ) j + (6 cos θ − 4 sin θ) j,
136

137. por lo tanto,
→ →
− −
A · d r = 4 sin2 θ + 4 sin θ cos θ) + (8 sin θ cos θ − 12 cos θ 2 ) dθ,
de esta forma la integral de l´
ınea est´ dada por,
a
2π
→ →
− −
A ·dr = sin2 θ + 12 sin θ cos θ − 12 cos2 θ dθ
c θ=0
2π 2π
= 4 sin θ cos θdθ − 12 cos2 θdθ
θ=0 θ=0
2π 2π 2π
θ sin 2θ sin2 θ θ sin 2θ
= 4 − + 12 − 12 +
2 4 θ=0 2 θ=0 2 4 θ=0
2π 2π
= 4 − 12 = −8π.
2 2
Notese que si la trayectoria C se recorre en sentido positivo, las ecuaciones
param´tricas de C estar´ dadas por x = 2 cos θ y y = 2 sin θ, y por lo tanto,
e ıan
el resultado ser´ de la forma
ıa
→ →
− −
A · d r = 8π.
c
137

138. Problema 7.
Dado el siguiente campo vectorial
→
− y x
F (x, y) = i− 2 j,
x2 + y 2 x + y2
→
−
calcular la integral de la componente tangencial de F de (−1, 0) a (1, 0);
a) A lo largo del semic´ ırculo que une esos puntos,
b) A lo largo de la trayectoria poligonal que se muestra en la siguiente figura.
Y
C2
(0,1) (1,1)
C
1
C3
X
(−1,0) (1,0)
Soluci´n:
o
a) Sabemos que x2 + y 2 = 1, es la ecuaci´n de un c´
o ırculo de radio 1, entonces
la ecuaci´n del semic´
o ırculo ser´
ıa:
y= 1 − x2 ,
si escogemos a x como par´metro, entonces la ecuaci´n del la trayectoria curva
a o
que es el semic´
ırculo est´ dada por:
a
→(x) = xi +
−
r 1 − x2 j
donde −1 ≤ x ≤ 1, de la ecuaci´n anterior el elemento diferencial de l´
o ınea est´
a
dado por:
xdx
d→ = dxi + √
−
r (−2x)dxj
1 − x2
es decir,
xdx
d→ = dxi −
−
r √j
1 − x2
→
−
por lo tanto, la componente tangencial de F a lo largo del semic´
ırculo
(1,0) 1 √
→ →
− − 1 − x2 −x x
F ·dr = + −√ dx
x2 + 1 − x 2 x2 + 1 − x2 1 − x2
(−1,0) −1
138

139. (1,0) 1 1
→ →
− − x2 dx
F ·dr = 1− x2 +√ dx = √ .
1 − x2 1 − x2
(−1,0) −1 −1
La integral anterior es del tipo de integrales que se resuelven con cambios
de variable trigonom´tricos y es relativamente sencilla. Antes de resolver la
e
integral, observemos que se puede resolver seleccionando adecuadamente la
parametrizaci´n de la trayectoria.
o
En este caso, sabemos que
x(θ) = cos θ,
y(θ) = sin θ,
donde 0 ≤ θ ≤ 2π, son las ecuaciones param´tricas de un c´
e ırculo de radio 1.
Por lo tanto la ecuaci´n en forma param´trica de la trayectoria semicircular est´
o e a
dada por:
→(θ) = cos θ i + sin θ j;
−
r θ ∈ [0, π]
observe que el par´metro θ no va de 0 a π. De la ecuaci´n anterior, el elemento
a o
diferencial de l´
ınea est´ dado por:
a
d→(θ) = − sin θdθ i + cos θdθ j.
−
r
→
−
Por lo tanto, la integral de l´
ınea de la componente tangencial del campo F
a lo largo de la trayectoria semicircular resulta ser,
(1,0) θ=0
→ →
− −
F ·dr = cos θ i + sin θ j · − sin θdθ i + cos θdθ j
(−1,0) θ=π
0 π
2 2
= − (Sen θ + Cos θ)dθ = dθ = π.
π 0
Este ultimo resultado muestra que la selecci´n adecuada de la parametrizaci´n
´ o o
de la trayectoria semicircular conduce a un resultado relativamente m´s facil
a
que la selecci´n del par´metro x.
o a
Por otro lado, notemos que para encontrar la integral de l´ınea para el inciso
b) tenemos que resolver dicha integral en tres partes de la forma;
(1,0)
→ →
− − → →
− − → →
− − → →
− −
F ·dr = F ·dr + F ·dr + F ·dr
C1 C2 C3
(−1,0)
donde C1 , C2 y C3 son las integrales de l´
ınea a lo largo de las trayectorias
rectas como se muestran en la figura. La ecuaci´n anterior sin necesidad de
o
139

140. hacer c´lculos muestran que el procedimiento es un poco laborioso. Por lo
a
tanto, analizemos el campo vectorial dado.
→
−
Si calculamos el rotacional de F obtenemos:
i j k
→
− ∂ ∂ ∂
×F = ∂x ∂y ∂z
y x
x2 +y 2 − x2 +y2 0
−x − y + 2x2
2 2
x2 + y 2 − 2y 2
= 0i + 0j + [ − ]k
(x2 + y 2 )2 (x2 + y 2 )2
→
−
= 0
→
− →
− →
−
es decir, F es irrotacional. Por lo tanto, si × F = 0 (que quiere decir
tambi´n que es un campo vectorial conservativo) entonces existe una funci´n
e o
escalar φ tal que :
−
→
F = φ
luego entonces, sustituyendo este resultado en la integral de l´
ınea obtenemos
(1,0) (1,0)
→ →
− −
F ·dr = φ · d→
−
r
(−1,0) (−1,0)
(1,0)
∂φ ∂φ ∂φ
= dx + dy + dz
∂x ∂y ∂z
(−1,0)
(1,0)
= dφ
(−1,0)
el resultado anterior muestra que la integral de l´
ınea depende solamente de los
puntos inicial y final de la trayectoria. Luego entonces, para el inciso b) donde
la trayectoria de integraci´n es la trayectoria poligonal que se muestra en la
o
figura, se obtiene el siguiente resultado
(1,0)
→ →
− − → →
− − → →
− − → →
− −
F ·dr = F ·dr + F ·dr + F · d r = π.
C1 C2 C3
(−1,0)
140

141. Problema 8.
→
−
Demostrar que f = xy 2 i + x3 y j no es conservativo sin aplicar el resultado
→ →
− −
del irrotacional, es decir sin aplicar que × f = 0 .
Soluci´n:
o
→
−
Para mostrar que f no es conservativo, calculamos la integral de l´ ınea del
→
−
campo vectorial f por ejemplo, del punto (0, 0) al punto (1, 0) a lo largo de dos
trayectorias diferentes C1 y C2 como se ilustra en la siguiente figura.
Y
(0,1)
b
a
X
C1 (1,0)
Para C1 :
Las ecuaciones param´tricas de la curva est´n dadas por:
e a
x = x
y = 0
donde 0 ≤ x ≤ 1. Por lo tanto,
→(x) =
−
r xi,
→(x) =
−
dr dxi,
por lo tanto para el campo vectorial dado, obtenemos
(1,0) 1
→ →
− − → →
− −
f ·dr = f ·dr = (0i + 0j) · dxi = 0.
C1
(0,0) x=0
Para C2 , se tiene que
→ →
− − → →
− − → →
− −
f ·dr = f ·dr + f ·dr
C2 a b
141

142. para la trayectoria a; las ecuaciones param´tricas son:
e
x = 0
y = y
donde 0 ≤ y ≤ 1, de donde se obtiene
→(y) =
−
r yj
→(y) =
−
dr dy j
para la trayectoria b, la ecuaci´n param´trica de la recta est´ dada por:
o e a
→(t) = (0, 1) + t(1, −1)
−
r
= ti + (1 − t)j
donde 0 ≤ t ≤ 1,es decir las ecuaciones param´tricas de la curva son:
e
x = t
y = 1−t
por lo tanto para la trayectoria C2 tenemos:
1 1
→ →
− −
f ·dr = (0i + 0j)dy j + t 1 − 2t + t2 − t3 (1 − t) dt
C2
y=0 t=0
1
= [t(1 − 2t + t2 ) − t3 + t4 ]dt
0
1
1 2 1 6 − 20 + 25
= (t4 − 2t2 + t)dt = − + =
0 5 3 2 30
finalmente obtenemos,
→ · d→ = 1 .
− −
r r
c2 30
Por lo tanto, de los resultados anteriores, la integral de l´
ınea s´ depende de la
ı
→
−
trayectoria de integraci´n, luego entonces, el campo vectorial f no es conser-
o
vativo.
Soluci´n alternativa:.
o
→
− →
− →
−
Supongamos que f es conservativo, por lo tanto si × f = 0 entonces
→
−
existe una funci´n escalar φ tal que f = φ es decir;
o
∂φ
= xy 2
∂x
∂φ
= x3 y,
∂y
142

143. pero esto no puede ser, porque de las ecuaciones anteriores obtenemos:
∂ ∂φ
= 2xy
∂y ∂x
∂ ∂φ
= 3x2 y
∂x ∂y
es decir;
∂2φ ∂2φ
=
∂x∂y ∂y∂x
que contradice el resultado fundamental del C´lculo Diferencial que establece
a
que :
∂2φ ∂2φ
= .
∂x∂y ∂y∂x
→
−
Por lo tanto, la hip´tesis original ( f es conservativo) no es correcta, as´ el
o ı
→
−
campo vectorial f no es conservativo.
143

144. Problema 9.
→
−
Calcular el trabajo realizado por un campo de fuerzas F dado por
→
−
F (x, y, z) = (y + 2x)i + (5y − x)j,
x2 y2
que actua sobre una part´
ıcula que se mueve sobre la elipse a2 + b2 = 1, en
sentido opuesto a las manecillas del reloj como se ilustra en la siguiente figura.
fhFU3.5258in2.4327in0ptTrayectoria de integraci´n.dibujoelipse.bmp
o
Soluci´n:
o
→
−
Como el trabajo realizado por el campo de fuerzas F est´ definido por:
a
→ →
− −
W = F ·dr,
C
se puede calcular la integral de l´
ınea tomando la parametrizaci´n
o
x = a cos φ
y = b sin φ
donde 0 ≤ φ ≤ 2π. Sin embargo aplicaremos el teorema de Green, en este caso
si
M (x, y) = y + 2x
N (x, y) = 5y − x,
entonces
∂N
= −1
∂x
∂M
= 1,
∂y
por lo tanto,
144

145. → →
− − ∂N ∂M
F ·d r = − dxdy = [(−1) − 1] dxdy = −2 dxdy = −2A,
∂x ∂y
C Rxy Rxy Rxy
x2 y2
donde A es el area de la elipse
´ a2 + b2 = 1 que es igual πab.
→
−
Por lo tanto el trabajo realizado por el campo de fuerzas F est´ dado por:
a
→ →
− −
W = F · d r = −2πab.
C
145

146. Problema 10.
→
−
a) Verificar si f = 3x2 y i + (x3 + 1)j + 9z 2 k es conservativo.
b) Dependiendo de su respuesta en el inciso anterior calcule la integral de
→
−
l´
ınea de f desde el punto (−1, 0, 2) hasta el punto (1, 2, 4).
Soluci´n:
o
→
−
a) Para verificar que f = 3x2 y i+(x3 +1)j+9z 2 k es conservativo, calculemos
→
−
el rotacional del campo vectorial f .
i j k
→
− ∂ ∂ ∂
× f = ∂x ∂y ∂z
2 3 2
3x y x + 1 9z
= (0 − 0)i − (0 − 0) j + 3x2 − 3x2 k
→
−
= 0.
→
−
Por lo tanto, el campo vectorial f es conservativo.
→ →
− − →
−
b) Si × f = 0 , entonces existe una funci´n escalar talque f =
o φ, es
decir;
∂φ ∂φ ∂φ
3x2 y i + (x3 + 1)j + 9z 2 = i+ j+ k,
∂x ∂y ∂z
de donde obtenemos,
∂φ
= 3x2 y,
∂x
∂φ
= (x3 + 1),
∂y
∂φ
= 9z 2 ,
∂z
integrando parcialmente,
1) φ(x, y, z) = x3 y + f (y, z),
2) φ(x, y, z) = x3 y + y + g(x, z),
146

147. 3) φ(x, y, z) = 3z 3 + h(x, y),
derivando parcialmente con respecto a la variable y, de las ecuaciones 1) y 2)
obtenemos,
∂φ ∂f (y, z)
= x3 + ,
∂y ∂y
∂φ
= x3 + 1,
∂y
de las ecuaciones anteriores obtenemos
∂f (y, z)
= 1,
∂y
integrando nuevamente parcialmente con respecto a la variable y, obtenemos
f (y, z) = y + Ψ(z),
sustituyendo en la ecuaci´n 1) obtenemos,
o
4) φ(x, y, z) = x3 y + y + Ψ(z).
Aplicando nuevamente el mismo procedimiento, es decir; de las ecuaciones
3) y 4), derivamos parcialmente ahora con respecto a la variable z y obtenemos,
∂φ
= 9z 2
∂z
∂φ Ψ(z)
=
∂z ∂z
igualando las ecuaciones enteriores obtenemos,
Ψ(z) = 3z 2 + cte,
→
−
finalmente la funci´n escalar φ(x, y, z) tal que f =
o φ est´ dada por,
a
147

148. φ(x, y, z) = x3 y + y + 3z 2 + cte.
Por lo tanto, aplicando el teorema de campos conservativos
(1,2,4) (1,2,4)
→ →
− −
f ·dr = φ · d→ =
−
r dφ(x, y, z)
C (−1,0,2) (−1,0,2)
= φ(1, 2, 4) − φ(−1, 0, 2)
= 52 − 48 = 4.
148

149. Problema 11.
Calcular el area de una superficie esf´rica.
´ e
Soluci´n:
o
La ecuaci´n de una superficie S se puede representar mediante una funci´n
o o
vectorial de la forma :
→(u, v) = x(u, v)i + y(u, v)j + z(u, v)k,
−
r
donde u y v son par´metros. Asimismo, los elementos diferenciables de l´
a ınea
tangentes a las l´
ıneas coordenadas u y v est´n dadas por:
a
∂→
−
r → du,
−
du = ru
∂u
∂→
−
r → dv,
−
dv = rv
∂v
→
−
de donde, se define el elemento diferencial de superficie d S como:
→ −
−
d S = →u du × →v dv
r −
r
(1) → × → dudv,
− −
= ru rv
y su magnitud est´ dado por:
a
→
−
(2) dS = d S = |→u × →v | dudv.
−
r −
r
Recordemos tambi´n que →u × →v es un vector normal en cada punto de la
e −r −r
superficie S definida por r −
→(u, v), as´ de las ecuaciones anteriores, el elemento
ı
diferencial de superficie est´ dado por :
a
→
−
d S = ndS,
donde n es un vector unitario normal en cada punto de la superficie S y est´
a
dado por:
149

150. → ×→
−
ru −v
r
n= →− × → |.
|ru −v
r
De la ecuaci´n (2), integrando la magnitud del elemento diferencial dS,
o
sobre toda la superficie de la esfera se puede obtener el area de la superficie S
´
es decir:
→
− →
−
S= dS = n · dS .
S S
Como sabemos, para una superficie esf´rica la forma param´trica para la
e e
superficie est´ dada por:
a
→(θ, φ) = a sin θ cos φi + a sin θ sin φj + a cos θ k,
−
r
donde, 0 ≤ θ ≤ π y 0 ≤ φ ≤ 2π. Por lo tanto, los vectores tangentes a las
l´
ıneas coordenadas θ y φ est´n dados por,
a
→
−
→ ≡ ∂ r = a cos θ cos φi + a cos θ sin φj + a sin θ k
−
rθ
∂θ
y
→
−
→ ≡ ∂ r = a sin θ sin φi + a sin θ cos φj
−
rφ
∂φ
por lo tanto,
i j k
→ ×→
−
rθ −φ
r = a cos θ cos φ a cos θ sin φ a sin θ
a sin θ sin φ a sin θ cos φ 0
= a2 sin2 θ cos φi + a2 sin2 θ sin φj + a2 sin θ cos θ(cos2 φ + sin2 φ)k
= a2 sin2 θ cos φi + a2 sin2 θ sin jφj + a2 sin θ cos θ k,
de lo anteriormente aplicando la ecuaci´n (2), la magnitud del elemento de
o
superficie para este caso est´ dado por:
a
→
−
dS = d S = |→θ × →φ | dθdφ,
−
r −
r
150

151. donde,
|→θ × →φ | =
−
r −
r 2
a4 sin4 θ cos2 φ + sin2 φ + sin2 θ cos2 θ
= 2
a4 sin2 θ sin2 θ + cos2 θ
= a2 sin θ,
por lo tanto, el area de una superficie esf´rica est´ dado por:
´ e a
2π π 2π π
2 2
S = dS = a sin θdθdφ = a dφ sin θdθ = a2 (φ 2π π
0 )(cos θ 0 )
S φ=0 θ=0 φ=0 θ=0
2
= −a (2π) [(cos (π) − cos (0)]
= 4πa2 .
151

152. Problema 12.
→
−
Calcular d S donde S es la parte z > 0 de una esfera.
S
Soluci´n:
o
Para el caso de una superficie esf´rica donde z > 0, la ecuaci´n param´trica
e o e
de dicha superficie est´ dada por :
a
→(θ, φ) = a sin θ cos φi + a sin θ sin φj + a cos θ k,
−
r
donde;
0 ≤ θ ≤ π/2,
0 ≤ φ ≤ 2π.
En este caso, la integral de superficie resulta
π
→
− 2π 2
1) dS = (→θ × →φ ) dθdφ
−
r −
r
S φ=0 θ=0
del ejemplo anterior un vector normal a la superficie de la esfera est´ dado por:
a
→ × → = a2 sin2 θ cos φi + a2 sin2 θ sin φj + a2 sin θ cos θ k,
−
rθ −φ
r
sustituyendo en la integral de superficie obtenemos,
π
2π 2
−
→
dS = a2 sin2 θ cos φi + sin2 θ sin jφj + sin θ cos θ k dθdφ
S φ=0 θ=0
π π
2π 2 2π 2
= a2 sin2 θ cos φdθdφi + a2 sin2 θ sin φdθdφj +
φ=0 θ=0 φ=0 θ=0
π
2π 2
2
a sin θ cos θdθdφk,
φ=0 θ=0
152

153. las integrales de las componentes i y j se pueden separar de la forma,
π π
2π 2 2π 2
a2 sin2 θ cos φdθdφ = a2 cos φdφ sin2 θdθ
φ=0 θ=0 φ=0 θ=0
π π
2π 2 2π 2
a2 sin2 θ sin φdθdφ = a2 sin φdφ sin2 θdθ,
φ=0 θ=0 φ=0 θ=0
pero
2π 2π
cos φdφ = sin φdφ = 0.
φ=0 φ=0
Por lo tanto la integral de superficie resulta ser,
π
2π 2
→
−
dS = a2 dφ sin θ cos θdθ k
S φ=0 θ=0
π
2 sin2 θ 2
= 2a π
2 0
1 π
= 2a2 π sin2 − sin2 (0) ,
2 2
finalmente obtenemos,
→
−
2) d S = πa2 k.
S
153

154. Problema 13.
→
−
Calcular d S donde S es una esfera.
S
Soluci´n:
o
La integral original se puede escribir como:
→
− →
− →
−
dS = dS + dS ,
S S1 S2
donde S1 es la parte de la esfera z ≥ 0 y S2 es la parte de la esfera z ≤ 0. As´
ı
del problema anterior usando la ecuaci´n 2) se tiene,
o
→
−
d S = πa2 k.
S1
An´logamente, para la parte de la esfera z ≤ 0 aplicando la ecuaci´n 1) del
a o
problema anterior obtenemos,
→
−
dS = (→θ × →φ ) dθdφ
−
r −
r
S2 S2
2π π
2
= a sin θ cos θdθdφk
φ=0 θ= π
2
2π π
2
= a dφ sin θ cos θdθdφk
φ=0 θ= π
2
1 π
= a2 [2π] sin2 (π) − sin2 k
2 2
= −πa2 k,
finalmente obtenemos,
→ →
− −
dS = 0 .
S
154

155. Problema 14:
→
− → →
− −
Sea E = −grad 1
donde → = xi + y j + z k. Calcular
−
r E · d S , donde
|→|
−r S
S es la esfera x2 + y 2 + z 2 = 9.
Soluci´n:
o
Por definici´n si φ = φ(r), donde r = |→| entonces, el gradiente est´ dado
o −
r a
por la expresi´n,
o
→
−
r
φ(r) = φ (r) → ,
−|
|r
1
en este caso tenemos que la funci´n dada es igual a φ(r) =
o , por lo tanto el
|→|
−
r
→
−
campo vectorial E est´ dado por:
a
→
− 1 →
−
E =− =− | →|
−
r
−1 − −2 r
= − − |→|
r ,
|→ |
−
r |−
→|
r
es decir,
→
− →
−
r
E = → 3.
−|
|r
→
−
Por otro lado, el elemento diferencial de superficie d S est´ dado por:
a
→
−
d S = ndS,
donde el vector n, es un vector unitario normal a la superficie, que en este caso
es una esfera, y aplicando la propiedad que establece que el gradiente es normal
o perpendicular a una superficie, este vector esta dado por:
φ(x, y, z) x2 + y 2 + z 2 2xi + 2y j + 2z k xi + y j + z k
n= = = = ,
| φ(x, y, z)| | (x2 + y 2 + z 2 )| 2xi + 2y j + 2z k x2 + y 2 + z 2
es decir,
155

156. →
−
r
n= → ,
−|
|r
este resultado se pudo haber obtenido inmediatamente aplicando el resultado
de que φ = φ(r), donde r = |→| , tomando φ(r) = r 2 .
−
r
→
−
Por lo tanto sustituyendo el resutado para el campo vectorial E y el resul-
→
−
tado para el vector d S , la integral de superficie resulta ser,
→ →
− − →
−r →
−
r
E · dS = 3 · |→| dS
−
S S |→|
−r r
1
= − 2 dS
|→| S
r
donde, de la ecuaci´n para la esfera x2 + y 2 + z 2 = 9, se tiene que |→| =
o − 2
r
x2 + y 2 + z 2 = 9. Finalmente apicando el resultado del problema 11, la integral
est´ dada por:
a
→ → 1
− − 2
E · dS = 4π (3) = 4π.
S 9
156

157. Problema 15.
Calcular
dS
S 1 ,
[a2 x2 + b2 y 2 + c2 z 2 ] 2
sobre la superficie del elipsoide dada por la ecuaci´n ax 2 + by 2 + cz 2 = 1.
o
Soluci´n:
o
La integral de superficie se puede calcular en forma param´trica de la forma,
e
∂→ ∂→
−
r −
r
S f dS =T f (→ (u, v))
−
r × dudv,
∂u av
analizando la ecuaci´n del elipsoide, una parametrizaci´n para la superficie S,
o o
est´ dada por las ecuaciones param´tricas,
a e
1
x = √ sin θ cos φ,
a
1
y = √ sin θ sin φ,
b
1
z = √ cos θ,
c
as´ la ecuaci´n del elipsoide en forma param´trica est´ dada por,
ı, o e a
1 1 1
→ (θ, φ) = √ sin θ cos φi + √ sin θ sin φj + √ cos θ k,
−r
a b c
por lo tanto, los vectores tangentes a las l´
ıneas coordenadas θ y φ est´n dados
a
por,
∂→
−
r 1 1 1
= √ cos θ cos φi + √ cos θ sin φj − √ sin θ k
∂θ a b c
∂→
−
r 1 1
= √ sin θ sin φi + √ sin θ cos φj
∂φ a b
de esta forma, el vector normal a la superficie est´ dado por,
a
i j k
∂→ ∂→
−
r −
r 1 1 1
× = √ cos θ cos φ
a
√
b
cos θ sin φ − √c sin θ
∂θ ∂φ 1 1
− √a sin θ sin φ, √
b
sin θ cos φ 0
1 1 1 1
= sin θ √ sin θ cos φi − √ sin θ sin φj + √ cos2 φ cos θ + √ cos θ sin2 φ k
bc ac ab ab
1 1 1
= sin θ √ sin θ cos φi − √ sin θ sin φj + √ cos θ k. ,
bc ac ab
157

158. y la magnitud est´ dada por,
a
∂→ ∂→
−
r −
r a sin2 θ cos2 φ b sin2 θ sin2 φ c cos2 θ
× = sin θ + +
∂θ ∂φ abc abc abc
sin θ
= √ a sin2 θ cos2 φ + b sin2 θ sin2 φ + c cos2 θ
abc
as´ tambi´n, en t´rminos de las ecuaciones param´tricas, la funci´n escalar f se
ı e e e o
puede escribir de la froma,
1
f (→ (θ, φ)) =
−
r 1
a sin2 θ cos2 φ + b sin2 θ sin2 φ + c cos2 θ 2
por lo tanto, la integral de superficie est´ dada por:
a
1
sin θ a sin2 θ cos2 φ + b sin2 θ sin2 φ + c cos2 θ 2
S f dS =T √ 1 dθdφ,
abc a sin2 θ cos2 φ + b sin2 θ sin2 φ + c cos2 θ 2
que se reduce simplemente a la forma,
2π π
1 1
S f dS = √ sin θdθdφ = √ dφ sin θdθ
abc T abc φ=0 φ=0
π
2π 2π π
= √ sin θdθ = √ [(− cos θ)0 ]
abc θ=0 abc
2π
= √ [− (cos π − cos 0)]
abc
finalmente se obtiene,
dS 4π
S 1 =√ .
[a2 x2 + b2 y 2 + c2 z 2 ] 2 abc
158

159. Problema 16.
→ →
− − →
−
Calcular f ·d S donde f = x2 i+xy j −xz k y S la superficie del plano que
S
contiene a los puntos (1, 0, 0), (0, 2, 0) y (0, 0, 3) limitado en el primer octante.
Soluci´n:
o
Primero debemos escribir la ecuaci´n de la superficie S de la forma,
o
ax + by + cz = d,
→
−
donde N = (a, b, c) ser´ un vector normal al plano que contiene a los tres
a
puntos dados. Sean los puntos P, Q y R que est´n en el plano con sus
a
respectivos vectores de posici´n →P , →Q y →R , en t´rminos de estos vectores de
o − −
r r −r e
posici´n podemos encontrar dos vectores sobre el plano y calculando su producto
o
vectorial entre ellos podemos encontrar un vector perpendicular a ambos y por
lo tanto perpendicular al plano, de la forma
→
−
N = (→P − → Q ) × ( →R − → Q )
−r −r −
r −
r
= (1, −2, 0) × (0, −2, 3)
i j k
= 1 −2 0
0 −2 3
= −6i − 3j − 2k,
adem´s,
a
→ −
−
d = N · →P = (−6, −3, −2) · (1, 0, 0) = −6.
r
Por lo tanto, la ecuaci´n del plano que contiene a los puntos (1, 0, 0), (0, 2, 0)
o
y (0, 0, 3) est´ dado por:
a
−6x − 3y − 2z = −6,
que se puede escribir de la forma,
1 1
x + y + z = 1.
2 3
La superficie de integraci´n esta representada en la siguiente figura.
o
159

160. (0,0,3) Z
plano x=0
i,e; plano YZ
plano y=0
i,e; plano XZ
3y + 2z = 6
6x + 2z = 6
Y
(0,2,0)
(1,0,0)
plano z=0
i,e; plano XY
X 6x + 3y = 6
Por lo tanto, aplicando el teorema de la proyecci´n de la superficie en el
o
plano coordenado rect´ngular XY, la integral de superficie est´ dada por:
a a
→
−
→
− f ·n
f · ndS = dxdy,
S Rxy
n·k
donde el vector unitario normal al plano est´ dado por:
a
160

161. φ i + 1j + 1k
2 3
n = =
| φ| 1
1+ 4 + 9 1
i + 1j + 1k
2 3
7
6
de donde obtenemos,
→
− 1 1 6
f ·n = x2 i + xy j + xz k · i + j + k
2 3 7
n·k = ()13()67,
as´ al sustitur en la integral de superficie obtenemos,
ı,
→
−
f ·n x2 + xy + xz
2 3
6
7
dxdy = dxdy
n·k ()13()67
Rxy Rxy
xy xz
= 3 x2 + + dxdy
2 3
Rxy
y
pero de la ecuaci´n del plano tenemos que z = 3 1 − x −
o 2 , sustituyendo en
la ecuaci´n anterior tenemos,
o
→
−
f ·n xy y
dxdy = 3 x2 + +x 1−x− dxdy
n·k 2 2
Rxy Rxy
= 3 xdxdy,
Rxy
para resolver la integral enterior, observemos la regi´n en el plano XY , el orden
o
de integraci´n se muestra esquem´ticamente en la figura siguiente.
o a
161

162. Y
(0,2)
X
(1,0)
Mantenemos fijo a y e integramos con respecto a x desde x = 0 hasta la
recta x = 1 − 1 y; finalmente integramos y desde y = 0 hasta y = 2, es decir;
2
 
2 x=1− 1 y
2 2
  x2 (1− y )
3 xdxdy = 3  xdx dy = 3 |0 2 dy
2
Rxy y=0 x=0 y=0
2 2
y 3
3 y 2 −3 1 − 2 3
= 1− dy = =+ = 1.
2 2 3 3
y=0 0
Tambi´n como se muestra esquem´ticamente en la figura, podemos resolver
e a
la integral en el siguiente orden de integraci´n, manteniendo fijo a x e integrando
o
con respecto a y desde y = 0 hasta la recta y = 2(1 − x), finalmente integramos
con respecto a x desde x = 0 hasta x = 1, es decir;
162

163. Y
(0,2)
6X + 3Y = 6
X
(1,0)
 
1 y=2(1−x) 1
  2(1−x)
3 xdxdy =  xdy  dx = 3 (xy) |0 dx
Rxy x=0 y=0 x=0
1 1
x2 x3 1 1
= 3 x(1 − x)dx = 6 − =6 − = 1.
2 3 0 2 3
x=0
Los resultados anteriores muestran que el resultado de una integral doble es
independiente del orden de integraci´n.
o
163

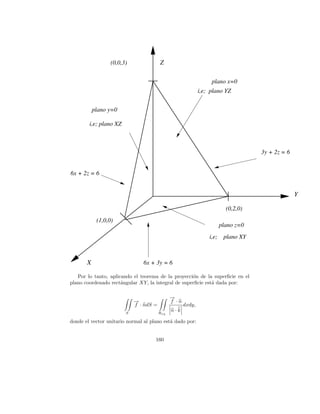
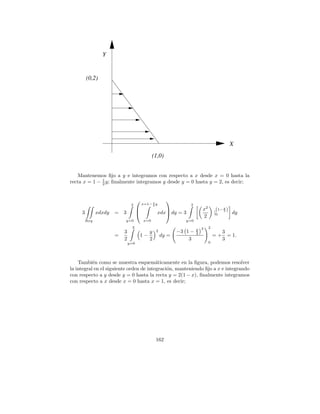
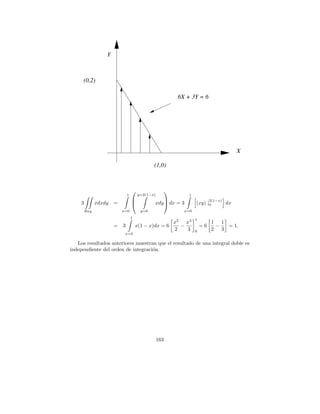
164. Problema 17.
→ →
− − →
−
Calcular la integral f ·d S para f = y i+2xj −z k, donde S es la superficie
S
del plano 2x + y + 2z = 6 situado en el primer octante.
Soluci´n:
o
Aplicando el gradiente, un vector normal unitario a la superficie S, que en
este caso es un plano, est´ dado por,
a
φ 2i + j + 2 k
n= = ,
| φ| 3
de donde:
→
− 1
f ·n = [2y + 2x − 2z] ,
3
2
n·k = ,
3
por lo tanto,
→
− 1
f ·n 3 (2x + 2y − 2z)
dxdy = 2 dxdy,
Rxy
n·k Rxy
3
1
pero de la expresi´n para la superficie tenemos z = 3 − x − 2 y, sustituyendo en
o
la integral anterior obtenemos
→
−
f ·n 1
dxdy = x + y − (3 − x − y) dxdy
n·k 2
Rxy Rxy
3
= 2x + y − 3 dxdy.
2
Rxy
Despu´s de algunos c´lculos algebraicos an´logos al problema anterior obten-
e a a
emos,
→
−
f ·n
dxdy = 18.
Rxy
n·k
164

165. Problema 18.
→
−
Calcular el flujo de campo f = xi + y j + z k donde S es un cubo unitario
(es decir la superficie limitada por los planos x = 0, y = 0, z = 0, x = 1, y = 1,
z = 1).
Soluci´n:
o
Como se muestra en la figura, el flujo a trav´s del cubo tiene 6 contribu-
e
ciones debidas a las 6 superficies (caras) del cubo unitario, es decir los planos
(x = 0, y = 0, z = 0, x = 1, y = 1, z = 1) , por lo tanto la integral de flujo
original est´ dada por:
a
→ →
− − → →
− − → →
− − → →
− − → →
− −
f · dS = f · dS + f · dS + f · dS + ···+ f · dS
S S1 S2 S3 S6
donde, como se muestra en la figura tenemos
→
−
S1 (DEF G) ; x = 1 d S = ndS = idydz
→
−
S2 (ABCO) ; x = 0 d S = ndS = −idydz
→
−
S3 (ABEF ) ; y = 1 d S = ndS = jdxdz
→
−
S4 (0GDC) ; y = 0 d S = ndS = −jdxdz
→
−
S5 (BCDE) ; z = 1 d S = ndS = kdxdy
→
−
S6 (AF GO) ; z = 0 d S = ndS = −kdxdy.
165

166. Z
C
B
E
D
O
Y
A
G
F
X
Por lo tanto, para la superficie S1 tenemos,
→ →
− −
f ·ds = (xi + y j + z k) · idydz
s1 Rxy
1 1 1 1
= xdydz = dydz = 1,
y=0 z=0 y=0 z=0
an´logamente para la superficie S2 tenemos,
a
166

167. → →
− −
f ·ds = (xi + y j + z k) · −idydz
s2 Rxy
= − xdydz = 0.
Rxy
Similarmente para las superficies S3 , S4 , S5 y S6 obtenemos;
→ →
− − → →
− −
f · dS = f · d S = 1,
S3 S5
→ →
− − → →
− −
f · dS = f · d S = 0,
S4 S6
por lo tanto el flujo a trav´s del cubo unitario est´ dado por:
e a
→ →
− − → →
− − → →
− − → →
− − → →
− −
f ·dS = f ·dS + f ·dS + f ·dS +···+ f · d S = 3.
S S1 S2 S3 S6
El resultado anterior se puede obtener aplicando el teorema de Gauss, este
teorema establece lo siguiente:
→ →
− − →
−
f ·ds = · f dV
s V
en este caso:
→ →
−
f =−,
r
por lo tanto,
→
−
· f dV = 3 dV = 3,
V V
donde dV es el volumen de un cubo unitario.
V
167

168. Problema 19.
→
−
Calcule el flujo del campo vectorial F = i + xy j a lo largo de la superficie
S dada por las ecuaciones param´tricas:
e
x = u + v,
y = u − v,
z = u2 ,
donde,
0 u 1
0 v 1.
Soluci´n:
o
→
−
El flujo del campo vectorial F a trav´s de la superficie S (que generalmente
e
se representa por Φ) esta dado por:
→ −
− →
Φ= F · dS,
S
donde
→
−
d S = ndS,
y
→ ×→
−
ru −v
r
n= →− × → |,
|ru −v
r
es un vector normal unitario en cada punto de la superficie S dada por la
ecuaci´n,
o
→ = →(u, v),
−
r −
r
donde los vectores →u y →v , son vectores tangentes a las l´
−
r −
r ıneas coordenadas u y
v respectivamente. Asimismo, la magnitud del elemento diferencial de superficie
est´ dada por,
a
dS = |→u × →v | dudv
−
r −
r
168

169. por lo tanto,
→
− → ×→
−
ru −v →
r − →
−
dS = → × → | | r u × r v | dudv
−
|ru −
rv
∂→ ∂→
−r −r
= × dudv,
∂u ∂v
que es el elemento diferencial de area normal a la superficie S. De las ecuaciones
´
param´trica para la superficie S, elvector de posici´n se puede escribir de la
e o
forma,
→(u, v) = (u + v)i + (u − v)j + u2 k,
−
r
calculando el vector normal a la superficie, obtenemos
∂→
−
r
= i + j + 2uk,
∂u
∂→
−
r
= i − j,
∂v
de donde obtenemos,
∂→ ∂→
−
r −
r i j k
× = 1 1 2u = 2ui + 2uj − 2k,
∂u ∂v
1 −1 0
→
−
por lo tanto, el flujo del campo vectorial F a trav´s de la superficie S est´ dado
e a
por,
→ −
− →
F · dS = i + (u + v)(u − v)j · 2ui + 2uj − 2k dudv,
S S
calculando el producto escalar,
169

170. v=1 u=1
→ −
− →
F · dS = 2u + 2u(u2 − v 2 ) dudv
v=0 u=0
S
1 1
= (2u3 − 2uv 2 + 2u)dudv
v=0 u=0
1 1
2 4
= u − u2 v 2 + u2
v=0 4 u=0
1
1
= − v 2 + 1) dv
u=0 2
1 1
2 3 v3
= − v 2 dv = v− ,
u=0 3 2 3 0
finalmente, obtenemos
→ −
− → 7
F · dS = .
6
S
170

171. Problema 20.
→
− → →
− −
Si f = xi + y j + z k Calcualr s f · d S , donde S es la superficie cil´
ındrica
representada por la ecuaci´n
o
→ = cos ui + sin uj + v k.
−
r
donde,
0 ≤ u ≤ 2π,
0 ≤ v ≤ 1,
→
−
y el elemento diferencial est´ dado por d S = ndS, y n es el vector unitario
a
normal exterior a la superficie.
Soluci´n:
o
Por definici´n, sabemos que el vector
o
→ ×→
−
ru −v
r
n= →− × → |,
−
|ru rv
es un vector normal unitario en cada punto de la superficie S dada por la
ecuaci´n,
o
→ = →(u, v)
−
r −
r
los vectores →u y →v , son vectores tangentes a las l´
−
r −
r ıneas coordenadas u y v
respectivamente. Por otro lado, si el elemento diferencial de superficie est´ dado
a
por
→
−
d S = ndS,
y su magnitud est´ dada por,
a
dS = |→u × →v | dudv
−
r −
r
entonces,
→
− → ×→
−
ru −v →
r − →
−
dS = → × → | | r u × r v | dudv
−
|ru −
rv
= → × → dudv
−
r −
r
u v
171

172. Para la ecuaci´n de la superficie dada, los vectores tangentes a las l´
o ıneas
coordenada est´n dados por,
a
→
− ∂→
−
r
ru = = − sin ui + cos uj,
∂u
→
−
∂r
→
−
rv = = k,
∂u
de donde,
i j k
→ ×→ =
−
ru −v
r − sin u cos u 0 = cos ui + sin uj,
0 0 1
por otro lado, de las ecuaciones param´tricas de la superficie cil´
e ındrica, el campo
vectorial est´ dado por
a
→
−
f = cos ui + sin uj + v k ,
por lo tanto, la integral de flujo resulta
v=1 u=2π
→ →
− −
s f · dS = cos ui + sin uj + v k · cos ui + sin uj dudv
v=0 v=0
v=1 u=2π
= cos2 u + sin2 v dudv
v=0 v=0
v=1 u=2π
= dudv
v=0 v=0
v=1 u=2π
= dv du
v=0 v=0
= 2π.
172

173. Problema 21.
→ −
−
Calcular c f · d→ donde C es la trayectoria cerrada que se muestra en la
r
→
−
figura y el campo vectorial est´ dado por: f = (x − y) i + (x + y) j
a
a) Calculando la integral de l´
ınea directamente y
b) Aplicando el Teorema de Green en el plano
Y
(1,1)
y=x
2
y=x
X
Soluci´n:
o
a) De la figura, la trayectoria curva C se divide en dos trayectorias C 1
y = x2 y C2 (y = x) , por lo tanto, la integral de l´
ınea se expresa de la forma:
→ →
− − → →
− − → →
− −
f ·dr = f ·dr + f ·dr
C C1 C2
Para la trayectoria C1 las ecuaciones param´tricas est´n dadas por:
e a
x = x
y = x2 ,
de donde, el elemento diferencial de l´
ınea est´ dado por:
a
d→ = dxi + 2xdxj,
−
r
por lo tanto, la integral de l´
ınea para la trayectoria C 1 est´ dada por:
a
173

174. 1
→ →
− −
f ·dr = (x − x2 )dx + x + x2 2xdx
C1
x=0
1 1
x2 x3 x4
= x + x2 + 2x3 dx = + +
2 3 2 0
0
1 1 1 1 3 4
= + + = + = .
2 3 2 3 3 3
Asimismo para la trayectoria C2 las ecuaciones param´tricas est´n dadas
e a
por:
x = x
y = x,
de donde, el elemento diferencial de l´
ınea est´ dado por:
a
d→ = dxi + dxj,
−
r
por lo tanto la integral de l´
ınea para la trayectoria C 2 est´ dada por:
a
0
→ →
− −
f ·dr = (x − x) dx + 2xdx
c2
1
0 3
= x2 1
= −1 = − .
3
Por lo tanto la integral de l´
ınea a lo largo de la trayectoria C que se muestra
en la figura est´ dado por:
a
→ →
− − → →
− − → → 4 3
− − 1
f ·dr = f ·dr + f ·dr = − =
C C1 C2 3 3 3
b) En este caso
M (x, y) = x−y
N (x, y) = x + y,
de donde se tiene,
∂N
= 1
∂x
∂M
= −1,
∂y
174

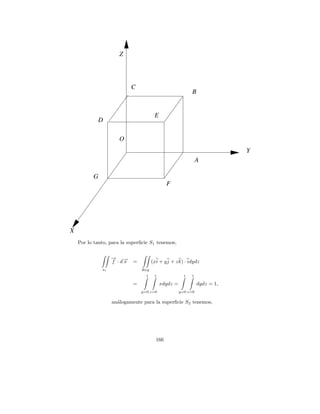
175. aplicando el teorema de Green en el plano, obtenemos
∂N ∂M
(M dx + N dy) = − dxdy
C ∂x ∂y
Rxy
= (1 − (−1)) dxdy = 2 dxdy,
Rxy Rxy
para evaluar la integral doble hacemos uso de la figura, integrando primeramente
desde la recta y = x a la par´bola y = x2 para despu´s integrar la variable y
a e
desde y = 0 hasta y = 1, es decir;
√
1 x= y 1
√
y
2 dxdy = 2 dxdy = 2 [x]y dy
Rxy y=0 x=y y=0
1
√ 1
= 2 ( y − y) dy = .
3
y=0
La integral doble tambi´n se puede resolver integrando primeramente en la
e
variable y, posteriormente la variable x de la siguiente forma,
1 y=x 1
x
2 dydx = dydx = 2 ([y]x2 ) dx
Rxy x=0 y=x2 x=0
1 1
2 x2 x3 1
= 2 x−x dx = 2 − = .
2 3 0 3
0
175

176. Problema 22:
Verificar el Teorema de Green en el plano para el campo vectorial,
→
−
F = 3x2 + 2y i − (x + 3 cos y) j
donde C es la trayectoria que se muestra en la siguiente figura.
ftbpF206.4375pt130.125pt0ptFigure
Soluci´n:
o
Debemos verificar que,
∂N ∂M
M dx + N dy = − dxdy,
C Rxy ∂x ∂y
en este caso;
M = 3x2 + 2y ,
(∗)
N = − (x + 3 cos y) .
Primero calculemos la integral de l´
ınea a lo largo de las cuatro trayectorias
rectas que se muestran en la figura que es un paralelogramo, para despues sumar
todos los resultados, es decir,
M dx + N dy = + + + .
C C1 C2 C3 C4
Para C1 :
De la figura, la recta que va del punto (0, 0) al punto (2, 0), est´ dada por
a
las ecuaciones param´tricas
e
x = x,
y = 0,
por lo tanto,
(2,0)
x=2
M dx + N dy = x=0 3x2 + 2y dx
(0,0)
2
= x3 + 2y 0
= 8.
Para C2 :
De la figura, la recta que va del punto (2, 0) al punto (3, 1), est´ dada por
a
las ecuaci´n,
o
x = y + 2,
176

177. si escogemos como par´metro a la variable y, obtenemos
a
(3,1)
y=1 2
M dx + N dy = y=0 3 (y + 2) + 2y − (y + 2) − 3 cos y dy
(2,0)
y=1
= y=0 3y 2 + 12y + 12 + 2y + y − 2 − 3 cos y dy
y=1
= y=0 3y 2 + 12y + 10 − 3 cos y dy
1
13 2
= y3 + y + 10y − 3 sin (1)
2 0
13
= 1+ + 10 − 3 sin (1)
2
35
= − 3 sin (1) .
2
Para C3 :
De la figura, la recta que va del punto (3, 1) al punto (1, 1), est´ dada por
a
las ecuaciones param´tricas,
e
x = x,
y = y,
por lo tanto,
(1,1)
M dx + N dy = −x=3 3x2 + 2y dx
x=1
(3,1)
3
= − x3 + 2y 1
= −30.
Para C4 :
De la figura, la recta que va del punto (1, 1) al punto (0, 0), est´ dada por
a
las ecuaci´n,
o
x = y,
si escogemos como par´metro a la variable y, obtenemos
a
(0,0)
M dx + N dy = −y=1 3y 2 + 2y)dy − (y + 3 cos y dy
y=0
(1,1)
1
y2
= − y3 + y2 − − 3 sin (y)
2 0
3
= − + 3 sin (1) ,
2
177

178. sumando los resultados obtenidos para las cuatro trayectorias rectas, obtenemos
35 3
M dx + N dy = 8 + − 3 sin (1) − 30 − + 3 sin (1) ,
C 2 2
de donde,
(1) C
M dx + N dy = −6.
Ahora para calcular la integral doble sobre la regi´n que encierra el paralel-
o
ogramo, tenemos de las ecuaciones (∗) que,
∂N
= −1,
∂x
y
∂M
= 2,
∂y
por lo tanto,
∂N ∂M
− dxdy = (−1 − 2)dxdy = −3y=1
y=0
x=y+2
x=y dx dy
Rxy ∂x ∂y Rxy
x=y+2
= −3y=1 [x]x=y
y=0 dy = −3y=1 2dy,
y=0
finalmente,
∂N ∂M
(2) ∂x − ∂y dxdy = −6.
Rxy
Este resultado se pudo haber obtenido por simple observaci´n, puesto que
o
dxdy es igual al area del paralelogramo que tiene base igual a dos y alura
´
Rxy
uno.
As´ de los resutados (1) y (2), se comprueba el Teorema de Green en el
ı,
plano.
178

179. Problema 23.
Aplique el teorema de Green en el plano para calcular la integral,
(x + y)dx + x2 dy,
C
donde C es el tri´ngulo con v´rtices (0, 0), (2, 0) y (0, 1), que se muestra en la
a e
siguiente figura.
Y
(0,1)
X
(0,0) (2,0)
Soluci´n:
o
Por definici´n, el teorema de Greenn en el plano establece que
o
∂N ∂M
M dx + N dy = ( − )dxdy,
∂x ∂y
C Rxy
donde la trayectoria curva C encierra la regi´n que R xy que est´ en el plano
o a
XY .
En este caso,
M = x + y,
N = x2 ,
de donde se obtiene,
∂N
= 2x,
∂x
∂M
= 1,
∂y
179

180. por lo tanto, aplicando el teorema de Green en el plano, obtenemos
(x + y)dx + x2 dy, = (2x − 1) dxdy,
Rxy
C
para resolver la integral interior, mantenemos fijo a y e integramos con respecto
a x, desde la recta x = 0, hasta la recta x = 2(1 − y), como se muestra en la
siguiente figura, y finalmente integramos y desde y = 0 hasta y = 2.
Y
(0,1)
X
(0,0) (2,0)
de esta forma, obtenemos
1 x=2(1−y)
(x + y)dx + x2 dy = (2x − 1)dxdy,
y=0 x=0
C
calculando las integrales obtenemos
1
x=2(1−y)
(x + y)dx + x2 dy = x2 − x x=0
dy
y=0
C
1
= 4(1 − y)2 − 2(1 − y) dy
y=0
1 1
= 4 (1 − y)2 dy − 2 (1 − y)dy
y=0 y=0
1
4 3 2
= − (1 − y) + (1 − y)
3 y=0
4 3 4 3 2
= − (1 − 1) + (1 − 1)2 − − (1 − 0) + (1 − 0)
3 3
4 6
= − − +
3 3
2
= − .
3
180

181. Problema 24.
Aplique el teorema de Green en el plano para calcular
(y − sin x) dx + cos xdy,
C
donde C es el tri´ngulo que se muestra en la siguiente figura.
a
π,
Y ( 2
0 )
X
( π2 ,0 )
Soluci´n:
o
En en forma an´loga al problema anterior, en este caso
a
M (x, y) = y − sin x
N (x, y) = cos x,
de donde se tiene,
∂N
= − sin x
∂x
∂M
= 1,
∂y
aplicando el teorema de Green en el plano, obtenemos
(y − sin x) dx + cos xdy = (− sin x − 1) dxdy.
C
Rxy
Para evaluar la integral doble, integrando primeramente la variable y, desde
2
la recta y = 0 a la recta y = π x, para despu´s integrar la variable x, desde
e
π
x = 0 hasta x = 2 ,como se esquematiza en la siguiente figura.
Y
(π
2
, )
1
X
π
( 2
, 1 )
181

182. Por lo tanto la integral doble resulta,
 
x= π
2 y= π x
2
 
(− sin x − 1) dydx = −  (sin x + 1) dy  dx
Rxy x=0 y=0
x= π
2
π
x
= − [(sin x)y + y]y=0 dx
2
x=0
 
x= π
2 x= π
2 π
2 2x
π π x= π x 
= − x [sin x + 1] dx = − (−x cos x)x=0 + 2
cos xdx + 
2 2 2 y=0
x=0 x=0
π
2x π 2
2 x2 2 π π π 2
= − −x cos x + sin x + =− − cos + sin +
π 2 y=0 π 2 2 2 2
2 π2 2 π2 + 8
= − 1+ =− ,
π 8 π 4π
finalmente, obtenemos
π 2
(− sin x − 1) dydx = − + .
4 π
Rxy
182

183. Problema 25.
Calcular la integral
→
−
F · ndS,
S
−
→
donde F est´ dado por:
a
→
−
F (x, y, z) = [2x + cos(yz)] i − [sin(xz) + 5y] j + arcsin x2 y k,
y S es la parte superior del plano XY de la esfera x 2 + y 2 + z 2 = a2 .
Soluci´n:
o
Obs´rvese que s´ se quiere calcular directamente la integral de superficie
e ı
resulta ser una integral muy laboriosa, sin embargo si aplicamos el teorema
de la Divergencia de Gauss el problema es relativamente simple, puesto que
→
−
· F = 7, as´ aplicando el teorema de la divergnecia de Gauss obtenemos,
ı
→ →
− − →
−
F · dS = · f dV = 7 dV,
S V V
donde dV es el volumen de la esfera, pero como se pide solamente la parte
V
z > 0, entonces
→ →
− − 2 3 14 3
F · dS = 7 πa = πa .
3 3
S
183

184. Problema 26.
→
−
Verificar el teorema del rotacional de Stokes para F = (x + 2y) i + 3z j + yz k
y S la superficie de la mitad superior de la esfera x 2 + y 2 + z 2 = a2 .
Soluci´n:
o
El teorema del rotacional de Stokes matem´ticamente se expresa de la forma,
a
→ →
− − → →
− −
S × F · dS = F ·dr ,
C
es decir, la integral de superficie de la componente normal del rotacional de un
campo vectorial, tomada sobre una superficie cerrada, es igual a la integral de
l´
ınea de la componente tangencial del campo vectorial, tomada sobre la curva
cerrada que limita o rodea a la superficie. Primero calcularemos la integral de
l´
ınea.
Si proyectamos a la esfera en el plano XY, tenemos una circunferencia de
radio a con centro en el origen cuyas ecuaciones param´tricas est´n dadas por,
e a
x = a cos θ,
y = a sin θ,
z = 0,
donde 0 < θ < 2π. En t´rminos de estas ecuaciones param´tricas, el campo
e e
vectorial est´ dado por
a
→
−
F = (a cos θ + 2a sin θ) i + 0j + 0k.
Asimismo, el vector de posici´n →,est´ dado por,
o −r a
→ = a cos θ i + a sin θ j,
−
r
de donde, el elemento diferencial de l´
ınea est´ dado por,
a
d→ = −a sin θdθ i + a cos θdθ j.
−
r
Calculando la integral de l´
ınea en sentido positivo (como lo establece el
teorema) tenemos,
184

185. 2π
→ →
− −
F ·dr = − (a cos θ + 2a sin θ) i · −a sin θ i + a cos θ j dθ
θ=0
2π 2π
= −a2 cos θ sin θdθ − 2a sin2 θdθ
θ=0 θ=0
2π 2π
sin2 θ 1
= −a2 − a2 θ − sin(2θ)
2 θ=0 2 θ=0
2 sin2 (2π) 1
= −a − a2 2π − sin (2 (2π))
2 2
1
= −a2 2π − sin 2 (2π) = −2a2 π.
2
Ahora, calculemos la integral de superficie, para hacer esto calculamos primer-
→
−
amente el × F ,
i j k
→
− ∂ ∂ ∂
×F = ∂x ∂y ∂z
= (z − 3) i + 2k
x + 2y 3z yz
Por otro lado, sabemos que la transformaci´n de coordenadas esf´ricas y
o e
rect´ngulares est´ dada por.
a a
x = a sin θ cos φ,
y = a sin θ sin φ,
z = a cos θ,
donde 0≤ θ ≤ π y 0 ≤ φ ≤ 2π. Por lo tanto, la ecuacion de la superficie S, en
2
forma param´trica est´ dada por,
e a
→(θ, φ) = a sin θ cos φi + a sin θ sin φj + a cos θ k.
−
r
de donde, el elemento diferencial de superficie est´ dado por,
a
→
−
d S = (→θ × →φ ) dθdφ = a2 sin2 θ cos φi + a2 sin2 θ sin φj + a2 sin θ cos θ k dθdφ,
−
r −
r
→
−
de esta forma, la integral de superficie de la componente normal del campo F ,
185

186. est´ dada por,
a
→ →
− −
S xF · d S = S (z − 3) i + 2k · a2 sin2 θ cos φi + a2 sin2 θ sin φj + a2 sin θ cos θ k dθdφ
2π π
= a2 (cos θ − 3) sin2 θ cos φ + 2 sin θ cos θ dθdφ
φ=0 θ=0
2π π 2π π
= a2 (cos θ − 3) sin2 θ cos φdθdφ + 2a2 sin θ cos θdθdφ,
φ=0 θ=0 φ=0 θ=0
π
como podemos observar la primera integral es igual a cero, debido a que θ=0
cos φdφ =
0, por lo tanto,
2π π 2π 2π
→ −
−
S x F · d→
s = 2a2 sin θ cos θdθdφ = 2a2 dφ sin θ cos θdθ
φ=0 θ=0 φ=0 φ=0
π
2 sin2 θ
= 2a 2π
2
θ=0
1
= 2πa2 = 2πa2 .
2
186

187. Problema 27.
Comprobar el Teorema de Green en el plano para la integral 2x − y 3 dx−
C
xydy siendo C el contorno de la regi´n en el primer cuadrante, limitada por las
o
circunferencias x2 + y 2 = 1 y x2 + y 2 = 9, como se muestra en la siguiente
figura.
Soluci´n:
o
Y
(0,3)
C4
C 1
(0,1) C 2
Y
(1,0) (3,0)
C3
Por definici´n, el teorema de Green en el plano establece que,
o
∂N ∂M
M dx + N dy = ( − )dxdy,
∂x ∂y
C Rxy
donde la trayectoria curva C encierra la regi´n que R xy que est´ en el plano
o a
XY . Como se observa en la figura, para calcular la integral de l´ ınea debemos
calcular cuatro integrales a lo largo de las trayectorias C 1 , C2 , C3 y C4 , para
esto primero necesitamos escribir en forma param´trica las ecuaciones de cada
e
trayectoria, de esta forma;
para C1 :
x = 0;
→ =
−
dr −dy j;
3 ≤ y ≤ 1,
187

188. para C2 :
x = cos θ;
y = sin θ;
π/2 ≤ θ ≤ 0;
d→ = −sinθdθ i + cos θdθ j;
−r
paraC3 :
y = 0;
d→ =
−
r dxi;
1 ≤ x ≤ 3;
para C4 :
x = 3 cos θ;
y = 3 sin θ;
0 ≤ θ ≤ π/2;
→
−
dr = −3 sin θdθ i + 3 cos θdθ j;
de esta forma, la integral de l´
ınea est´ dada por,
a
→ →
− −
f ·dr = −y 3 i − 0j · dy j
C1
+ 2 cos θ − sin3 θ i − cos θ sin θ j · − sin θdθ i + cos dθ j
C2
+ 2xi − 0j · dxi
C3
+ 6 cos θ − 27 sin3 θ i − 9 sin θ cos θ j · −3 sin θdθ i + 3 cos dθ j
C4
π/2
= −2 cos θ sin θdθ + sin4 θdθ − cos2 θ sin θdθ
θ=0
3
+ 2xdx
x=1
π/2
+ −18 cos θ sin θdθ + 81 sin4 θdθ − 27 cos2 θ sin θdθ
θ=0
π/2 π/2 π/2
x=3
= (−16 cos θ sin θdθ) + 80 sin4 θdθ − 26 cos2 θ sin θdθ + x2 x=1
,
θ=0 θ=0 θ=0
para resolver las integrales de senos y cosenos, hacemos el siguiente cambio de
variable
188

189. u = cos θ,
du = − sin θdθ,
du
dθ = − sin θ ,
por lo tanto,
π/2 π/2 π/2
→ →
− −
f ·dr = 16 udu + 26 u2 du + 40 sin2 θ (1 cos 2θ) dθ + 8
θ=0 θ=0 θ=0
2 π/2 3 π/2 π/2 π/2
16u 26u
= + +40 sin2 θdθ − 40 sin2 θ cos 2θdθ + 8
2 θ=0 3 θ=0 θ=0 θ=0
π
π/2 π/2
π 26 2
= 8 cos2 θ 2
0
+ cos3 θ + 20 (1 − cos 2θ) dθ − 20 (1 − cos 2θ) cos 2θdθ + 8
3 0 θ=0 θ=0
π/2 π/2
26 π π
= −8 − + [20θ]0 − [10 sin 2θ]0 − 20
2 2
cos 2θdθ + 20 cos2 2θdθ + 8
3 θ=0 θ=0
π/2
26 π
= −8 − + 10π − [10 sin 2θ]0 + 10
2
(1 + cos 4θ) dθ + 8
3 θ=0
π
26 π 10 2
26
= − + 10π + [10θ]0 +
2
sin4θ =− + 10π + 5π
3 4 0 3
26
= − + 15π.
3
Ahora debemos calcular la integral doble sobre la regi´n del plano XY que
o
encierra el contorno C, en este caso tenemos
M = 2x − y 3 ,
N = −xy,
por lo tanto,
∂(−xy) ∂ 2x − y 3
2x − y 3 dx−xydy =Rxy − dxdy =Rxy −y + 3y 2 dxdy
∂x ∂y
para resolver la integral anterior, es m´s conveniente usar coordenadas polares,
a
donde el elemento diferencial de area est´ dado por,
´ a
dA = dxdy = rdrdθ,
189

190. donde
y = r sin θ.
de esta forma, la integral resulta
π/2 r=3
Rxy −y + 3y 2 dxdy = −r sin θ + 3r 2 sin2 θ rdrdθ
θ=0 r=1
π/2 r=3
= −r2 sin θ + 3r 3 sin2 θ dθdr
θ=0 r=1
r=3 π/2 r=3 π/2
= − 2
r sin θdθ + 3 r3 dr sin2 θdθ
r=1 θ=0 r=1 θ=0
3 4 3 π/2
r3 π r 1
= − (− cos θ)θ=0 + 3
2
(1 − cos 2θ) dθ
3 1 4 1 2 θ=0
π
27 1 34 1 1 π 1 2
= − − +3 − (θ)θ=0 −
2
sin 2θ
3 3 4 4 2 2 θ=0
26 1 π
= − + (3) (20)
3 2 2
26
= − + 15π.
3
Por lo tanto se comprueba el teorema de Green.
190

191. Problema 28.
La esfera x2 + y 2 + z 2 = a2 intersecta a los ejes positivos X, Y y Z en los
puntos A, B y C respectivamente. La curva cerrada C consiste de tres arcos
circulares AB, BC y CA, como se muestra en la figura.
Y
C2
C3
X
C1
Z
Si el campo vectorial est´ dado por,
a
→
−
F = (y + z)i + (z + x)j + (x + z)k,
calcular
→ →
− −
F ·dr.
C
191

192. Soluci´n:
o
Como se observa en la figura, para calcular la integral de l´ ınea debemos cal-
cular tres integrales a lo largo de las trayectorias C 1 , C2 , y C3 , para esto primero
nesecitamos escribir en forma param´trica las ecuaciones de cada trayectoria,
e
de esta forma;
para la curva C1 :
x = a cos θ,
y = a sin θ,
z = 0,
0 ≤ θ ≤ 2π,
de donde, el elemento diferencial de l´
ınea est´ dada por,
a
d→1 = −a sin θdθ i + a cos θdθ j.
−
r
para la curva C2 :
y = a cos θ,
z = a sin θ,
x = 0,
0 ≤ θ ≤ 2π,
de donde, el elemento diferencial de l´
ınea est´ dada por,
a
d→2 = −a sin θdθ j + a cos θdθ k,
−
r
para la curva C3 :
z = a cos θ,
x = a sin θ,
y = 0,
0 ≤ θ ≤ 2π,
de donde, el elemento diferencial de l´
ınea est´ dada por,
a
d→3 = a cos θdθ i − a sin θdθ k,
−
r
las parametrizaciones anteriores se muestran en las figuras a), b) y c) respec-
tivamente.
192

193. Y Z Z
C1 C3
C
2
0
0 0
X Y X
a) b) c)
Por lo tanto, la integral de l´
ınea estar´ dada por:
a
→ →
− − → →
− − → →
− − → →
− −
F ·dr = F ·dr1+ F ·dr2+ F ·dr 3
C C1 C2 C3
es decir,
(0,a,0) (0,0,a) (a,0,0)
→ →
− − → →
− − → →
− − → →
− −
F ·dr = F ·dr1+ F ·dr2+ F ·dr3
C (a,0,0) (0,a,0 (0,0,a)
sustituyendo la parametrizaci´n de cada curva obtenemos,
o
θ= π
2
→ →
− −
F ·dr = (a sin θ, a cos θ, a cos θ) · (−a sin θdθ, a cos θdθ, 0)
C θ=0
θ= π
2
+ (a cos θ + a sin θ, a sin θ, a sin θ) · (0, −a sin θdθ, a cos θdθ)
θ=0
θ= π
2
+ (a cos θ, a cos θ + a sin θ, a cos θ + a sin θ) · (a cos θdθ, 0, −a sin θdθ) ,
θ=0
calculando los productos escalares y haciendo un poco de algebra obtenemos
´
θ= π
2
→ →
− −
F ·dr = a2 cos2 θ − sin2 θ + sin θ cos θ − sin2 θ + cos2 θ − sin2 θ − sin θ cos θ dθ
C θ=0
θ= π
2
= a2 2 cos2 θ − 3 sin2 θ dθ
θ=0
193

194. aplicando las identidades trigonom´tricas del seno cuadrado y coseno cuadrado,
e
obtenemos
θ= π
2
→ →
− − 1 1 1 1
F ·dr = a2 2 + cos 2θ − 3 − cos 2θ dθ
2 2 2 2
C θ=0
θ= π
2
3 3
= a2 1 + cos 2θ − + cos 2θ dθ
2 2
θ=0
θ= π
2
3 3
= a2 1 + cos 2θ − + cos 2θ dθ
2 2
θ=0
θ= π
2
1 5
= a2 − + cos 2θ dθ
2 2
θ=0
 
θ= π
2 θ= π
2
 1 5 
= a2  − dθ + cos 2θdθ  ,
2 2
θ=0 θ=0
finalmente, obtenemos
→ →
− − πa2
F ·dr =− .
4
C
194

195. Problema 29.
Dada la funci´n vectorial
o
→
−
F = axi + byj + czk,
→ →
− −
calcular S F · d S , sobre cualquier superficie que encierre una regi´n de vol-
o
umen V.
Soluci´n:
o
Para resolver este problema, aplicamos el teorema de Gauss o Teorema de
la divergencia, que establece que
→ →
− − →
−
S f · d S =V · F dV,
aplicando la definici´n de la divergencia de un campo vectorial, tenemos
o
−
→ ∂ ∂ ∂
·F = , , · (ax, by, cz)
∂x ∂y ∂z
= a + b + c,
por lo tanto, aplicando el teorema de la divergencia obtenemos,
→
− →
−
SF · dS = (a + b + c)V dV
= (a + b + c) V.
donde V es el volumen encerrado por cualquier superficie S.
195

196. Problema 30.
Calcular la siguiente integral de volumen
xyzdV,
V
donde V es el volumen limitado por los planos coordenados x = 0, y = 0, z = 0
y el plano x + 2y + z = 6.
Soluci´n:
o
Obs´rvese que en las integrales de volumen existen 6 posibles tipos de inte-
e
grales dependiendo del orden de integraci´n en el que aparezcan las variables x,
o
y e z. Por ejemplo el orden de integraci´n en el que aparece la siguiente integral,
o
   
z=z2 y=g2 (z) x=ϕ2 (y,z) 
 
 
f (x, y, z)dxdydz =  f (x, y, z)dx dy dz

 

V z=z1 y=g1 (z) x=ϕ1 (y,z)
indica que primero se debe integrar la variable x, manteniendo fijas las variables
y e z, por lo que los l´ımites de integraci´n para la variable x deben ser dos
o
funciones ϕ1 y ϕ2 de las variables y e z, este paso nos lleva finalmente a resolver
una integral doble. As´ los l´
ı ımites de integraci´n para la variable y son dos
o
funciones g1 y g2 de la variable z y finalmente los l´ımites de integraci´n para la
o
varible z son dos constantes z1 y z2 .
Para nuetro problema, podemos emplear por ejemplo el siguiente orden de
integraci´n,
o
   
x=x2 y=t2 (x) z=ψ2 (x,y) 
 
 
f (x, y, z)dxdydz =  f (x, y, z)dz  dy dx

 

V x=x1 y=t1 (x) z=ψ1 (x,y)
El volumen V se encuentra representado en la figura.
ftbpF357.8125pt299.9375pt0ptFigure
De esta forma el volumen pedido est´ dado por,
a
196

197.  6−x   
x=6 y= 2 z=6−x−2y 
 
xyzdV =  xyzdz  dy
dx

 

V x=0 y=0 z=0
 6−x 
x=6 y= 2 
 z2
6−x−2y 
= xy dz dy dx

 2 0 

x=0 y=0
 6−x 
x=6 y= 2 
  9
= x(6 − x)2 − x(6 − x)y 2 + 4xy 3 dy dx = ... = .

 
 5
x=0 y=0
Se deja como ejercicio para el lector, resolver la integral empleando cualquier
otro posible orden de integraci´n, por ejemplo puede ser el mencionado anteri-
o
ormente.
197

198. Problema 31.
Considerado el s´lido limitado por la superficie que se muestra en la siguiente
o
figura. Calcule el volumen bajo el plano z = 6 − y y sobre la regi´n x 2 + y 2 + 9.
o
Y
z = 6
− y
X
2
Z x + y2
= 9
Soluci´n:
o
En coordenadas cartecianas, para este problema podemos emplear por ejem-
plo el siguiente orden de integraci´n, que de la figura se observa que es el m´s
o a
conveniente,
   
y=y2 x=φ2 (x) z=ψ2 (x,y) 
 
 
f (x, y, z)dxdydz =  f (x, y, z)dz  dx dy.

 

V y=y1 x=φ1 (x) z=ψ1 (x,y)
198

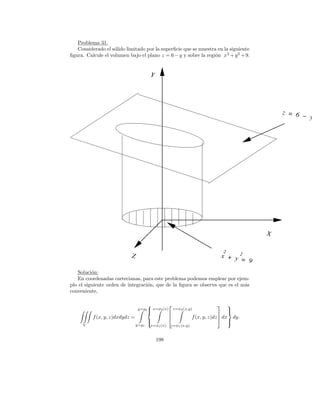
199. El volumen V se encuentra representado en la figura, en este caso f (x, y, z) =
1. De esta forma, el volumen pedido est´ dado por,
a
√
3 x= 9−y 2 z=6−y
V = √ dz dx dy
y=−3 x=− 9−y 2 z=0
√
3 x= 9−y 2
= √ (6 − y) dx dy
y=−3 x=− 9−y 2
3 √
x= 9−y 2
= 2 (6 − y) [x]x=0 dy
y=−3
3
= 2 (6 − y) 9 − y 2 dy
y=−3
3 3
= 12 9 − y 2 dy − 2 y 9 − y 2 dy.
y=−3 y=−3
La primera integral, se resuelve aplicando el siguiente cambio trigonom´trico:
e
y = 3 sin θ
dy = 3 cos θdθ
por lo que, el integrando se transforma como,
9 − y 2 −→ 9(1 − sin2 θ) −→ 3 cos θ,
π
donde los l´ımites de integraci´n son ahora desde θ = 0, hasta θ =
o 2. Por lo
tanto la primera integral est´ dada por:
a
3 3
12 9 − y 2 dy = 24 9 − y 2 dy
y=−3 y=0
θ= π
2
= 24(3)(3) cos2 θdθ
θ=0
θ= π
2
= 12(3)(3) (1 + cos 2θ) dθ
θ=0
θ= π
1 2
= 12(3)(3) θ + sin 2θ
2θ θ=0
= 54π,
199

200. obs´rvese que en la segunda integral, la funci´n a integrar es una funci´n impar,
e o o
por lo tanto esa integral es igual a cero.
Finalmente, el volumen limitado por el plano z = 6−y y la regi´n x 2 +y 2 +9,
o
como se muestra en la figura est´ dado por:
a
V = 54π.
Soluci´n Alternativa:
o
Este problema tambi´n se puede resolver en coordenadas cil´
e ındricas, por
definici´n la transformaci´n de coordenadas cil´
o o ındricas y rect´ngulares est´ dada
a a
por:
x = ρ cos φ,
y = ρ sin φ,
z = z,
de esta forma, el elemento diferencial de volumen est´ dado por,
a
dV = ρdρdφdz,
por lo tanto, el volumen pedido est´ dado por,
a
V = ρdρdφdz,
V
por comodidad, seleccionamos el siguiente orden de integraci´n,
o
φ=2π
 ρ=3 z=6−ρ sin φ 
 
V =  ρdz  dρdφ,
 
φ=0 ρ=0 z=0
por lo tanto,
200

201. φ=2π
 ρ=3 
 
z=6−ρ sin φ
V = ρ [z]z=0 dρdφ
 
φ=0 ρ=0
φ=2π
 ρ=3 
 
= ρ (6 − ρ sin φ) dρ dφ
 
φ=0 ρ=0
φ=2π
 ρ=3 
 ρ3 ρ=3 
= 3ρ2 − sin φ dφ
 3 ρ=0 
φ=0 ρ=0
φ=2π
27
= 27 − sin φ dφ,
3
φ=0
finalmente obtenemos,
φ=2π
27
V = 27φ + cos φ
3 φ=0
27 27
= 27(2π) + cos(2π) − 0 + cos(0)
3 3
27 27
= 54π + −
3 3
= 54π.
Como se puede observar, en coordenadas cil´
ındricas es m´s simple la soluci´n.
a o
201

202. Problema 32:
→
−
Dado el campo vectorial F = 2xyi + 3yzj + 4xzk calcular,
→
−
V × F dV,
siendo V, el volumen limitado por los planos x = 0, y = 0, z = 0 y 2x+2y+z =
4.
Soluci´n:
o
Para nuetro problema, podemos emplear por ejemplo el siguiente orden de
integraci´n,
o
   
x=x2 y=t2 (x) z=ψ2 (x,y) 
→
−  →
− 
 
× F dxdydz =  × F dz  dy dx

 

V x=x1 y=t1 (x) z=ψ1 (x,y)
El volumen V de integraci´n se encuentra representado en la figura.
o
ftbpF291.9375pt280.6875pt0ptFigure
→
−
Calculemos primero el rotacional del campo vectorial F de la forma,
i j k
→
− ∂ ∂ ∂
×F = ∂x ∂y ∂y
= −3y i − (4z − 0) j + zxk
2zy 3yz 4xz
→
−
×F = −3y i − 4z j − 2xk.
De la figura, nuestros l´
ımites de integraci´n est´n dados por:
o a
0 ≤ z ≤ 4 − 2x − 2y
0≤y ≤2−x
0≤x≤2
de esta manera podemos escribir nuestra integral de volumen de la forma,
2 2−x
→
− 4−2x−2y
V × F dV = − z=0 (3y, 4z, 2x) dzdydx
x=0 y=0
2 2−x
4−2x−2y 4−2x−2y 4−2x−2y
= − [3yz]z=0 , 2z 2 z=0
, [2xz]z=0 dy dx
x=0 y=0
2 2−x
2
= − 12y − 6xy − 6y 2 , 2 (4 − 2x − 2y) , 8x − 4x2 − 4xy dy dx,
x=0 y=0
202

203. obs´rvese que las integrales con respecto a la variable y son inmediatas, a´n as´
e u ı,
para la integral de la componente en y hacemos el siguiente cambio de variable,
u = 4 − 2x − 2y,
du = −2dy
por lo tanto,
 
3 2−x
2
→
−  6y 2 − 3xy 2 − 2y 3 2−x , − (4 − 2x − 2y) 2−x
 dx,
V × F dV = − y=0
, 8xy − 4x2 − 4xy 2 y=0
x=0 3
y=0
al evaluar los l´
ımites de integraci´n de la variable y, despues de algunos pasos
o
algebraicos obtenemos,
2
−
→ 3 1 3
V × F dV = − (2 − x) , (4 − 2x) , 2x3 − 8x2 + 8x dx
x=0 3
de donde, al integral la variable x, obtenemos
4 2
→
− (2 − x) 1 4 x4 8
V × F dV = − − , − (4 − 2x) , − x3 + 4x2
4 24 2 3
x=0
24 1 64
= − 0− ,− 0 − 44 , 8 − + 16
4 24 3
32 8
= − 4, , ,
3 3
203

204. finalmente, obtenemos
→
− 32 8
V × F dV = −4i − j − k.
3 3
El problema tambi´n se puede resolver, considerando el siguiente orden de
e
integraci´n,
o
4 2− z 1
2−y− 2 z
→
− 2
V × F dV = (−3y, −4z, −2x) dxdydz
z=0 y=0 x=0
donde nuestra regi´n de integraci´n se encuentra ahora en el plano Y Z, es decir,
o o
1
0 ≤ x ≤ z − y − 2 z,
z
0 ≤ y ≤ 2 − 2,
0 ≤ z ≤ 4,
efectuando la integraci´n primero con respecto a la variable x obtenemos,
o
4 2− z
→
− 2 z z z 2
V × F dV = −3y 2 − y − , −4z 2 − y − ,− 2 − y − dy dz
z=0 y=0 2 2 2
4 2− z
3 1 z 3 2
= −3y + y + y 2 z , −8yz + 2y 2 z + 2yz 2 ,
2 3
2−y− dz
z=0 4 3 2 y=0
...
4
z3 3 z3 1 z 3
= − z 2 + 3z − 4 , − + 4z 2 − 8z , − 2− dz
z=0 16 4 2 3 2
4
z4 1 3 z4 4 1 z 4
= − z 3 + z 2 − 4z , − + z 3 − 4z 2 , 2− ,
64 4 2 8 3 6 2 z=0
finalmente al evaluar los l´
ımites de la variable z, obtenemos
→
− 32 8
V × F dV = −4i − j − k.
3 3
Donde los pasos intermedios que faltan, el lector los puede completar y son
an´logos a los del primer orden de integraci´n.
a o
204

205. Problema 33.
→
−
Dado el campo vectorial F (x, y, z) = 2yz i−(x+3y−2)j +(x2 +z)k, Calcular
→ →
− −
la integral de superficie × F · d S extendida a la superficie de intersecci´n
o
S
ındros x2 + y 2 = a2 y x2 + z 2 = a2 situada en el primer octante.
de los cil´
Soluci´n:
o
En este problema, aplicaremos el teorema del rotacional de Stokes que
establece,
→ −
− → → →
− −
× F · dS = F ·dr,
S C
es decir, la integral de superficie de la componente normal del rotacional de un
campo vectorial, tomada sobre una superficie cerrada, es igual a la integral de
l´
ınea de la componente tangencial del campo vectorial, tomada sobre la curva
cerrada que limita o rodea a la superficie.
La siguiente figura muestra la intersecci´n de los cil´
o ındros. Aplicando el
teorema del rotacional de Stokes, la integral de superficie ser´ igual a la integral
a
de l´
ınea formada por las trayectorias C1 , C2 , C3 y C4 como se ilustra en la
figura, es decir una curva simple que encierra la intersecci´n de los cil´
o ındros
est´ formada por dos trayectorias rectas C2 y C3 y dos arcos circulares C1 y C4 .
a
Z
C3
(0,α,0)
C4 (0,α,α)
C2
( a ,U,U)
X
( α,U,U)
C1
Y
Aplicando el teorema del rotacional de Stokes obtenemos,
205

206. → →
− − → →
− −
× F · dS = F ·dr
S C
→ →
− − → →
− − → →
− − → →
− −
= F ·dr + F ·dr + F ·dr + F ·dr.
C1 C2 C3 C4
Para la primera trayectoria recta C2 (ver figura) las ecuaciones param´tricas
e
est´n dadas por:
a
x = 0
y = a
0 ≤ z ≤ a,
de donde → = aj + z k, as´ el elemento diferencial de l´
−
r ı ınea est´ dado por:
a
d→ = dz k,
−
r
por lo tanto la integral de l´
ınea para la trayectoria C 2 est´ dada por:
a
→ →
− −
F ·dr = 2az i − (3a − 2)j + z k · dz k
C1 C1
a a
z2 a2
= zdz = = .
2 0 2
z=0
Para la segunda trayectoriarecta recta C3 (ver figura) las ecuaciones param´tricas
e
est´n dadas por:
a
x = 0
z = a
0 ≤ y ≤ a,
de donde → = y j + ak, as´ el elemento diferencial de l´
−
r ı ınea est´ dado por:
a
206

207. d→ = dy j,
−
r
por lo tanto la integral de l´
ınea para la trayectoria C 3 est´ dada por:
a
→ →
− −
F ·dr = 2yai − (3y − 2)j + ak · dy j
C3 C3
 a a

a
3y 2
= − 2dy − 3ydy  = −2y + ,
2 0
y=0 y=0
finalmente obtenemos,
→ → 3a2
− −
F ·dr = − 2a.
2
C3
Para la primera trayectoria circular C1 (ver figura) las ecuaciones param´tricas
e
est´n dadas por:
a
x = a cos φ,
z = a sin φ,
y = 0,
en donde el par´metro φ ∈ [0, π ], en este caso se tiene → = a cos φi + a sin φk,
a 2
−
r
as´ el elemento diferencial de l´
ı ınea est´ dado por:
a
d→ = −a sin φdφi + a cos φdφk,
−
r
por lo tanto la integral de l´
ınea para la trayectoria circular C 1 est´ dada por:
a
→ →
− −
F ·dr = −(3a sin φ − 2)j + ((a cos φ)2 + a sin φ)k · −a sin φdφi + a cos φdφk
C1 C3
π π π
2 2 2
= − a3 cos3 φ + a2 sin φ cos φ dφ = −a3 cos3 φdφ − a2 sin φ cos φdφ,
φ=0 φ=0 φ=0
207

208. la primera integral se evalua aplicando la identidad trigonom´trica
e
1 1
cos3 = cos2 φ cos φ = + cos 2φ cos φ,
2 2
la segunda integral es inmediata de la forma udu, finalmente al integrar y evaluar
las integrales obtenemos,
π π
→ →
− − 3 sin3 φ 2
2 cos2 φ 2
F ·dr = a − sin φ +a
3 0 2 0
C3
2 a2
= − a3 − .
3 2
Finalmente para la trayectoria circular C4 (ver figura) las ecuaciones param´tricas
e
est´n dadas por:
a
x = a cos φ
y = a sin φ
z = 0,
en donde el par´metro φ ∈ [0, π ], en este caso se tiene → = a cos φi + a sin φj,
a 2
−
r
as´ el elemento diferencial de l´
ı ınea est´ dado por:
a
d→ = −a sin φdφi + a cos φdφj,
−
r
por lo tanto la integral de l´
ınea para la trayectoria circular C 4 est´ dada por:
a
→ →
− −
F ·dr = −(a cos φ + 3a sin φ − 2)j + ((a cos φ)2 + a sin φ)k ·
C4 C3
−a sin φdφi + a cos φdφj ,
es decir,
208

209. π
2
→ →
− −
F ·dr = −a2 cos2 φdφ − 3a2 sin φ cos φdφ + 2a cos φdφ
C4 φ=0
π π π
2 2 2
= −a2 cos2 φdφ − 3a2 sin φ cos φdφ + 2a cos φdφ,
φ=0 φ=0 φ=0
la primera integral se evalua aplicando la identidad trigonom´trica,
e
1 1
cos2 φ = + cos 2φ ,
2 2
la segunda y tercera integrales son inmediatas, por lo tanto
π π
→ →
− − φ sin 2φ 2
cos2 φ 2 π
F · d r = −a2 − + 3a 2
+ [2a sin φ]0 ,
2
2 4 0 2 0
C4
finalmente al evaluar las integrales obtenemos,
→ →
− − πa2 3
F ·dr =− − a2 + 2a.
4 2
C4
Por lo tanto, la integral de l´
ınea a lo largo de la trayectoria curva simple que
encierra la intersecci´n de los cil´
o ındros como se muestra en la figura, se obtiene
al sumar los resultados de las trayectorias C1 , C2 , C3 y C4 es decir;
→ →
− − → →
− − → →
− − → →
− − → →
− −
F ·dr = F ·dr + F ·dr + F ·dr + F ·dr
C C1 C2 C3 C4
2 2 2
a 3a 2 a πa2 3
= + − 2a + − a3 − + − − a2 + 2a
2 2 3 2 4 2
2
2 πa
= − a3 − .
3 4
209

210. Finalmente, aplicando el teorema del rotacional de Stokes se obtiene
→ →
− − → →
− − 2 πa2
× F · dS = F · d r = − a3 − .
3 4
S C
210

211. Problema 34.
Verificar el teorema de la divergencia de Gauss para
→
−
F (x, y, z) = (2x − y)i − (2y − z)j + z k,
donde V es el volumen encerrado por la superficie S formada por los planos
coordenados x = 0, y = 0, z = 0 y el plano x + 2y + z = 6.
Soluci´n:
o
El volumen V que encierra la superficie S se muestra en la siguiente figura.
Z
B(0,0,6)
2y + z = 6
x + y =6
S3
S1
O
Y
C(0,3,0)
S2
x + 2y = 6
A(6,0,0)
X
Como se muestra en la figura, la superficie S est´ formada por 4 superficies
a
S1 (ABO), S2 (ACO), S3 (BCO) y S4 (ABC), por lo tanto para calcular la inte-
211

212. →
−
gral de superficie debemos de calcular el flujo de F a trav´s de cada superficie,
e
es decir;
→ →
− − →
− →
− →
− →
−
F · dS = F · ndS + F · ndS + F · ndS + F · ndS
S S1 S2 S3 S4
De la figura se observa lo siguiente:
Para la superficie S1 (ABO);
y = 0, n = −j y dS = dxdz.
Para la superficie S2 (ACO);
z = 0, n = −k y dS = dxdy
Para la superficie S3 (ABO);
x = 0, n = −i y dS = dydz.
por lo tanto, las integrales para estas superficies resultan,
→
−
F · ndS = (2x − y)i − 2y j · −k dxdy = 0
S1 S1
→
−
F · ndS = 2xi + z j + z k · −j dxdz
S2 S2
6 x=6−z 6
= − zdxdz = − z(6 − z)dz
z=0 x=0 z=0
6
z3
= −3z 2 + = −36.
3 z=0
→
−
F · ndS = −y i − (2y − z)j + z k · −i dydz
S3 S3
6−z
6 y= 2 6
(6 − z)2
= − ydydz = dz
8
z=0 y=0 z=0
3 6
(6 − z)
= − = 9.
24 z=0
212

213. Para resolver la integral sobre la superficie S4 (ABC), aplicamos el teorema
de la proyecci´n de la superficie sobre un plano coordenado, que establece
o
→
−
− →
→ − f ·n
F ·d S = dxdy.
S4 Rxy
n·k
Para la superficie S4 (ABC) aplicando la definici´n del gradiente, un vector
o
→
−
normal a la superficie est´ dado por N = i + 2j + k, as´ en este caso el vector
a ı
b b b
n est´ dado por n = i+2j+k de donde se sigue que:
a √
6
→
− i + 2j + k
F ·n = (2x − y)i − (2y − z)j + z k · √
6
1
= √ (2x − 5y + 3z) ,
6
empleando la ecuaci´n para la superficie S4 (ABC) se tiene z = 6−x−2y,sustituyendo
o
en la expresi´n anterior obtenemos
o
→
− 1
F · n = √ (18 − x − 11y),
6
tambi´n obtenemos,
e
i + 2j + k 1
n·k = √ ·k = √ .
6 6
De los resultados anteriores, la integral para la superficie S 4 (ABC) est´ dada
a
por:
1 6 x=6−2y
− →
→ − √ (18
6
− x − 11y)
F ·d S = Rxy 1 dxdy = [18 − x − 11y] dxdy
√
S4 6 y=0 x=0
6 6−2y 6
x2
= 18 − − 11xy dy = 90(1 − y) + 20y 2 dy,
2 x=0
y=0 y=0
finalmente al calcular la integral en y, evaluando los l´
ımites de integraci´n obten-
o
emos,
3
− →
→ − 20y 3
F ·d S = 90y − 45y 2 − = 45,
3 y=0
S4
213

214. sumando los resultados obtenidos para las superficies S 1 (ABO), S2 (ACO),
S3 (BCO) y S4 (ABC), obtenemos
→ →
− −
F · d S = (−36) + 0 + 9 + 45 = 18.
S
Para resolver la integral de volumen, si aplicamos la definici´n de la diver-
o
→
− →
−
gencia de un campo vectorial F en este problema tenemos que · F = 1;
por otro lado, observemos en la figura la regi´n de volumen que encierran las
o
superficies S1 (ABO), S2 (ACO), S3 (BCO) y S4 (ABC), por lo tanto
6−z
6 2 6−2y−z
→
−
· F dV = dxdyxz
V z=0 y=0 x=0
 6−z

6 
 2 
 6
6−z
= [6 − 2y − z] dy dz = y (6 − z) − y 2 2
y=0
dy

 

z=0 y=0 z=0
6 6
(6 − z)2 (6 − z)2 1
= (6 − z) − dz = (6 − z)2 dz
2 4 4
z=0 z=0
3 6
(6 − z)
= − = 18,
12 z=0
que es el mismo resultado que se obtuvo al calcular la integral de superficie. Por
lo tanto, se ha verificado el teorema de la divergencia de Gauss.
214

215. Problema 35.
→ −
−
Sea F = →, verificar el teorema de la divergencia de Gauss donde S es la
r
superficie que consta del cono z 2 = x2 + y 2 para 0 ≤ x2 + y 2 ≤ 1 y la superficie
que es el disco x2 + y 2 ≤ 1, z = 1 como se muestra en la siguente figura:
Z
S2 : 2 2
x + y = 1
S1 : 2 2
z = x + y
Y
X
Soluci´n:
o
Debemos verificar que,
→
− →
− →
−
SF · d S =V · F dV,
primeramente calculemos la integral de superficie, como se ilustra en la figura
anterior, la superficie S est´ formada por las superficies S 1 y S2 , de esta forma
a
215

216. → · d→ = → · d→ + → · d→
− −
r S S1 −
r
−
S S2 −
r
−
S
S
Para S1 :
Aplicando la definici´n del gradiente, donde φ (x.y.z) = x 2 + y 2 − z 2 = 0
o
obtenemos,
φ
n =
| φ|
2xi + 2y j − 2z k
=
4x2 + 4y 2 + 4z 2
xi + y j − z k
= ,
x2 + y 2 + z 2
xb b b
observe que el vector n = √ i+yj−zk 2 , es normal interior (hacia adentro de S1 ),
2 2 x +y +z
por lo tanto
→ · d→
− −
r S = → · ndS
−
r
S1 S1
xi + y j − z k
= S1 xi + y j + z k · dS
x2 + y 2 + z 2
x2 + y 2 − z 2
= S2 dS
x2 + y 2 + z 2
= 0.
Para S2 :
De la figura, obs´rvese que el vector unitario normal a S 2 es n = k, de
e
donde obtenemos inmediatamente que
n · → = z,
−
r
adem´s como z = 1, entonces la integral sobre la superficie S 2 est´ dada por:
a a
→ · ndS = dS ,
−
r
S2 2 S2 2
216

217. 2
pero S2 dS2 = π (1) , es decir, el area de un c´
´ ırculo de radio 1, por lo tanto
→ · d→ = π.
− −
r S
S2
Por lo tanto la integral sobre la superficie S del problema est´ dada por:
a
(1) → · d→ = → · d→ + → · d→ = π.
− −
r S S1 −
r
−
S S2 −
r
−
S
S
Por otro lado,
V ·→
−
r = 3V dV
1 2
= 3 π (1) (1)
3
que es igual al volumen de un cono de altura uno y radio 1, finalmente obtenemos
(2) V ·→=π
−
r
Por lo tanto, de los resultados (1) y (2) se verifica el Teorema de la diver-
gencia de Gauus, es decir,
→ · d→ =
− −
r S V
→
−
· F dv = π.
S
217