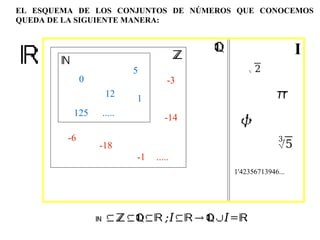
El documento describe las propiedades fundamentales de los números racionales. Explica que los números racionales forman un conjunto con reglas algebraicas como la clausura, los elementos identidad y los elementos inversos para la suma y la multiplicación, así como las propiedades asociativas, conmutativas y distributivas. Luego identifica cuáles propiedades ilustran cada uno de los siete enunciados dados como ejemplos.

1. EL ESQUEMA DE LOS CONJUNTOS DE NÚMEROS QUE CONOCEMOS
QUEDA DE LA SIGUIENTE MANERA:
5
0
12 1
125 .....
-3
-14
-6
-18
-1 .....
I
2
1'42356713946...
3
5
;I I

2. Propiedades de los
Números Racionales
●
Son postulados que no requieren
demostración
●
Forman un conjunto de reglas
fundamentales para fácil manejo
algebraico
●
Si p, q, r son tres números
racionales cualesquiera y
pertenecen al conjunto de los
números reales veamos las
propiedades:

3. Clausura
De la suma
p + q
La suma de dos
números reales
es otro número
real
De la
multiplicación
p q
El producto de
dos números
reales es otro
número real

4. Elemento Identidad o Neutro
De la suma
p + 0 = p
0 + p =
p
El número 0 es el
único elemento
que conserva la
identidad en la
operación de
De la multiplicación
p ⋅ 1 = p
1 ⋅ p = p
El número 1 es
el único
elemento que
conserva la
identidad en la
operación de
multiplicación

5. Elemento Inverso
De la suma
p + –
p =
0
Para todo
número p existe
un número –
p
llamado inverso
aditivo (opuesto)
que genera su
De la multiplicación
p ⋅ = 1
Para todo número
p (excepto 0)
existe un
número
llamado inverso
multiplicativo
(recíproco) que
genera su
p
1
p
1

6. Asociativa
De la suma
(p + q) + r = p +
(q + r)
De la
multiplicación
(p q) r = p (q r)
En ambos casos la forma en que se
agrupan no alteran el resultado final ni en
la suma ni en la multiplicación.
Esto no aplica en la resta ni en la
división.

7. Conmutativa
De la suma
p + q = q
+ p
De la
multiplicación
p q = q p
En la suma y en la multiplicación el orden
no altera el resultado.
Esto no aplica en la resta ni en la
división.

8. Distributiva
De la suma
p(q + r) = pq + pr
(q + r)p = qp + rp
Aquí la multiplicación distribuye a la
suma y puede extenderse a varios
números dentro del paréntesis

9. Identifica la propiedad en
cada enunciado:
7 + 5 = 5 + 7
3 + (5 + 2) = 3 + (2 + 5)
(6 ⋅ 3) 1 = 6 (3 ⋅ 1)
5(3 + 2) = 5(3) + 5(2)
7 ⋅ 1 = 7
11 + 0 = 11
9 + -9 = 0
1)
2)
3)
4)
5)
6)
7)

10. Identifica la propiedad en
cada enunciado:
7 + 5 = 5 + 7
3 + (5 + 2) = 3 + (2 + 5)
(6 ⋅ 3) 1 = 6 (3 ⋅ 1)
5(3 + 2) = 5(3) + 5(2)
7 ⋅ 1 = 7
11 + 0 = 11
9 + -9 = 0
1)
2)
3)
4)
5)
6)
7)