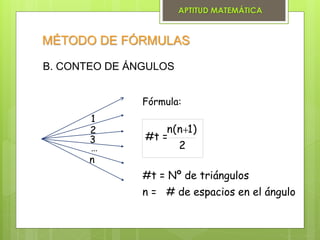
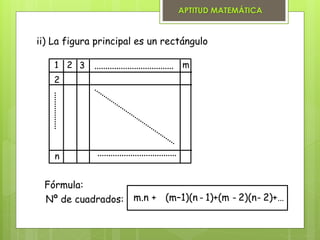
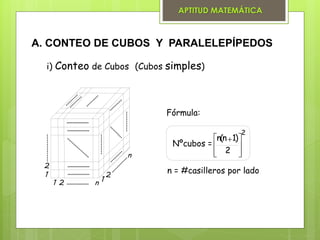
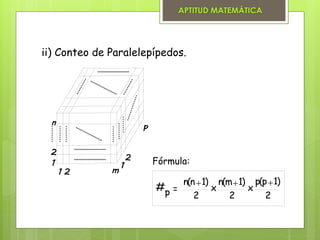
El documento presenta varios métodos para contar figuras geométricas. Describe el método combinatorio que asigna números a las partes de una figura y cuenta las combinaciones. También presenta el método de fórmulas, el cual proporciona fórmulas matemáticas para contar segmentos, triángulos, cuadriláteros, cuadrados y cubos/paralelepípedos dependiendo de la cantidad de espacios en la figura. Finalmente, muestra ejemplos de cómo aplicar estos métodos para resolver problemas de conteo.

1. CONTEO DE
FIGURAS
Prof. Widman Gutiérrez R.
APTITUD MATEMÁTICA

2. MÉTODOS DE CONTEO
MÉTODO COMBINATORIO
El presente método consiste en anotar un número
o símbolo en c/u de las partes de la figura, de
modo que cada nueva figura que detectemos
quede asociada a un número o combinación de
números. Luego contamos las combinaciones
anotadas y el resultado será la cantidad pedida.
APTITUD MATEMÁTICA

3. EJEMPLO 1
¿Cuántos triángulos hay en esta figura?
APTITUD MATEMÁTICA

4. Solución
Los triángulos son:
De (1) : 1; 2; 3; 4; 5; 6; 7; 8 = 8
De (2) 12; 34; 56; 78 = 4
De (4) : 1234; 5678; 7812; 3456 = 4
Rpta: 16 triángulos
Colocamos un dígito a cada parte:
1 2
3
4
56
7
8
APTITUD MATEMÁTICA

5. MÉTODO DE FÓRMULAS
Fórmula:
#s = Nº de segmentos
n = # de espacios sobre la línea.
#s =
2
)1n(n +
A. CONTEO DE SEGMENTOS
1 2 3 … n-1 n
APTITUD MATEMÁTICA

6. #t =
2
)1n(n +
#t = Nº de triángulos
n = # de espacios en el ángulo
MÉTODO DE FÓRMULAS
1
2
3
…
n
B. CONTEO DE ÁNGULOS
Fórmula:
APTITUD MATEMÁTICA

7. #t =
2
)1n(n +
#t = Nº de triángulos
n = # de espacios en la base
MÉTODO DE FÓRMULAS
1 2 3 … n
C. CONTEO DE TRIÁNGULOS
Fórmula:
APTITUD MATEMÁTICA

8. MÉTODO DE FÓRMULAS
D. CONTEO DE CUADRILÁTEROS
i) Primera forma
1 2 3 … 4
Fórmula:
2
)1n(n
c1#
+
=
#c = Nº de cuadriláteros
n = # espacios en la base
APTITUD MATEMÁTICA

9. APTITUD MATEMÁTICA
m
:
2
1 2 3 4 … n
Fórmula:
4
)1m(m)1n(n
c#
++
=
n = #casilleros en la base
m = # casilleros sobre un lado
ii) Segunda forma

10. APTITUD MATEMÁTICA
A. CONTEO DE CUADRADOS:
i) La figura principal es un cuadrado
Fórmula
:
La figura debe ser un cuadrado de n
n = # de casilleros por lado.
1
2
3
4
n
2 3 4 n
# =
6
)1n2)(1n(n ++
S

11. APTITUD MATEMÁTICA
ii) La figura principal es un rectángulo
Fórmula:
Nº de cuadrados:
2
n
1 2 3 m
m.n + (m–1)(n - 1)+(m - 2)(n- 2)+…

12. APTITUD MATEMÁTICA
A. CONTEO DE CUBOS Y PARALELEPÍPEDOS
i) Conteo de Cubos (Cubos simples)
1
2
1 2 n 1
2
n
Fórmula:
Nºcubos =
2
2
)1n(n







 +
n = #casilleros por lado

13. APTITUD MATEMÁTICA
ii) Conteo de Paralelepípedos.
Fórmula:1
1 2
2
n
m
1
2
p
p 2
)1p(p
x
2
)1m(n
x
2
)1n(n +++
# =