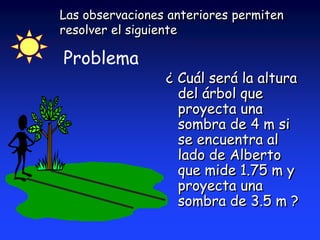
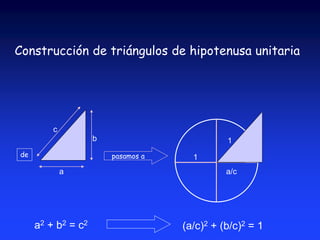
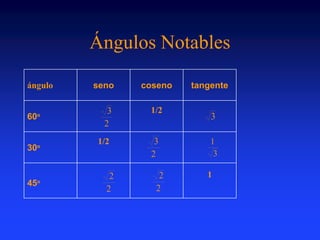
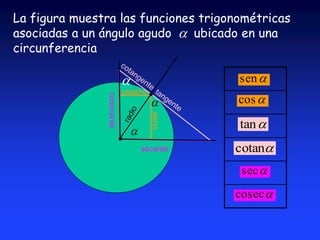
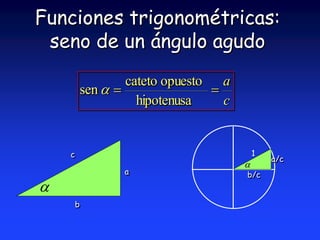
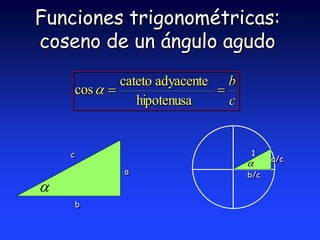
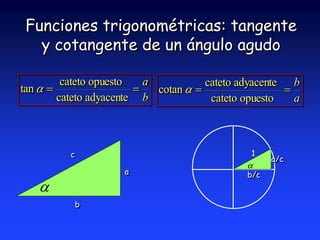
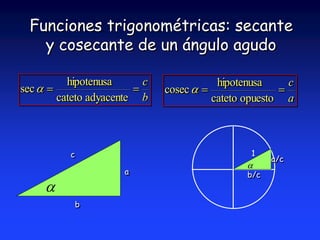
Este documento introduce la trigonometría y las funciones trigonométricas. Brevemente explica que la trigonometría estudia la relación entre los ángulos y lados de un triángulo y permite determinar lados y ángulos desconocidos. Luego define las seis funciones trigonométricas principales (seno, coseno, tangente, cotangente, secante y cosecante) y cómo se calculan en triángulos rectángulos y triángulos normalizados de hipotenusa unitaria.

1. Introducción a la trigonometría
y a las funciones trigonométricas

2. Un poquito de historia
Trigonometría es una palabra de etimología
griega, aunque no es una palabra griega. Se
compone de trigonon que significa triángulo
y metria que significa medición. Y se habla
de ella como matemática práctica.

3. La trigonometría resuelve el siguiente
problema: conocidos algunas de las
componentes de un triángulo, determinar las
restantes
La geometría (teórica) nos dice cuándo ciertos
datos determinan que salvo por posición un
triángulo de lados dados, la trigonometría
(práctica) nos dice cómo calcular los restantes.

4. Ángulos
• ÁNGULOS Y CUADRANTES
• Todas circunferencia al ser cortada por los ejes de coordenadas , queda
dividida en cuatro partes iguales independientemente de la medida del radio.
Cada una de dichas partes se llama CUADRANTE y se numeran en sentido
antihorario, al igual que los ángulos.
• El 1º Cuadrante iría de 0º a 90º (de 0 a Π/2 radianes)
• El 2º Cuadrante iría de 90º a 180º (de Π /2 a n radianes)
• El 3º Cuadrante iría de 180º a 270º (de Π a 3 Π /2 radianes)
• y El 4º Cuadrante iría de 270º a 360º (de Π n/2 a 2 Π radianes)
• A todos los efectos, si un ángulo o suma de ángulos pasara de 360º, se le resta
tantas veces 360º como sea necesario.
• Así, tener 370º es como tener 10º, tener 750º es como tener 30º.

5. El radian
• EL RADIAN
• Un radian será aquel ángulo cuyo ARCO mide IGUAL que el RADIO que lo
forma. Esa medida es independiente del valor del radio. Una circunferencia tiene 2.n
radianes.
• Un radian valdrá : 360º
• Π rad = ------ = 180º
• 2. Π
• SUMA DE ÁNGULOS
• En todo triángulo la suma de sus tres ángulos es siempre de 180º. El inconveniente
de esta propiedad es que para conocer un ángulo es necesario saber la medida de los
otros dos. Ese inconveniente se salva con la Trigonometría.
• TRIGONOMETRÍA.- Es la parte de las matemáticas que estudia la relación
entre los ángulos y los lados de un triángulo.

6. Trigonometría
Comencemos con triángulos rectángulos.
a
c
b
Si conocemos dos de los lados
del triángulo, como el Teorema
de Pitágoras afirma que
a2 + b2 = c2,
conocemos el tercer lado.
Eso sí, debemos saber si los
lados que conocemos son catetos
o la hipotenusa.

7. Resolución de triángulos rectángulos.
Pero no tenemos ninguna información acerca de los
ángulos. A continuación comenzaremos a abordar este
problema.
Dividimos los catetos en r partes iguales, y
formamos una retícula. Los catetos de los
triángulos de las esquinas miden a/r, b/r y
su hipotenusa será, por el Teorema de
Pitágoras igual a c/r.
NOTEMOS que la hipotenusa pasa por los
puntos de la retícula. Los triángulo de las
esquinas tienen los mismos ángulos.

8. Las observaciones anteriores permiten
resolver el siguiente
¿ Cuál será la altura
del árbol que
proyecta una
sombra de 4 m si
se encuentra al
lado de Alberto
que mide 1.75 m y
proyecta una
sombra de 3.5 m ?
Problema

9. Sigamos con el problema de encontrar los
ángulos en triángulos rectángulos.
Vamos a escoger triángulos “normalizados”, que
representen a cada triángulo rectángulo.
Tomaremos triángulos con hipotenusa unitaria.

10. Construcción de triángulos de hipotenusa unitaria
c
a
a2 + b2 = c2
b
a/c
b/c
(a/c)2 + (b/c)2 = 1
pasamos a
1
de 1

11. Ángulos Notables
ángulo seno coseno tangente
60o
1/2
30o
3
1/2
45o
1
1
2
3
2
3
3
2
2
2
2

12. Ángulos Notables
ángulo
0° y
360°
90° 180° 270°
sen
0 1 0 -1
cos 1 0 -1 0
tan
0 ∞ 0 -∞

13. La figura muestra las funciones trigonométricas
asociadas a un ángulo agudo ubicado en una
circunferencia
 sen
 cos
 tan
cotan
sec 
cosec 

secante
cosecante
seno
coseno




14. Funciones Trigonométricas

P
l
 en
cuadr.
I II III IV
sen 
csc 
+ + - -
cos 
sec 
+ - - +
tan 
cot 
+ - + -
P
 P
 P
Todos
Sen
Csc
Tan
Cot
Cos
Sec

15. Funciones trigonométricas:
seno de un ángulo agudo

a
c
cateto opuesto
 
hipotenusa
sen 
a
b
c

b/c
a/c
1

16. Funciones trigonométricas:
coseno de un ángulo agudo

b
c
cateto adyacente
 
hipotenusa
cos 
a
b
c

b/c
a/c
1

17. Funciones trigonométricas: tangente
y cotangente de un ángulo agudo

a
cateto opuesto
b
c
cateto adyacente

b/c
a/c
1
a
b
 
cateto adyacente
tan 
b
a
 
cateto opuesto
cotan 

18. Funciones trigonométricas: secante
y cosecante de un ángulo agudo

a
hipotenusa
b
c
hipotenusa

b/c
a/c
1
c
b
 
cateto adyacente
sec 
c
a
 
cateto opuesto
cosec 