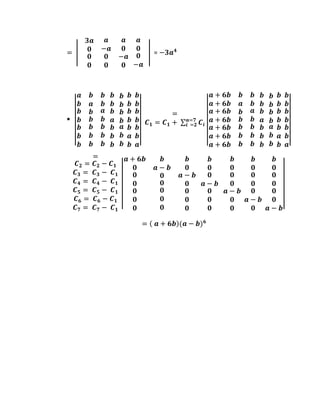
1. El documento describe propiedades de los determinantes, incluyendo que el valor absoluto de un determinante no cambia al intercambiar filas o columnas, y que el determinante de una matriz producto es igual al producto de los determinantes. 2. También explica operaciones elementales que no cambian el valor de un determinante, como multiplicar una fila por un escalar o sumar múltiplos de filas. 3. Finalmente, presenta ejemplos de determinantes de Vandermonde y el método del acumulador.

1. PROPIEDADES DE LOS DETERMINANTES
1. |A t |= |A|
2. |A|=0 Si:
Posee dos líneas iguales
Todos los elementos de una línea son nulos.
Los elementos de una línea son combinación lineal de las
otras.
3. Un determinante triangular es igual al producto de los
elementos de la diagonal principal.
4. Si en un determinante se cambian entre sí dos líneas
paralelas su determinante cambia de signo.
5. Si a los elementos de una línea se le suman los elementos de
otra paralela multiplicados pr eviamente por un nº real el
valor del determinante no varía.
6. Si se multiplica un determinante por un número real, queda
multiplicado por dicho número cualquier línea, pero sólo
una.
7. Si todos los elementos de una fila o columna están formados
por dos sumandos, dicho determinante se descompone en la
suma de dos determinantes.

2. 8. |A·B| =|A|·|B|
OPERACIONES ELEMENTALES DE FILA O COLUMNA
EN UN DETERMINANTE
1. Multiplicar una fila o una columna por un escalar no nulo el determinante
queda multiplicado por dicho escalar.
Notación:
2. Intercambiar de posición dos filas o columnas el determinante queda
multiplicado por -1.
Notación:
3. Sumar a una fila o columna y un múltiplo de otra el valor del determinante no
cambia.
Notación:
Ejercicio:
Para que valores de λ el determinante es diferente de cero.
1. Usando el método de Sarrus

3. 2. Usando la propiedad tres de los determinantes
Ejemplo 1:
=
Ejemplo 2:
DETERMINANTE DE VANDERMONDE
Un determinante de Vandermonde es un determinante que presenta
una progresión geométrica en cada fila o en cada columna, siendo el
primer elemento 1.

4. Ejemplo 1:
Ejemplo 2:
1 1 1 1 1 1
b a c a 1 1
a b c 0 b-a c-a (b a )( c a)
b(b a ) c(c a ) b c
a2 b2 c2 0 b 2 - ab c 2 ac
(b a)(c a)(c b)
MÉTODO DEL ACUMULADOR
Este método consiste en sumar todos los elementos de todas las filas y
columnas en una sola, si y solo si los elementos de las demás filas o columnas
suman lo mismo.
Ejemplos:


5. =
