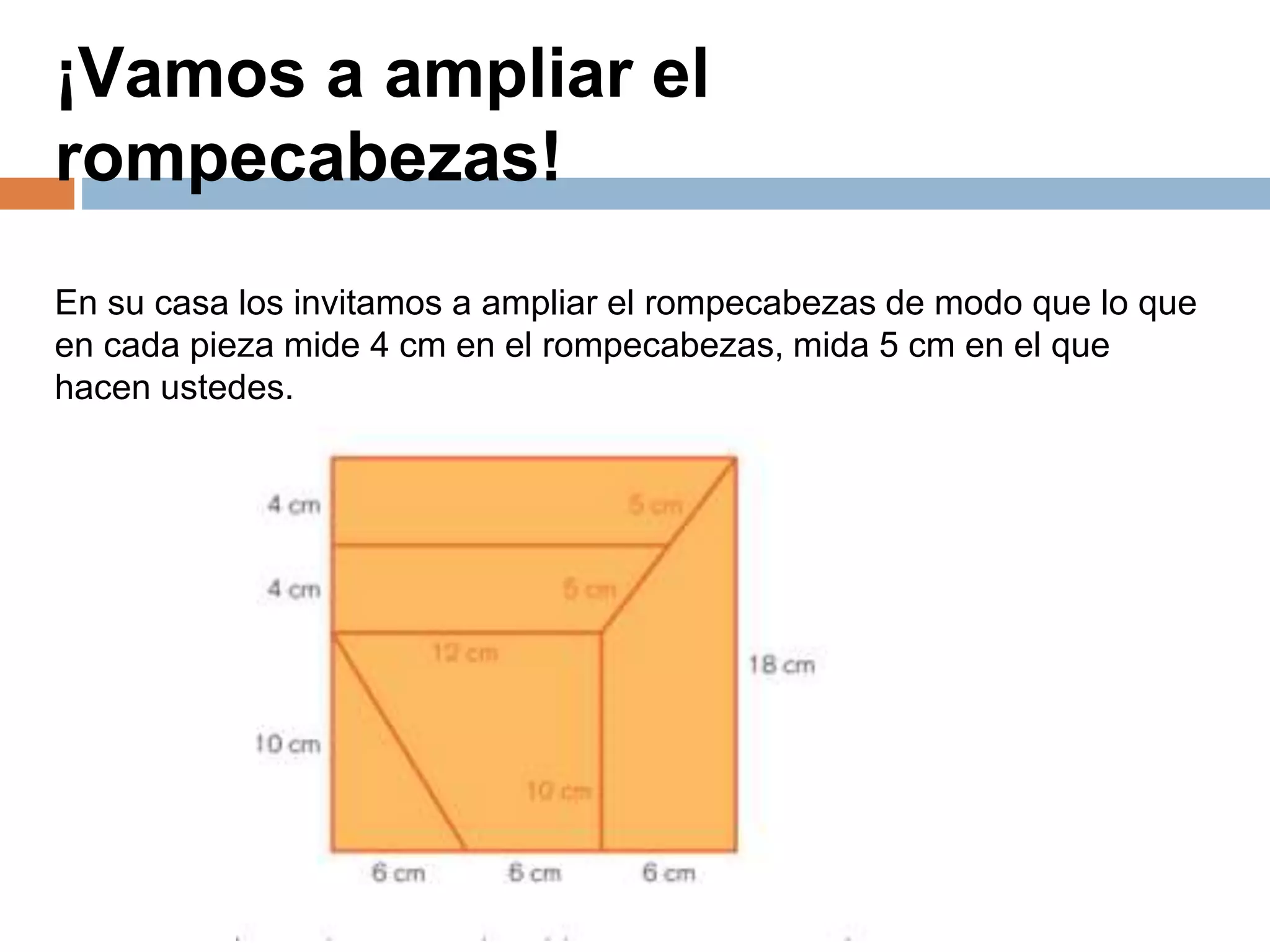
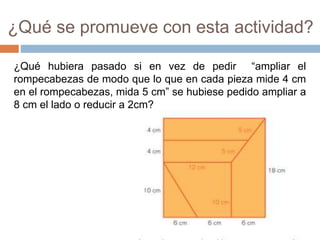
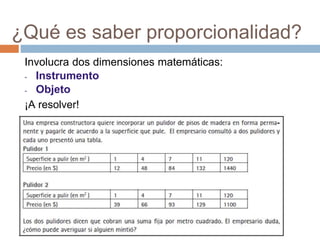
Este documento presenta información sobre la enseñanza de la proporcionalidad en la escuela primaria. Discute la importancia de este tema y cómo atraviesa diversos conceptos matemáticos. Explica brevemente las características de la proporcionalidad directa e inversa, y propone actividades para que los maestros exploren cómo se enseña este tema en los libros de texto y desarrollen material didáctico sobre proporcionalidad y sus aplicaciones.

1. ¡Vamos a ampliar el
rompecabezas!
En su casa los invitamos a ampliar el rompecabezas de modo que lo que
en cada pieza mide 4 cm en el rompecabezas, mida 5 cm en el que
hacen ustedes.

2. ¿Qué hubiera pasado si en vez de pedir “ampliar el
rompecabezas de modo que lo que en cada pieza mide 4 cm
en el rompecabezas, mida 5 cm” se hubiese pedido ampliar a
8 cm el lado o reducir a 2cm?
¿Qué se promueve con esta actividad?

3. PROPORCIONALIDAD
Un contenido Unificante

4. ¿Por qué enseñar proporcionalidad?
A lo largo de la biografía escolar de un estudiante la
proporcionalidad es un tema que se mantiene y casi
como ningún otro en su desarrollo confluyen diversas
nociones.
Por ejemplo:
- Los Números Racionales
- La Medida
- Las escalas
- Probabilidad
- Problemas de mezclas
- Porcentaje

5. ¿Qué conocemos de proporcionalidad?
En 5 min, responda de manera individual:
¿En mi trayectoria escolar qué me enseñaron de
proporcionalidad en la primaria?
Tenés algún libro cerquita tuyo para ver que se
enseña en la bibliografía de este tema…
búscalo y charlamos un poco más.

6. Construcción del sentido de la
Proporcionalidad
Finalizada la escuela primaria un estudiante
debería ser capaz de:
- Diferenciar situaciones de proporcionalidad directa e
inversa de las que no lo son, argumentando el porqué de
ello.
- Comparar situaciones de proporcionalidad en la que
intervienen un mismo tipo de magnitudes expresadas o
en distintas unidades.
- Articular las diferentes formas en que puede ser
representada una situación de proporcionalidad y
seleccionar la más adecuada en función del problema.

7. - Reconocer la fórmula y la gráfica cartesiana como
representaciones privilegiadas para analizar la
variabilidad y dependencia de las cantidades de
magnitudes involucradas en la relación de
proporcionalidad.
- Vincular el funcionamiento de las relaciones de
proporcionalidad en problemas de aritmética, de
medida, de funciones y de probabilidades.
- Identificar las definiciones y las propiedades
características y ponerlas en juego eficazmente en
función del problema a resolver.

8. Veamos que mencionan los NAP
Cuarto grado
Quinto grado

9. sexto grado

10. y los IPAP

11. ¿Qué es saber proporcionalidad?
Involucra dos dimensiones matemáticas:
- Instrumento
- Objeto
¡A resolver!

12. TEORICAMENTE…

13. Proporcionalidad directa
Una relación de correspondencia entre dos
variables es de proporcionalidad directa
cuando el cociente entre las cantidades que
se corresponden siempre es el mismo. A ese
cociente se lo llama CONSTANTE DE
PROPORCIONALIDAD DIRECTA

14. Propiedades de la Proporcionalidad
- Al multiplicar o dividir una de las cantidades
por un número, la cantidad correspondiente se
multiplica o divide por el mismo número y la
proporción se mantiene.
- Al sumar o restar dos valores de una de las
cantidades se obtiene un número
correspondiente con la suma o resta de los
valores correspondientes de la otra cantidad.

15. Otra representación de la PD
Las funciones son herramientas potentes para
modelizar situaciones en la que debemos
expresar una relación entre magnitudes.
f(x)
0 xEl estudio de la proporcionalidad desde una
perspectiva funcional implica hacer foco en la manera
en que varían las magnitudes involucradas, así como
en el dominio de validez de la relación

16. ¿Regla de tres simple?
¿La usamos?
La regla de tres es un método de resolución no es el
objeto matemático a enseñar, permite resolver
problemas de proporcionalidad pero no se la debería
determinar como la proporcionalidad en si misma.
¿Entonces la enseñamos?
Es otra estrategia para llegar a la solución pero es un
camino y no el único, es un algoritmo que tiene
muchos implícitos en su desarrollo.
Se puede abordar la proporcionalidad desde la
multiplicación y división dando sentido a los cálculos
teniendo en cuenta las propiedades.

17. Proporcionalidad Inversa
Si las cantidades de dos magnitudes
vinculadas entre sí varían de modo tal que su
producto permanece constante, decimos que
se trata de una relación de proporcionalidad
inversa
“Una se agranda y la otra se achica”

18. Propiedad de la
Proporcionalidad Inversa
-Al multiplicar una de las cantidades por un
número, la cantidad correspondiente se divide
por el mismo número y la proporción se
mantiene.
Por ejemplo:
Al doble de una cantidad, le corresponde la
mitad de la otra. Al triple de una cantidad, le
corresponde la tercera parte de la otra.

19. Estas actividades las proponemos para el
viernes 13 de noviembre 2020
Buscar en libros de 4°, 5°, y 6° (que pertenezcan a
una misma colección. ejemplo Estrada, Santillana
etc)
1) Investigue el discurso matemático escolar de
proporcionalidad. (Saque fotocopias o fotos que
muestren la secuencia)
2) Arme un esquema mental de los contenidos
relacionados con la proporcionalidad que se
debería trabajar en el aula de primaria.
3) En grupo de 5 personas armen un video con un
power point trabajando la proporcionalidad en
temas como Escala, Medida y Porcentaje. Deben
enviarlo por mail a las profesoras y luego ellas lo
subirán a la plataforma.