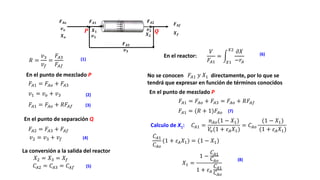
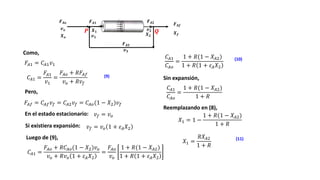
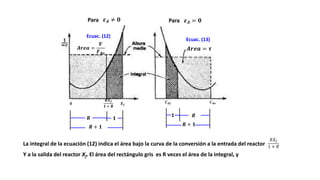
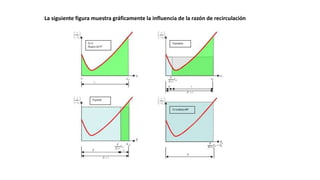
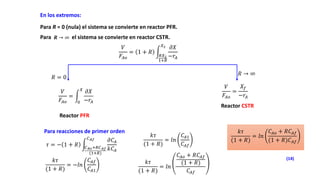
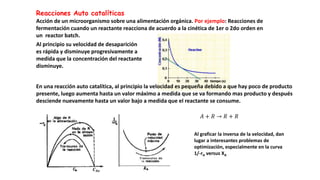
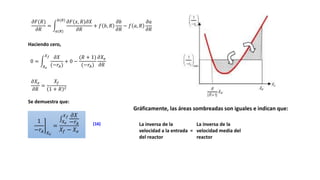
Este documento describe reactores de flujo pistón con recirculación (PFR), los cuales permiten aproximar el comportamiento de un reactor de mezcla completa (CSTR) utilizando un reactor PFR. Existen dos tipos de PFR con recirculación: uno con un simple punto de separación y otro con un separador CSTR. La recirculación permite mantener una operación casi isotérmica y promover selectividad. Se define la relación de recirculación R y se describen las ecuaciones que rigen este tipo de reactores para reacciones de primer y segundo orden