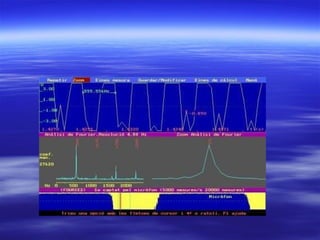
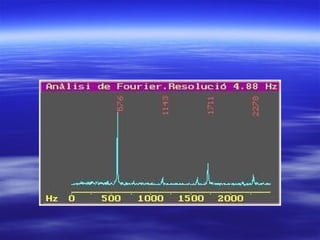
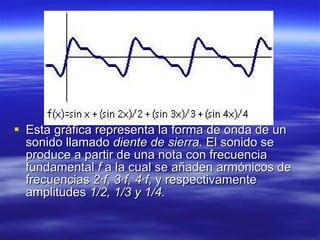
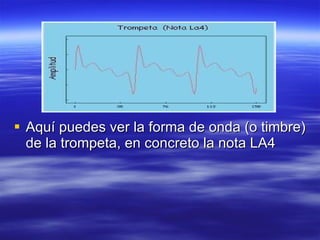
La resonancia ocurre cuando la frecuencia de excitación está cerca de la frecuencia natural de una estructura. La nota producida por una cuerda o tubo depende de factores como su longitud, tensión y grosor, y solo puede producir notas formadas por la onda fundamental y sus armónicos. El análisis de Fourier descompone cualquier señal periódica como una suma de funciones seno y coseno de frecuencias múltiplos de la frecuencia fundamental.

1. Resonancia

2. La resonancia es un estado de operación en el que una frecuencia de excitación se encuentra cerca de una frecuencia natural de la estructura de la máquina .

5. La onda producida por una cuerda vibrante De la misma forma que la longitud de un tubo es lo que determina la nota obtenida por este, en una cuerda vibrante influyen otros factores. La nota producida por una cuerda vendrá determinada por la longitud (L) , la tensión (T) , la densidad (d) y la sección (S) . Así, si disponemos de una cuerda muy tensa y fina, obtendremos una nota aguda; y por el contrario, si la cuerda está poco tensa y es gruesa, la nota será grave.

7. Esta sería la onda fundamental o primer armónico . La longitud de la onda es 2 veces la de la cuerda La frecuencia es f l = 2L f1

9. Si dividimos la cuerda en dos partes, la longitud de onda será igual a la longitud de la cuerda. Su frecuencia es 2 veces más grande que la anterior. Esta onda correspondería al segundo armónico El sonido sería una octava más alta que el fundamental

11. La longitud de onda es 2/3 de la longitud de la cuerda. Su frecuencia es 3 veces más grande que la primera. Esta onda correspondería al tercer armónico . Y es la quinta del segundo armónico.

13. La longitud de onda es 1/2 de la longitud de la cuerda. Su frecuencia es 4 veces más grande que la primera. Esta onda correspondería al cuarto armónico . El sonido sería dos octavas más arriba que el fundamental y la cuarta del tercer armónico.

14. La onda producida por un tubo cerrado. Un tubo cerrado con una longitud determinada sólo puede producir una nota, la cual estará formada por una onda fundamental y unos múltiplos de ésta, llamados armónicos. Estas ondas tienen que ser de tal forma que en la zona de máxima compresión del aire del tubo (la parte cerrada) haya un nodo y en la de mínima (la parte abierta), un vientre

16. Esta seria la onda fundamental o primer armónico . La longitud de la onda es 4 veces la del tubo La frecuencia es f=l/v

18. Esta seria la onda fundamental o primer armónico . La longitud de la onda es 4 veces la del tubo La frecuencia es f=l/v

20. La longitud de onda es 4/3 la del tubo Su frecuencia es 3 veces más grande que la anterior. Esta onda correspondería al segundo armónico .

22. La longitud de onda es 4/5 la del tubo. Su frecuencia es 5 veces más grande que la primera. Esta onda correspondería al tercer armónico .

23. Análisis de Fourier Nos hemos referido muchas veces en este apartado al análisis de Fourier. Utilizaremos la información que hemos obtenido de la ayuda que hay en el programa EXAO, para resumir en qué consiste este análisis. Joseph Fourier El siglo pasado, Joseph Fourier estableció el teorema matemático que lleva su nombre: cualquier función periódica se puede descomponer en suma de funciones seno y coseno. Las frecuencias de estas funciones son múltiplos, denominados armónicos, de un valor que se denomina frecuencia fundamental . Cada función está multiplicada por un coeficiente denominado coeficiente de la serie de Fourier. Evidentemente, una onda es una señal periódica que se puede analizar mediante la transformación de Fourier. Si se conocen los diferentes valores que definen la señal, no es necesario conocer la función matemática que los genera para determinar los armónicos presentes. Existen diferentes procedimientos matemáticos para calcular los coeficientes y las frecuencias; en cualquier caso, las operaciones matemáticas son numerosas y solo se pueden realizar, con cierta rapidez, con un ordenador. El resultado es el conocimiento de las frecuencias que caracterizan un timbre sonoro determinado a fin de poderlo reconocer o bien sintetizarlo.

27. El movimiento ondulatorio

28. Los armónicos son una serie de vibraciones subsidiarias que acompañan a una vibración primaria o fundamental del movimiento ondulatorio (especialmente en los instrumentos musicales).

29. Esta gráfica representa la forma de onda de un sonido llamado diente de sierra. El sonido se produce a partir de una nota con frecuencia fundamental f a la cual se añaden armónicos de frecuencias 2·f, 3·f, 4·f, y respectivamente amplitudes 1/2, 1/3 y 1/4.

30. Esta gráfica representa el sonido con forma de onda cuadrada. El sonido se produce a partir de una nota con frecuencia fundamental f a la cual se añaden armónicos de frecuencias 3·f, 5·f, 7·f, y respectivamente amplitudes 1/3, 1/5 y 1/7.

31. Aquí puedes ver la forma de onda (o timbre) de la trompeta, en concreto la nota LA4

32. Aquí puedes ver la forma de onda (o timbre) de una flauta, en concreto la nota DO4