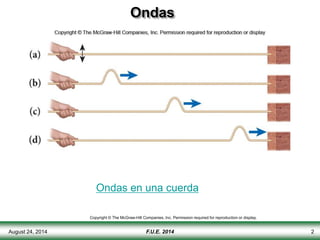
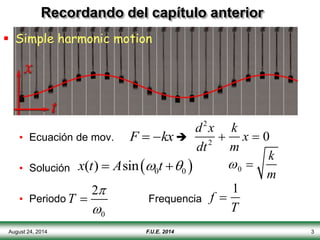
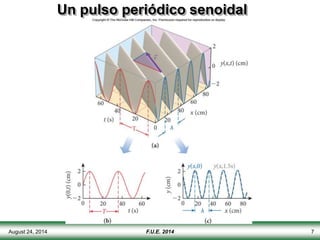
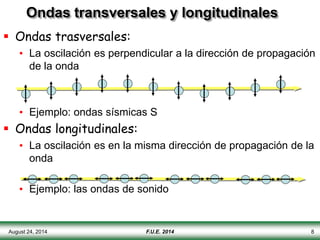
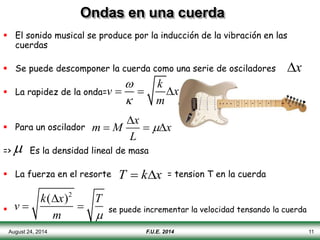
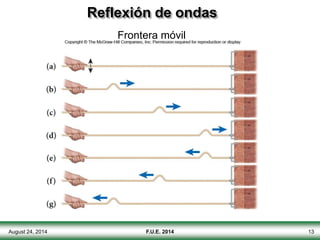
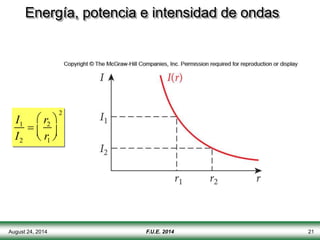
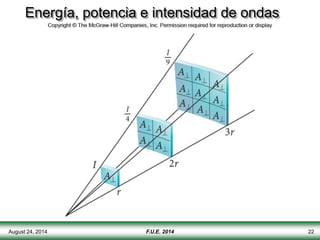
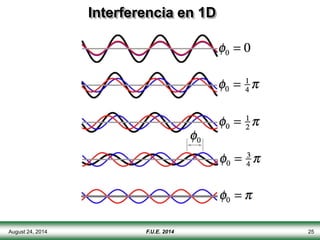
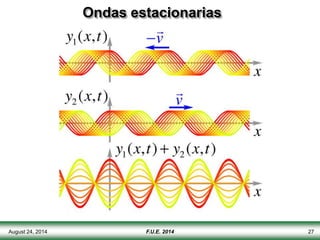
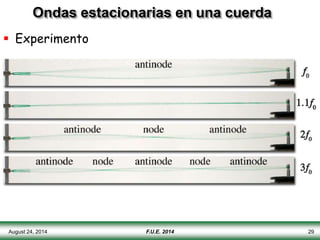
El documento describe las propiedades y tipos de ondas. Las ondas pueden ser mecánicas, electromagnéticas o de materia, y pueden ser transversales u longitudinales. Las ondas mecánicas requieren un medio para propagarse y transportan energía pero no materia. Las ondas en una cuerda se describen matemáticamente y se explican conceptos como interferencia, ondas estacionarias y frecuencias discretas.

1. August 24, 2014 1
Ondas
 Oscilación que se propaga a través
del tiempo y del espacio
 Las ondas trasportan energía a
través del espacio
 Pero usualmente no trasportan
materia.
 Para una serie de oscialdores
acoplados.
 Las oscilaciones se propagan, no los
osciladores.
 Las ondas pueden “interferir” unas
con otras y crear patrones de
interferencia.
Copyright © The McGraw-Hill Companies, Inc. Permission required for reproduction or display.
F.U.E. 2014

2. August 24, 2014 2
Ondas
Copyright © The McGraw-Hill Companies, Inc. Permission required for reproduction or display.
Ondas en una cuerda
F.U.E. 2014

3. August 24, 2014 3
Recordando del capítulo anterior
 Simple harmonic motion
• Ecuación de mov. 
• Solución
• Periodo Frequencia
d2
x
dt2

k
m
x  0
 0 0( ) sinx t A t  
F  kx
0 
k
m
0
2
T


 f 
1
T
F.U.E. 2014

4. August 24, 2014 4
Ondas
 Lanzando una piedra en un
estanque se puede observar un
patrón circular de crestas que se
mueven hacia afuera
• Las ondas se mueven hacia afuera
formando circulos concéntricos.
• Los objetos que están en el estanque
permanecen en el mismo lugar, solo se
mueven hacia arriba y hacia abajo
cuando son alcanzados por las crestas
de las ondas.
 Hay tres tipos de ondas:
• Mecánicas: sonido, ondas sísmicas,
ondas en cuerdas. Requieren de un
medio para su propagación.
• Electromagnéticas: radio, microondas
X rayos X, etc… Se propagan en el
vacío
• Materia: Física cuántica…
F.U.E. 2014

5. August 24, 2014 5
“La Ola”
Olas en el estadio
Parlante en bomba de vacío
F.U.E. 2014

6. August 24, 2014 6
Un pulso periódico senoidal
 Hasta el momento solo hemos visto un pulso en una onda
 Ahora usaremos una exitación senoidal periodica de
frecuencia:
f = 1/T.
 Esta onda viajará con velocidad constante por el medio
 La distancia entre dos máximos consecutivos se llama
longitud de onda, 
 Durante un periodo la onda avanza una longitud de onda
 La rapidez de la onda es:
v 

T
 v   f
F.U.E. 2014

7. August 24, 2014 7
Un pulso periódico senoidal
F.U.E. 2014

8. August 24, 2014 F.U.E. 2014 8
Ondas transversales y longitudinales
 Ondas trasversales:
• La oscilación es perpendicular a la dirección de propagación
de la onda
• Ejemplo: ondas sísmicas S
 Ondas longitudinales:
• La oscilación es en la misma dirección de propagación de la
onda
• Ejemplo: las ondas de sonido

9. Ondas transversales y longitudinales
August 24, 2014 F.U.E. 2014 9
Longitudinal
Transversal

10. August 24, 2014 10
Descripción matemática de las ondas
F.U.E. 2014

11. August 24, 2014 11
Ondas en una cuerda
 El sonido musical se produce por la inducción de la vibración en las
cuerdas
 Se puede descomponer la cuerda como una serie de osciladores
 La rapidez de la onda=
 Para un oscilador
=> Es la densidad lineal de masa
 La fuerza en el resorte = tension T en la cuerda
 se puede incrementar la velocidad tensando la cuerda
x
k
v x
m


  
x
m M x
L


  

T  kx
v 
k(x)2
m

T

F.U.E. 2014

12. August 24, 2014 F.U.E. 2014 12
Reflexión de ondas
Frontera fija

13. August 24, 2014 F.U.E. 2014 13
Reflexión de ondas
Frontera móvil

14. August 24, 2014 14
Ondas planas
 Lejos de la fuente puntual los ángulos entre rayos
se hacen pequeños
 Todos los rayos son paralelos
 => Ondas planas
 Igual descripción matemática.
Que ondas en 1D
 La amplitud varía muy poco al alejarse de la fuente.
En el límite: Amplitud constante
 0( , ) siny r t A x t    
r
F.U.E. 2014

15. August 24, 2014 15
Ondas en 2D
 0( , ) sin
A
y r t r t
r
    
r
F.U.E. 2014

16. Problemas
15.25: Una onda senoidal propagándose en la
dirección +x tiene una longitud de onda de 15 cm, una
frecuencia de 10 Hz y una amplitud de 10 cm. La parte
de la onda que está en el origen en t = 0 tiene un
desplazamiento vertical de 5 cm. Para esta onda
determine: a) el número de onda,b) el periodo, c) la
frecuencia angular, d) la rapidez, e) el ángulo de fase,
f) la ecuación de la onda.
August 24, 2014 F.U.E. 2014 16

17. Problemas
15.27 El punto A en la figura está 30 cm debajo del
techo. Determine cuanto tiempo más tardará un
pulso de onda para viajar a lo largo del alambre 1
que a lo largo del alambre 2.
August 24, 2014 F.U.E. 2014 17

18. Problemas
15.28 Una determina cuerda de acero de una guitarra
eléctrica tiene una densidad lineal de masa de
1.93 g/m. Si la tensión el la cuerda es de 62.2 N
determine la rapidez de las ondas en la cuerda.
¿Cuánto se debe cambiar la tensión para para
incrementar la rapidez de las ondas un 1%?
August 24, 2014 F.U.E. 2014 18

19. Problemas
12.30 Un alambre de densidad de masa lineal uniforme
está suspendido del techo. Tarda 1 s para que al
pulso recorra el largo del alambre. Determine la
longitud del alambre.
August 24, 2014 F.U.E. 2014 19

20. August 24, 2014 F.U.E. 2014 20
Energía, potencia e intensidad de ondas

21. August 24, 2014 F.U.E. 2014 21
Energía, potencia e intensidad de ondas
I1
I2

r2
r1




2

22. August 24, 2014 F.U.E. 2014 22
Energía, potencia e intensidad de ondas

23. August 24, 2014 F.U.E. 2014 23
Superposición e interferencia
 La ecuación de onda es lineal
=> La función “Y” solo se expresa como la primera
potencia de la ecuación.
 Suponga que se tienen dos soluciones para la
ecuación de onda, entonces una combinación lineal
de las dos ecfuaciones es la solución
 Caso especial – Principio de superposición:
“Dos o más soluciones para la ecuación de onda
pueden ser sumadas para obtener otra solución de
onda”
y(x,t)  ay1(x,t)  by2 (x,t)
y(x,t)  y1(x,t)  y2 (x,t)

24. August 24, 2014 F.U.E. 2014 24
Interfencia en 1D
 Consecuencias del principio de superposición para
dos ondas senoidales.
 Primero: Dos ondas con idéntica amplitud, número
de onda y frecuencia angular pero diferente ángulo
de fase.
 Para diferentes ángulos de fase se tienen
diferentes patrones de interferencia
y(x,t)  Asin(x t)  Asin(x t 0 )

25. August 24, 2014 F.U.E. 2014 25
Interferencia en 1D

26. August 24, 2014 F.U.E. 2014 26
 Un caso muy especial del principio de superposición
en el que se presenta cuando se tienen dos ondas
idénticas, con igual fase pero diferente velocidad
de propagación
 Utilizando la identidad trigonométrica
 Resulta:
 Una onda con nodos y antinodos en puntos
específicos de la coordenada espacial.
Ondas estacionarias
y(x,t)  y1(x,t)  y2 (x,t)
 Asin( x  t)  Asin( x  t)
y(x,t)  2Asin(x)cos(t)
sin(  )  sin cos  cossin

27. August 24, 2014 F.U.E. 2014 27
Ondas estacionarias

28. August 24, 2014 F.U.E. 2014 28
Ondas estacionarias
video

29. August 24, 2014 F.U.E. 2014 29
Ondas estacionarias en una cuerda
 Experimento

30. August 24, 2014 F.U.E. 2014 30
Longitudes de onda discretas
 Posibles longitudes de onda
 La más baja, n=1: fundamental,
= primer armónico
 n=2: segundo armónico, …
n
n
2
 L, n  1,2,3,...
n 
2L
n
, n  1,2,3,...

31. August 24, 2014 F.U.E. 2014 31
Frecuencias
 La relación entre la longitud de onda y la frecuencia
es
 Las posibles frecuencias son:
 Utilizando la expresión para la rapidez en una
cuerda:
v   f
fn 
v
n
 n
v
2L
, n  1,2,3,...
fn 
v
n
 n
T
2L 
 n
T
4Lm
, n  1,2,3,...

32. Problemas
15.36 Una onda senoidal en una cuerda se describe
por la ecuación:
y= (0.1 m) sen (0.75x-40t)
donde “x” y “Y” están en metros y t en segundos. Si
la densidad lineal de masa de la cuerda es de 10
g/m, determine: a) el ángulo de fase, b) la fase de
la onda en x = 2 cm y t = 0.1 s, c) la rapidez de la
onda, d) la longitud de onda, e) la frecuencia, f) la
potencia transmitida por la onda.
August 24, 2014 F.U.E. 2014 32

33. Problemas
15.37 En un experimento acústico, una cerda de piano
con una masa de 5 g y una longitud de 70 cm se
mantiene bajo tensión al tender la cuerda a través
de una polea sin fricción y suspender de ella un peso
de 250 kg. El sistema completo se coloca en un
ascensor. Determine: a) la frecuencia fundamental
cuando el ascensor está en reposo, b) la magnitud y
dirección de la aceleración del ascensor para que la
cuerda produzca una frecuencia de 440 Hz.
August 24, 2014 F.U.E. 2014 33

34. Problemas
15.41 Una cuerda de 3 m de largo, sujetada a ambos
extremos tiene una masa de 6 g. Si se quiere
establecer una onda estacionaria en esta cuerda
con una frecuencia de 300 Hz y tres antinodos,
determine la tensión a la que se debe mantener la
cuerda.
August 24, 2014 F.U.E. 2014 34

35. Problemas
15.42 Un vaquero camina al ritmo de
aproximadamente dos pasos por segundo,
sosteniendo un vaso de un diámetro de 10 cm que
contiene leche. La leche se agita y sube cana vez
más en le vaso hasta que empieza finalmente a
rebosar. Determine la rapidez máxima de las ondas
en la leche.
August 24, 2014 F.U.E. 2014 35

36. Problemas
15.58 La tensión en un cable de acero de 2.7 m de
largo y 1 cm de diámetro (ρ = 7800 kg/m2) es de
840 N. Determine la frecuencia central de
vibración del cable.
August 24, 2014 F.U.E. 2014 36