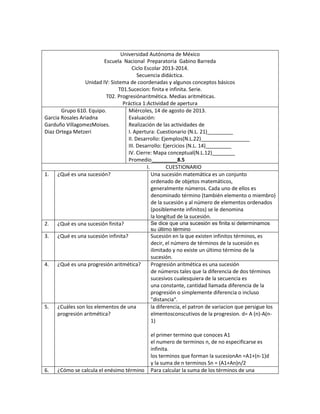
Este documento presenta las actividades realizadas por un grupo de estudiantes como parte de una unidad sobre sucesiones, series, progresiones aritméticas y medias aritméticas. Incluye cuatro actividades: 1) un cuestionario sobre estos conceptos, 2) ejemplos ilustrativos, 3) ejercicios prácticos y 4) un mapa conceptual de resumen. El grupo obtuvo un promedio de 8.5 después de completar las actividades.