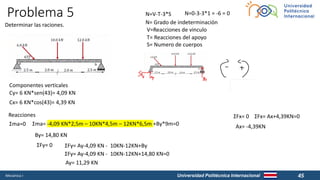
El documento trata sobre conceptos básicos de mecánica como centro de masa, centroide, momentos de inercia y cargas distribuidas. Explica cómo calcular el centroide de diferentes figuras geométricas y cómo determinar las reacciones en vigas sometidas a cargas distribuidas y concentradas. También cubre temas como fuerzas sobre superficies sumergidas y cómo calcular la presión ejercida por un bloque de agua contenido por un dique.