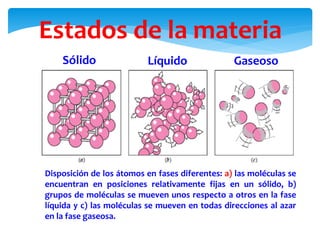
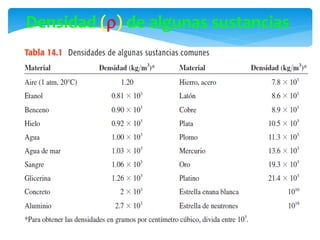
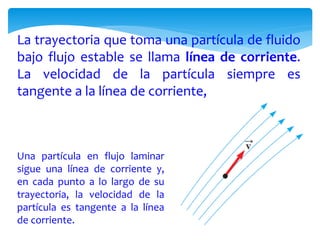
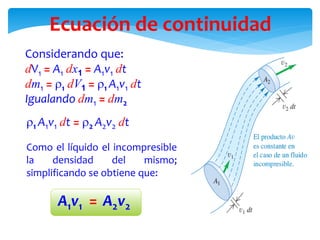
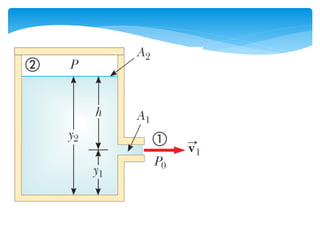
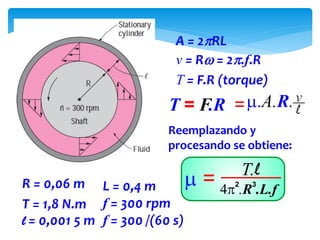
Este documento presenta conceptos básicos de hidrodinámica. Introduce la mecánica de fluidos y define un fluido como una sustancia que puede cambiar fácilmente de forma. Explica los estados de la materia sólido, líquido y gaseoso. Luego define densidad y proporciona ejemplos. Finalmente, introduce conceptos clave como caudal, ecuación de continuidad y ecuación de Bernoulli para analizar el flujo de fluidos.